物理系统是游戏引擎中最重要的逻辑系统,也是游戏引擎中极为复杂和庞大的系统,物理决定了游戏世界是否符合人对真实世界的认知,好的物理系统能让游戏可玩性大幅提升,这一节来简单了解游戏引擎中的物理系统和简单的碰撞检测思路。因为物理系统非常复杂,因此我们先学习基础的概念和思想,之后如果有必要会在专门的物理专题中进一步学习详细的算法和实现。
1 物理系统的基本概念
在游戏引擎中,物理世界和玩家看到的游戏世界是有一定区别的,渲染和动画是为了让物理世界以更酷炫的方式呈现在玩家面前,而整个游戏世界的运行可能是像下图中右边的样子:

游戏世界中的所有物体在物理世界中都被称为 Actor,Actor 通常都是一些简单的几何形状,而不是精细的模型,Actor 具体分为几种类型,首先是静态的 Actor,也就是静止不动的物体,比如墙体:

还有动态的 Actor,比如角色和 NPC:
还有一类特殊的 Actor 叫做触发器(Trigger),比如我们走到某个位置,门就会自动打开,或者老头环中升降梯的触发方块;最后还有一些 Actor 可能不符合现实世界的运动规律,但却是游戏性需要的,这类 Actor 称为 Kinematic。
这些 Actor 的形状一般都非常简单,因为物理系统需要计算物体之间的碰撞和力的作用,复杂的模型是不便于计算的,因此 Actor 一般都是球体、胶囊体、立方体等,复杂一点的还有不规则凸面体和三角形片面等:
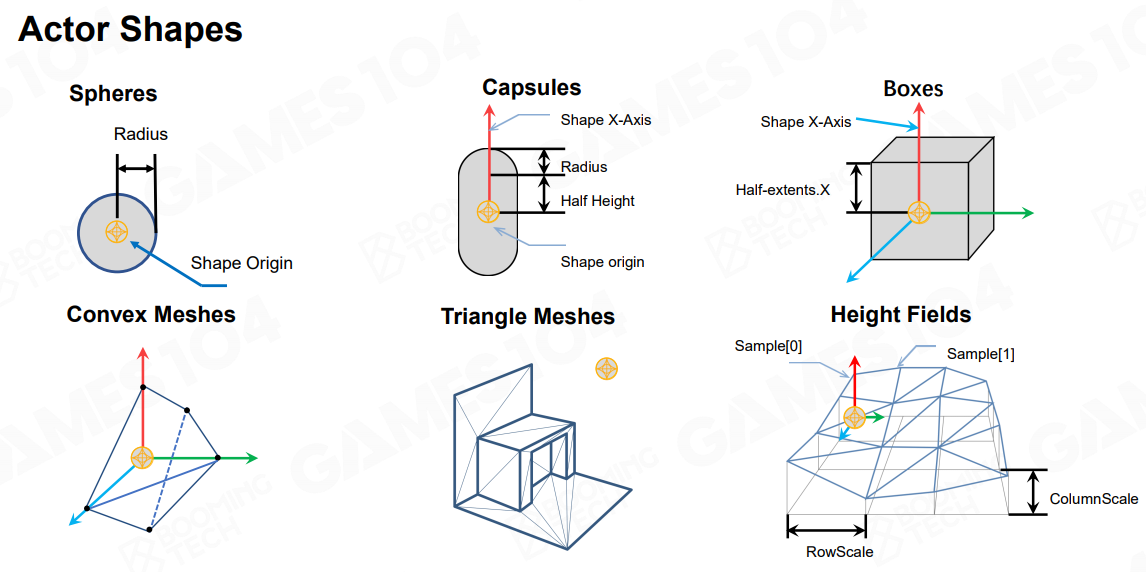
一般来说游戏中比较小的物体都会用球体,而角色用胶囊体,房屋和箱子或者墙面就使用立方体,其他比较复杂的需要相对比较精细计算的物体才使用凸包等。


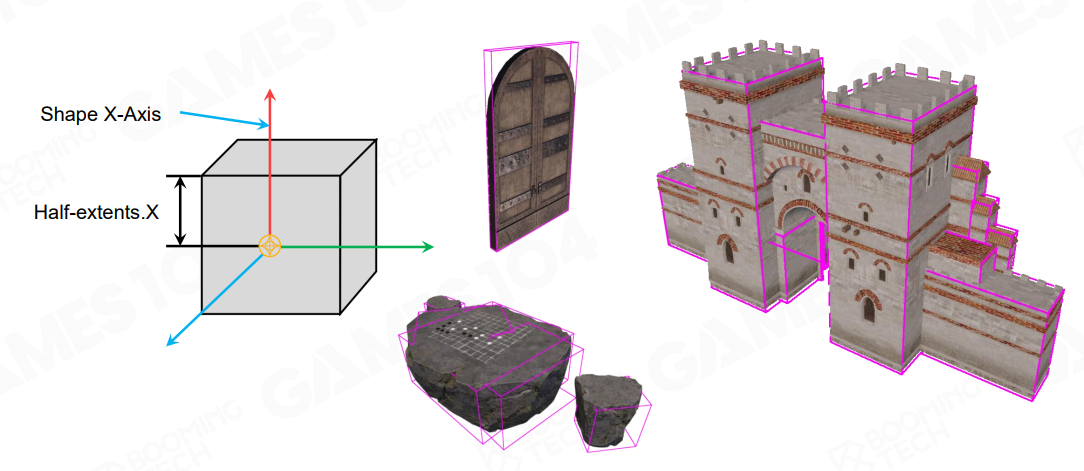
对于每一个 Actor,要进行物理计算,就需要有他们的 Shape 以及重心,还有其他物理材质属性,比如摩擦系数、弹力系数等等。
2 物理模拟
物理模拟最重要的就是模拟物体在不同力作用下的运动,由于游戏中几乎不存在规则运动,因为各种力是与游戏交互息息相关的,在游戏运行之前我们不知道这些力会是什么样,因此也没有办法建立解析的物理运动模型,比如标准的圆周运动等,于是就需要根据物体当前的运动状态和力的作用,模拟物体的运动。
对于真实世界理想的运动,在任何时间根据位置就可以通过求导就算出速度:
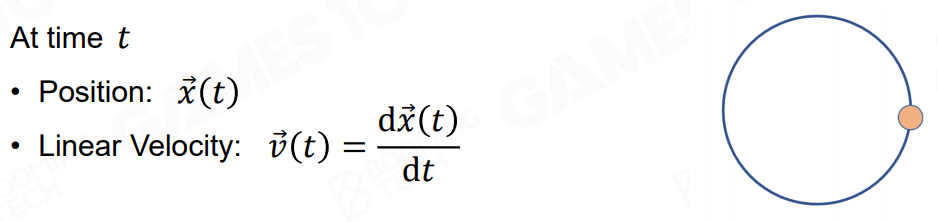
但游戏世界我们不知道物体是怎样运动的,我们知道的只有物体在当前时刻的位置和速度,要以此来估算下一时刻的位置和速度,从而模拟物体的真实运动:
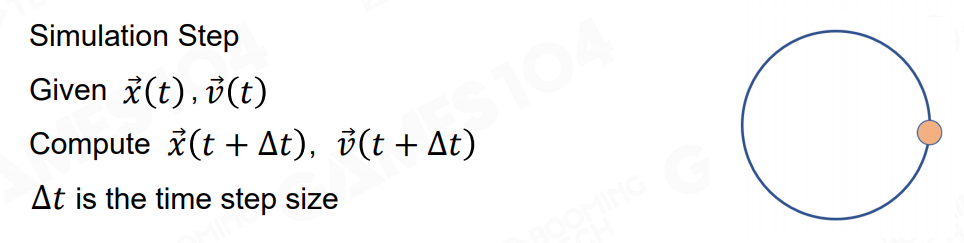
从数学上严格的来计算,下一时刻物体的位置应该是从当前时刻到下一时刻速度的积分加上当前位置:
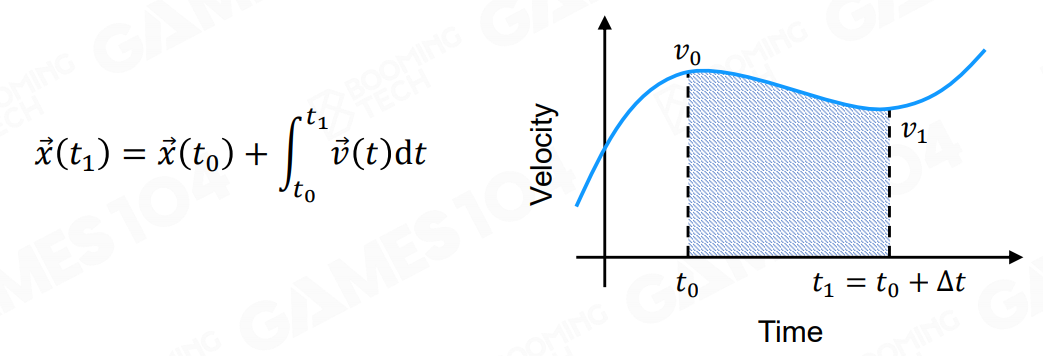
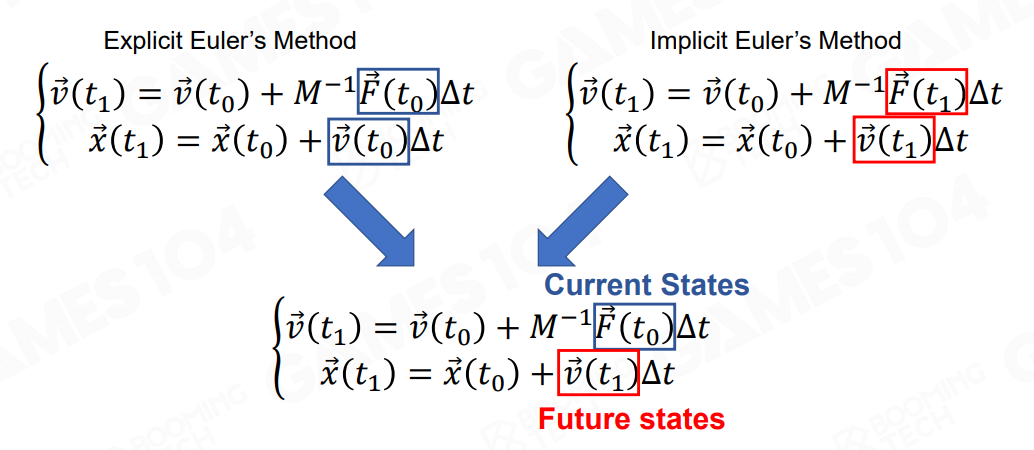
但我们不知道下一时刻的速度和这之间速度的变化,所以要去进行估算,显式欧拉积分的思想是利用当前时刻的力估计下一时刻的速度,然后用当前时刻的速度估算下一时刻的位置:

但这样的问题是会使得模拟出的轨迹向外偏离,因为我们用的是当前时刻的力进行的估计,而对于圆周运动当前时刻的力肯定要比下一时刻的力的方向向外:
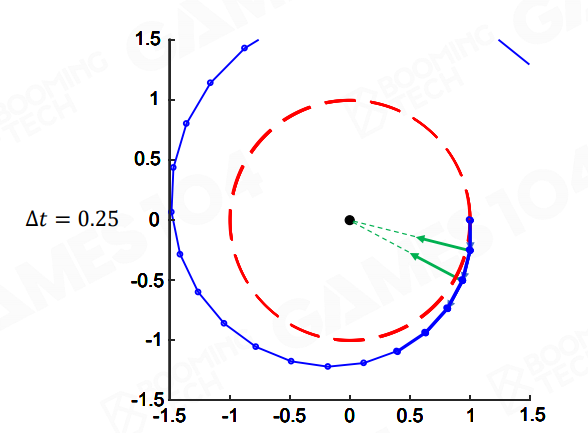
由此也说明显式欧拉积分是不稳定的,很难收敛,除非步长非常小,但那样又会增大计算量,不过好处是计算简单。
另一种隐式欧拉积分正好相反,假设我们已知下一时刻的力和速度,来反向逼近结果:
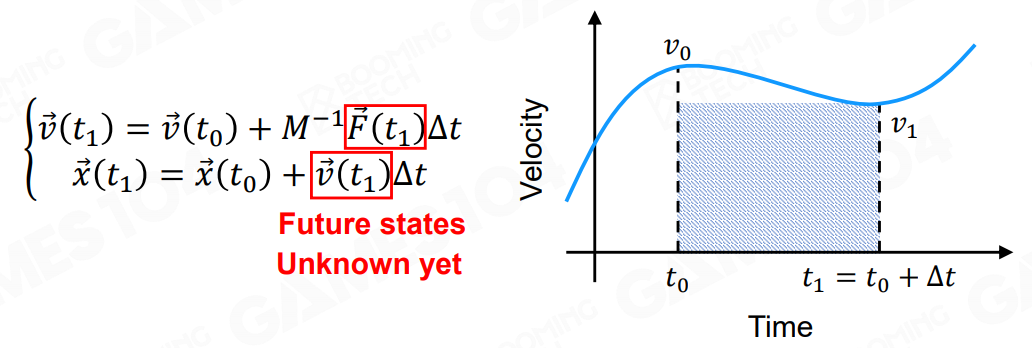
这样做相比于显式积分更加稳定,但求解也更困难。
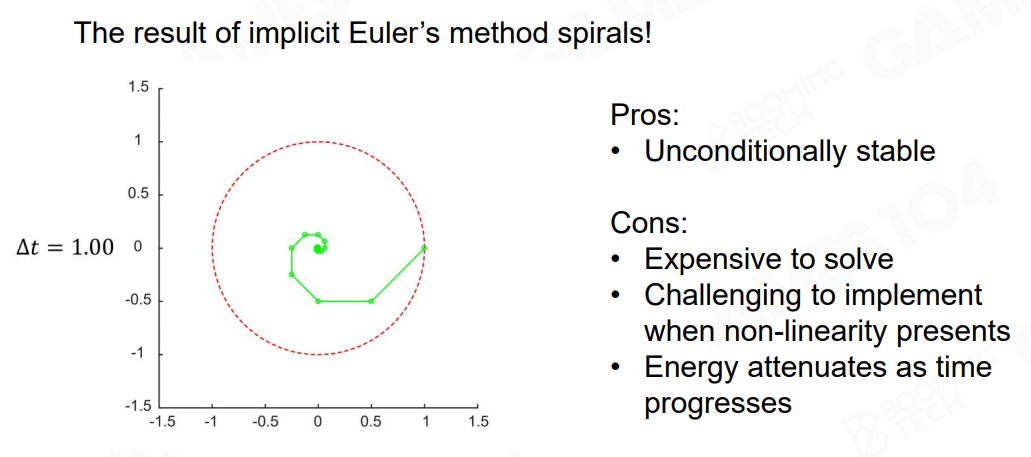
物理引擎中一般使用半隐式欧拉积分,即使用当前时刻的力估计下一时刻的速度,再用下一时刻的速度估计下一时刻的位置,相当于结合了显式和隐式:
这样的方法被证明是稳定的,而且模拟结果非常好,并且易于计算。
当然在游戏中,物体不是一个质点,是有体积的,收到力的作用后,物体的运动也不仅仅是在世界空间的运动,还包含物体本身的旋转等运动,因此还涉及到刚体动力学的许多知识,这里就不展开了。
3 碰撞检测
碰撞检测一般分为两个阶段,首先是粗检测,利用 AABB 来进行初步检测,判断物体是否相交,如果相交再进行精细的计算二者的相交位置,深度等。
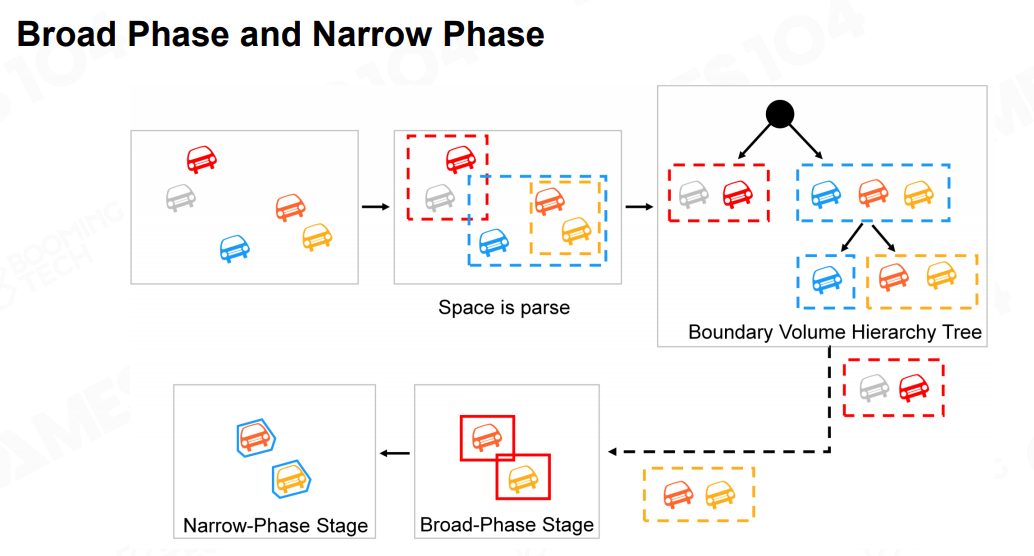

3.1 粗检测阶段
粗检测阶段一般可以利用 BVH,类似于渲染中的视锥体剔除,但更好的方法是 Sort and Sweep 方法,分为两个阶段:
首先是 Sort 阶段,对场景中所有的 AABB 的边界在不同维度上进行排序,从而可以轻松的判断是否相交,类似于判断重复区间:
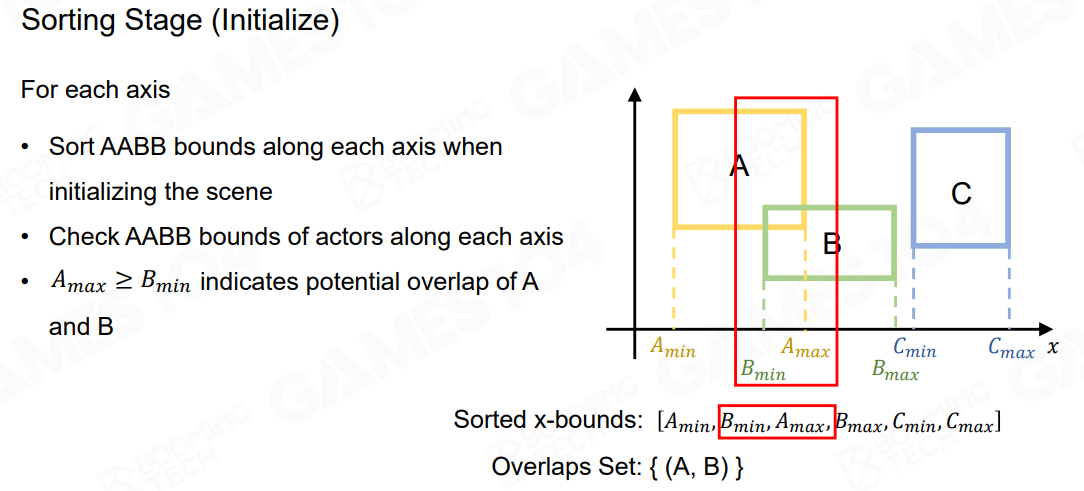
由于场景中大部分物体的位置都是固定不变的,因此一旦排好序之后,只需要调整移动的物体在排序中的位置即可,而对于一个有序数组,调整某些元素的位置是很快的,这就是第二个 Sweep 阶段:
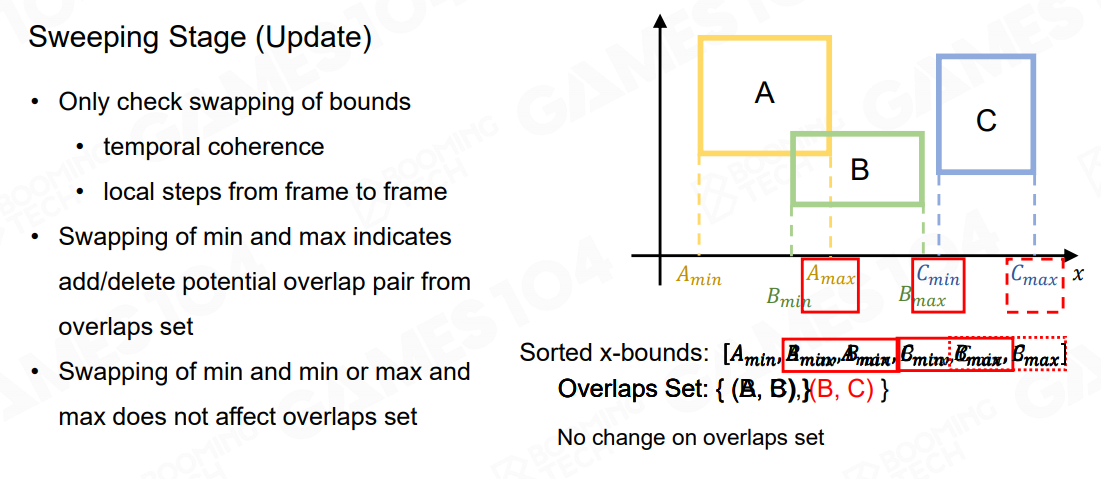
3.2 精细检测阶段
经过粗检测之后就要具体求解交点深度、位置和朝向等信息,从而施加碰撞力了,这部分求交相对比较困难,对于简单形体的 Actor 来说还比较简单,比如球体之间的求交或者胶囊体的求交:
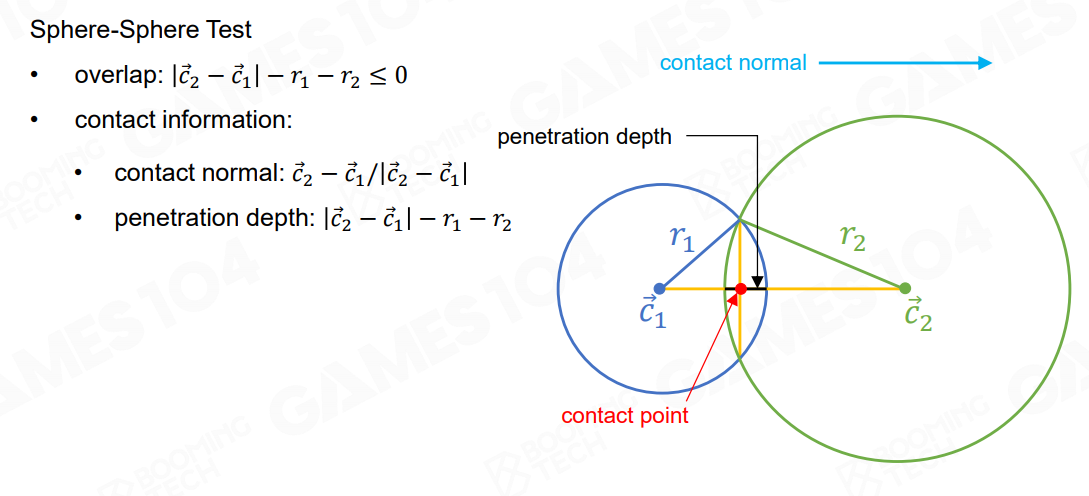


但对于凸多面体就比较困难了,这里简单了解两个算法的思路,这两个算法不仅适用于碰撞检测,还适用于其它系统。
3.2.1 Minkowski Difference-based Methods
明可夫斯基和是集合论中的概念,两个集合的明可夫斯基和定义为集合中全部元素两两相加形成的新的集合:

对于几何中的点集来说,如果是一个无穷点集 B,比如三角形覆盖的点和一个点 A 的明可夫斯基和表示的就是点集 B 中的所有点加上点 A 所形成的新的三角形覆盖的所有点:
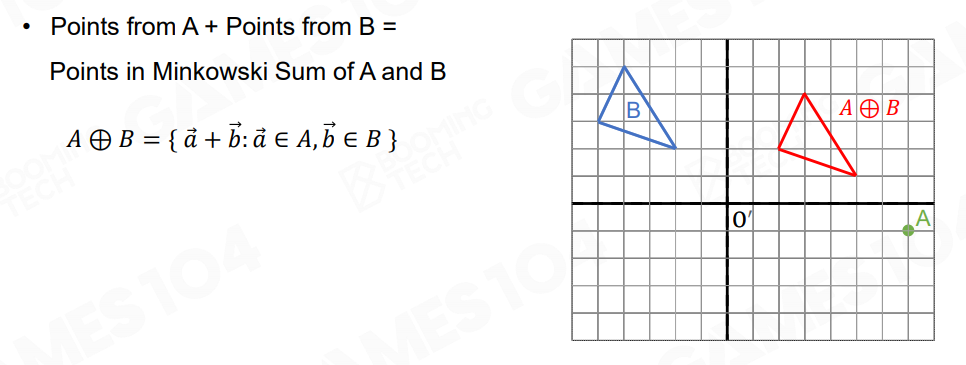
而一个无穷点集 B 和一条线段 A 的明可夫斯基和表示的就是点集 B 中的所有点在线段 A 方向上进行移动,所形成的新的多边形覆盖的所有点:
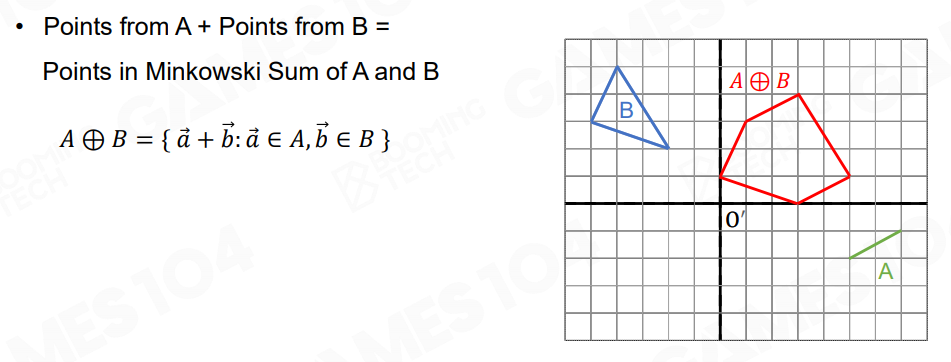
同理,一个无穷点集 B 和另一个无穷点集 A 的明可夫斯基和表示的就是点集 B 中的所有点在 A 各个边方向上进行移动,所形成的新的多边形覆盖的所有点:
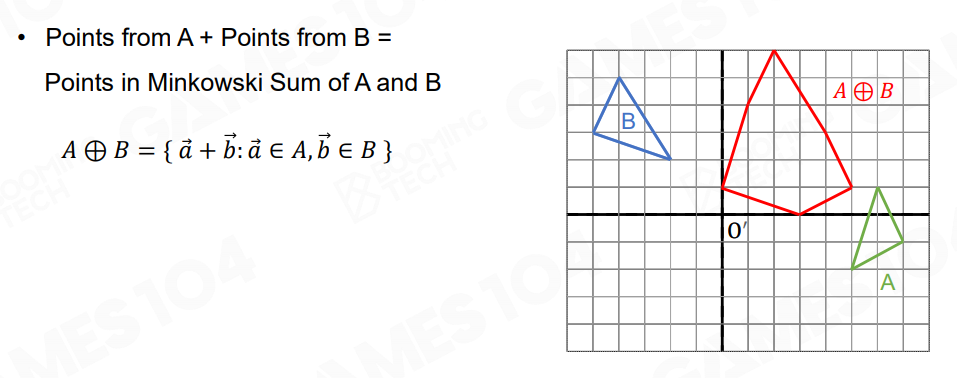
也就是两个凸多边形的明可夫斯基和会形成一个新的凸多边形。并且这个新的凸多边形实际上就是两个凸多边形所有顶点之和所对应的点的凸包:
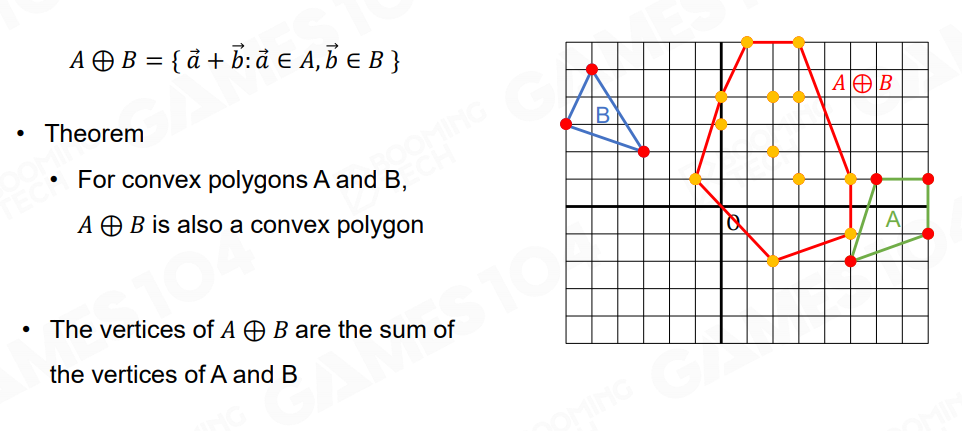
有了加法自然可以定义减法,将一个点集中的所有点取反再相加即可:
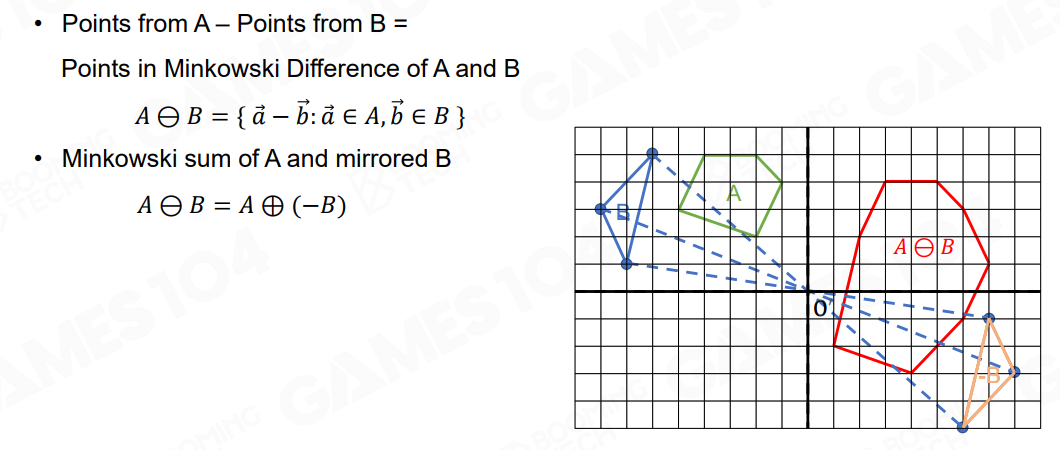
于是当两个凸多边形有交点的时候,他们的明可夫斯基差形成的凸多边形一定会过原点:
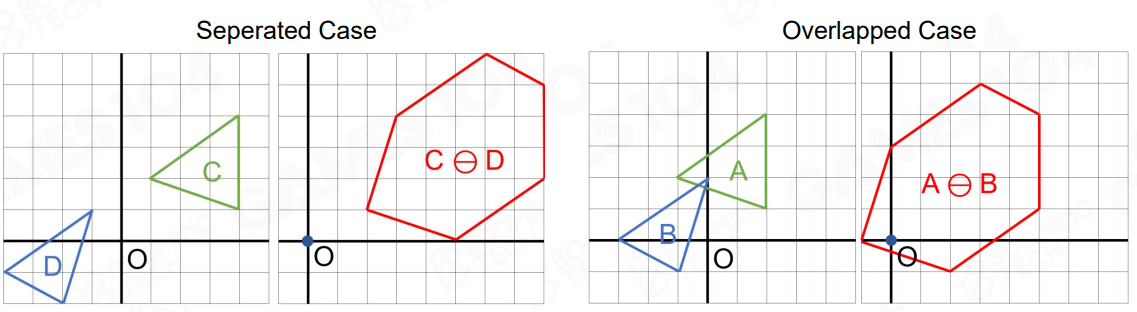
由此可以判断二者是否相交,并且可以求出相交的具体深度、位置等属性。至于如何快速判断凸多边形过原点,一个著名的方法是 GJK 算法,是通过迭代不断逼近原点的方法,这里不展开。
3.2.2 Separating Axis Theorem (SAT)
分离轴算法也是常用的凸多面体求交算法,二维情况下如果两个凸多边形没有交点,那么一定存在一个轴可以使得;两个多边形的顶点分列两侧:
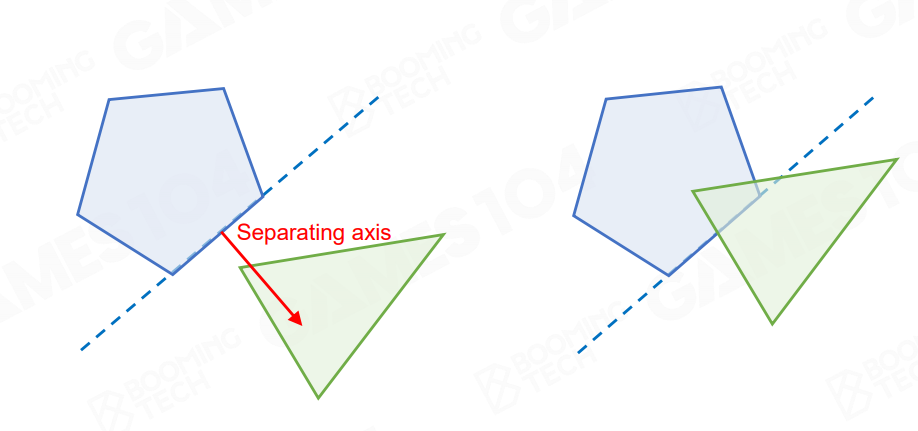
于是遍历多边形的每条边作为轴,判断顶点和直线关系,如果存在任何一条轴能把两个多边形的顶点完全分开就说明二者没有交点,三维中的情况更加复杂一些,这里也不再赘述了。
碰撞检测结束后,还要根据算出来的碰撞点、力的朝向等对碰撞的物体做出响应,最简单的就是分别给物体一个力让他们分开,具体如何计算也不展开了,之后如果有必要,会在物理专题中详细学习。