在离线渲染中,基于物理的渲染可以带来非常真实效果,基于物理的渲染方法的核心就是各种基于物理的材质,这些材质的 BRDF 相对于Blinn Phong 等基于经验的材质模型会比较复杂,因此处理起来也比较费时,不适用于实时渲染,这一节主要学习实时渲染中如何处理基于物理的材质。
1 再谈微表面
通过之前的学习可以发现,实时渲染的各种方法实际上都是在离线渲染的基础上,做各种假设和近似来快速得到一个近似地效果,材质也不例外,基于物理的材质最常用的就是微表面模型,实时渲染中同样使用微表面模型,因此我们首先来回顾微表面模型的内容。
微表面 BRDF 由菲涅尔项 F,几何项 G 和法线分布函数 D 组成,描述了从某个入射方向来的光会向某个出射方向反射出多少能量:
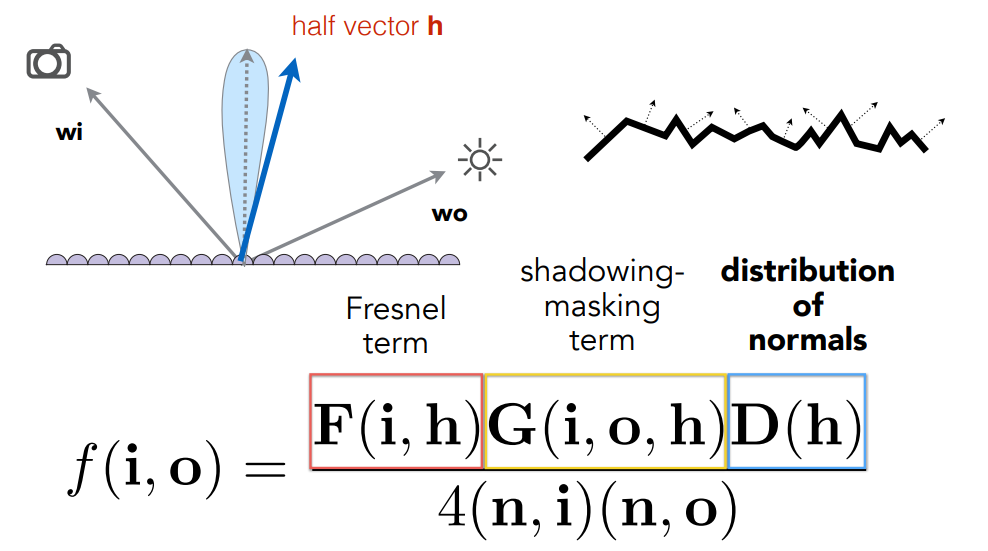
1.1 菲涅尔项
菲涅尔项描述了随着入射方向和法线夹角增大,反射会变得越来越强的现象:
对于非导体,入射方向与法线夹角和反射率的关系为: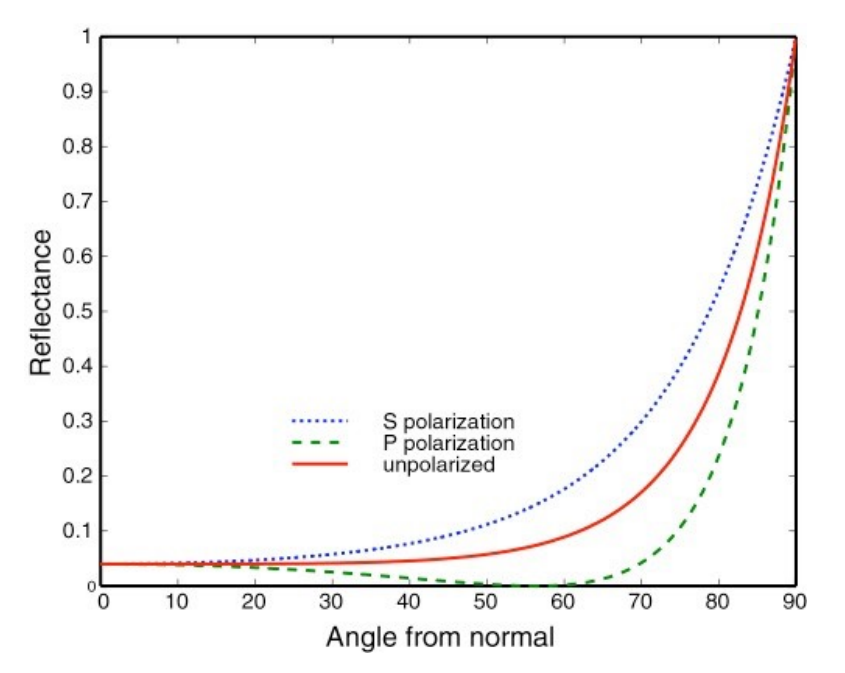
即当我们沿着法线方向观察的时候几乎不会看到反射,而当我们垂直于法线方向观察的时候会看到物体几乎全部被反射。
对于导体(金属),菲涅尔曲线为:
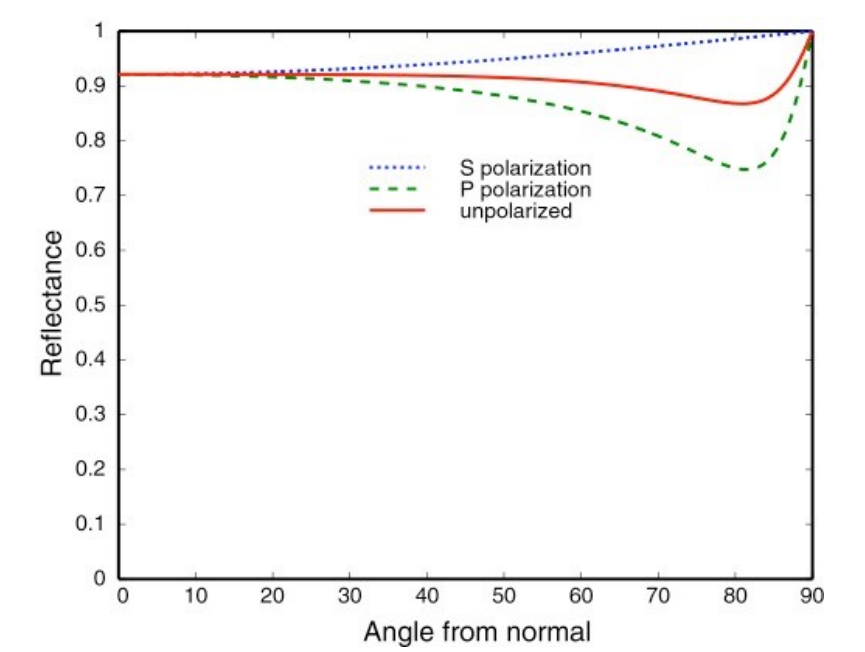
即导体本身就会发生强烈的反射,随着视角变化,观察到的反射不会有太大的变化,因此可以说金属本身就会有比较固定的颜色(反射率),比如金、银、铜都有自己的颜色。
菲涅尔项表达式非常复杂,与介质和材质的折射率有关,一般在渲染中使用 Schlick’s 近似:

总的来说,菲涅尔项描述了对于给定的入射方向和出射方向(半程向量),会有多少光从入射方向反射到出射方向上,一般来说渲染的时候出射方向固定,就是观察方向,那么不同入射方向的光反射到观察方向上的比例就不同,这是菲涅尔项的意义。
1.2 法线分布函数
法线分布函数描述了物体表面有多少微表面的法线和给定的半程向量方向一致,那么这些微表面才会被看到(只考虑镜面反射)。这是一个宏观的理解,实际上 NDF 描述的就是微表面的法线的概率分布: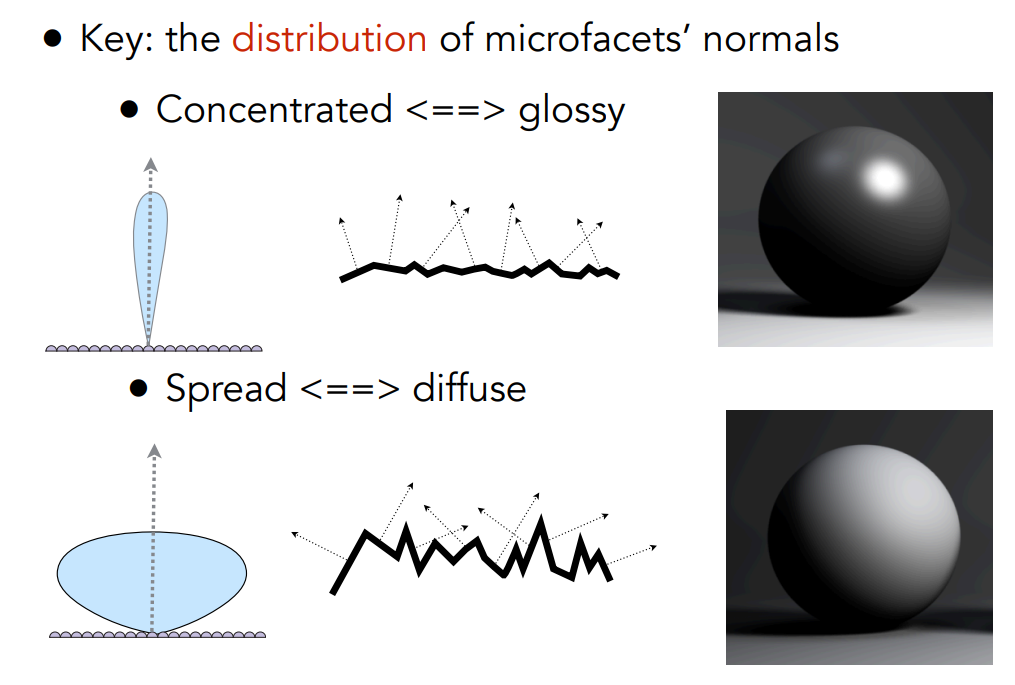
有不同的模型来描述法线分布,比如之前提到过的 Beckmann 法线分布函数:
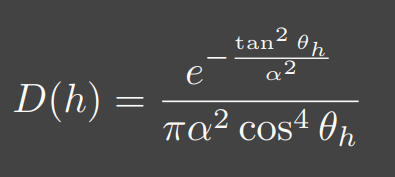
该函数由表面粗糙程度 $\alpha$ 和微表面法线与宏观法线(一般是 [0, 0, 1])的夹角 $\theta_h$ 来定义,从公式可以看出,Beckmann 法线分布实际上和高斯分布非常像,其中表面粗糙程度 $\alpha$ 就类似于正态分布的标准差,粗糙程度越大,法线分布就越分散,而这个正态分布是对于 $tan\theta_h$ 的正态分布, $tan\theta_h$ 的几何意义如下图:
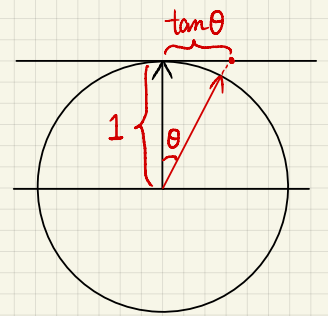
如果直接定义为夹角 $\theta_h$ 的正态分布,那么法线可能取到下半球,夹角就大于 90 度,而对于法线来说只有上半球有意义,因此定义为 $tan\theta_h$ 的正态分布的好处在于可以把上半球的所有法线方向对应到一个平面上的区间,这个区间是无穷大的,刚好是正态分布的积分区间,这样定义自然当法线在下半球的时候没有意义,是一个很巧妙的处理。
另一个更好的法线分布函数是 GGX 模型,也叫做 Trowbridge-Reitz(TR)模型,相较于 Beckmann 模型,GGX 是长尾(long tail)分布的:
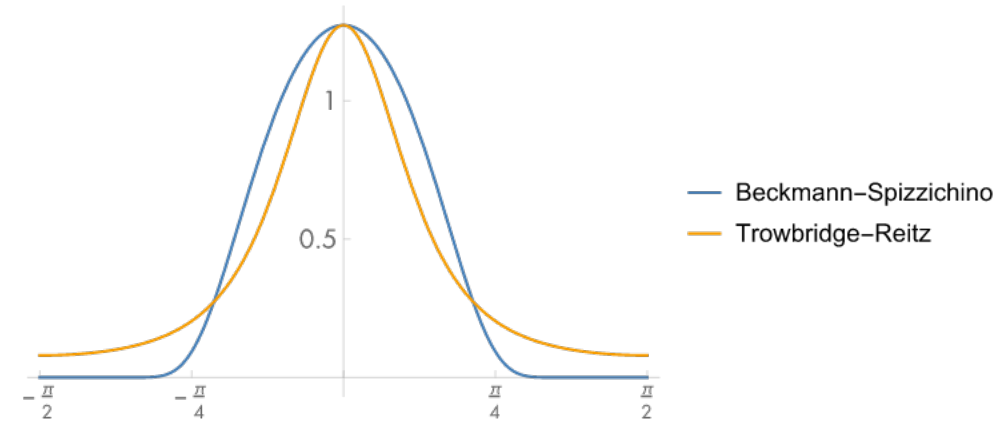
也就是过度更加平滑,在值较小的部分衰减速度也更小,这样的好处是高光区域和非高光区域的过渡会更加平滑,呈现出一种 Glossy 的效果,更加真实:

在 TR 模型的基础上还有一个更加通用的 GTR 法线分布,引入了一个可调的参数来控制长尾分布的程度:
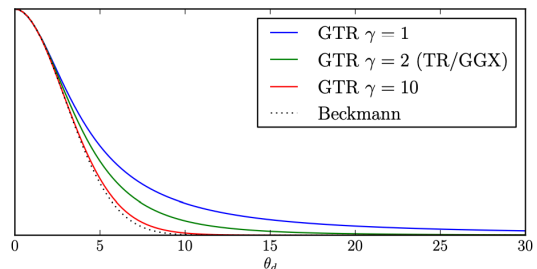
总之,法线分布函数描述的是微表面的法线方向分布,对于给定的入射和出射方向,可以得到半程向量,法线分布函数可以给出这个材质的表面上有多少微表面的法线是在这个半程向量方向上的,那么这些微表面才可以被看到。更准确的说,NDF 描述的是法线方向的概率分布,渲染时,对于每一个着色点都有不同的半程向量,这个半程向量对应的可以被看到的概率可以通过 NDF 得出,可以被看到也就是表面法线和半程向量方向一致,因此 NDF 给出的概率实际上是当前着色点的法线刚好和当前半程向量重合的概率,而一个点的着色结果是许多不同的半程向量的结果的加权平均,权值就是这个概率,这样就能得到这个着色点正确期望的着色结果。
1.3 几何项
几何项描述的是微表面之间的自遮挡现象,自遮挡现象有两种情况:

一种是入射光被其他微表面遮挡入射不进来,一种是反射光被其他微表面遮挡反射不出去,前者称为 shadowing,后者称为 masking,因此几何项也被称为 Shadowing-Masking Term。
从上面的定义可以看出,当我们垂直于表面观察时,几乎不会发生自遮挡,当我们观察方向越接近法线的垂直方向,自遮挡就会越严重,因此对应于上面的法线分布得出的几何项分布大概长这样:
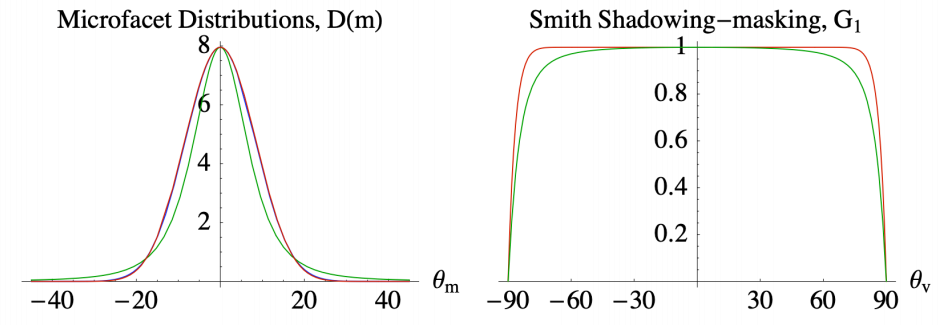
几何项的意义在于,当我们垂直于表面观察的时候,几何项就是 1,对最终结果不会有任何影响,但是当我们接近垂直于法线的方向观察时,比如一个球体的边缘:
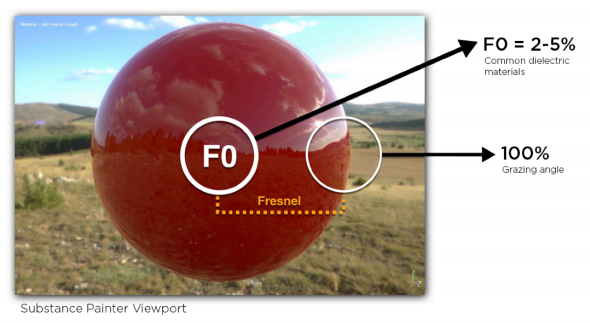
如果不考虑几何项,那么按照微表面 BRDF 的定义:
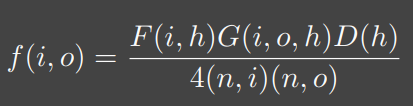
其他两项可以计算出正常结果,但是分母中有观察方向和法线的点乘,由于我们是接近垂直于法线的方向观察的,那么这个点乘结果就会接近于 0,于是整个BRDF 结果就会非常大,如果没有几何项来修正这个结果,那么最终的渲染图像上球体边缘就会是一圈白色。根据上面的几何项曲线可以看出,几何项在夹角接近 90 度的时候迅速变为 0,从而修正了这个非常大的结果。
2 Kulla-Conty Approximation
上面回顾了微表面模型,并进一步深入理解了各个项的作用,通过上面的分析我们可以很容易得出一个结论:微表面模型只考虑了光线在微表面之间的一次反射。被挡住的光线就认为看不到,这样做的结果就是微表面模型是能量不守恒的,如下图:

随着粗糙程度增大,最终的渲染结果会越来越暗,因为粗糙程度越大意味着法线分布越分散,从而微表面之间的遮挡也会越严重,在微表面模型中被遮挡掉的能量就被丢掉不考虑了,所以自然会越来越暗。
实际上被遮挡的光线还会在微表面之间弹射从而被看到,因此为了解决这个问题,提出了 Kulla-Conty 估计,用来近似估计光线在微表面之间的多次弹射。
Kulla-Conty 估计基于一个关键思想:微表面 BRDF 只考虑了没有被遮挡的能量,那么如果能再设计一个 BRDF 来专门描述被遮挡的能量就可以修正微表面的结果了。
于是首先要知道没有被遮挡的能量是多少,我们假设入射光强度恒为 1,然后对微表面 BRDF 的渲染方程在整个半球面上积分:
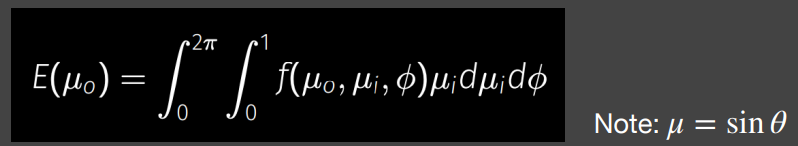
注意上面的式子中用了一个简单的积分换元,把 $d\theta$ 换成了 $dsin\theta$,这样一来原本渲染方程中的 cos 项也就没有了,光照项为常数 1,因此上面的积分结果就代表了微表面模型中在出射方向 $\mu_o$ 上全部被看到的能量总和,因为光照项为 1,所以该结果是一个系数,表示出射方向 $\mu_o$ 上被看到的能量占全部能量的比例。
于是因为遮挡而没被看到的能量总和自然就是 $1-E(\mu_o)$,因此,我们要设计一个 BRDF 来专门描述被遮挡的能量,那么这个 BRDF 在半球面上的积分结果就必须是 $1-E(\mu_o)$。
考虑到 BRDF 具有双向可逆性,因此 Kulla-Conty 估计设计了这样一个 BRDF:
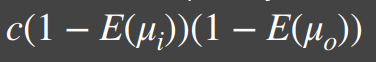
这个 BRDF 的形式并不是唯一的,只要能保证函数在半球的积分结果是 $1-E(\mu_o)$ 就可以,只是 Kulla-Conty 这样设计既把积分结果本身放到了函数中,还考虑了双向可逆的性质,非常巧妙。
于是通过积分结果为 $1-E(\mu_o)$ 可以求出常数 c:
$$
c = \frac{1}{\pi(1-E_{avg})}
$$
其中:
$$
E_{avg} = \frac{\int_0^1E(\mu)\mu d\mu}{\int_0^1\mu d\mu} = 2\int_0^1E(\mu)\mu d\mu
$$
相当于对上面的 $E(\mu_o)$ 做了一个加权平均,权值就是各个方向的夹角正弦 $\mu$,于是整个 Kulla-Conty 估计就是:
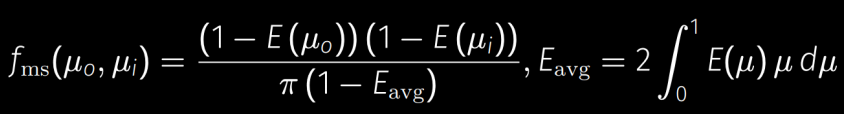
容易验证该函数在半球面上积分结果为 $1-E(\mu_o)$:
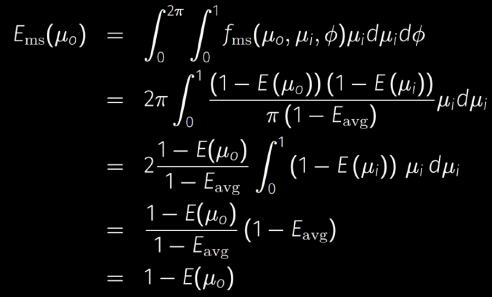
因此这个函数可以作为描述被遮挡的能量的 BRDF,现在的问题是 $E_{avg}$ 是对一个积分 $E(\mu)$ 再进行积分,实时计算起来比较复杂,所以需要进行预计算。
对于 $E(\mu)$ 这个积分,是对全部入射方向 $\mu_i$ 的积分,因此积分结果只与观察方向和法线的夹角正弦 $\mu_o$ 和粗糙程度 $\alpha$ 有关,于是预计算的积分结果可以用一张二维纹理来存储:
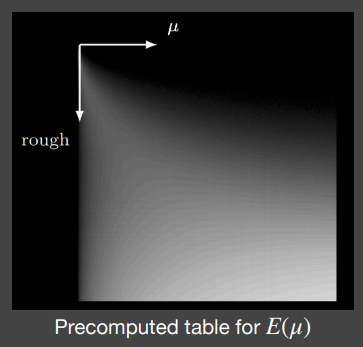
而对于 $E_{avg}$ 这个积分,是对 $\mu_o$ 的积分,所以积分结果只与粗糙程度 $\alpha$ 有关,只需要一个一维纹理就可以存储。
将 Kulla-Conty 的结果加到微表面 BRDF 的结果上就可以近似模拟光线在微表面之间多次弹射的结果,达到能量守恒:

接下来还有最后一个问题,上面的所有推导都是假设物体表面没有颜色,也就是反射率恒为 1,如果物体表面有颜色,那么能量在每次弹射后都会损失,如何计算这种损失来得到正确的结果呢?
Kulla-Conty 又计算了菲涅尔项的加权平均:
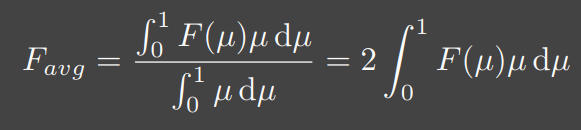
这表示每次弹射,表面上有多少能量被反射。这类似于上面的 $E_{avg}$, $E_{avg}$ 表示表面上有多少能量没被遮挡能够被看到,于是我们可以直接看到的能量就可以表示为:
$$
F_{avg}E_{avg}
$$
没被看到的能量就是:
$$
F_{avg}(1-E_{avg})
$$
这部分能量会在微表面之间继续弹射,于是经过一次弹射后被我们看到的能量就是:
$$
F_{avg}(1-E_{avg})·F_{avg}E_{avg}
$$
以此类推,可以写出经过无数次弹射后的能量,将这些能量加起来,就可以得到当物体有颜色的时候,光线在微表面之间多次弹射后反射出的能量,这是一个级数求和问题,最终的结果是:
$$
\frac{F_{avg}E_{avg}}{1-F_{avg}(1-E_{avg})}
$$
将这个系数乘到 Kulla-Conty 的 BRDF 上就可以得到有颜色的情况下被遮挡的能量的 BRDF 了。

3 Linearly Transformed Cosines(LTC)
有了微表面 BRDF,另一个需要解决的问题是如何使用微表面模型进行渲染。线性变换余弦(LTC)方法是用来解决多边形面光源下,使用微表面 BRDF,主要是 GGX 法线模型的渲染而提出的方法(不考虑阴影)。
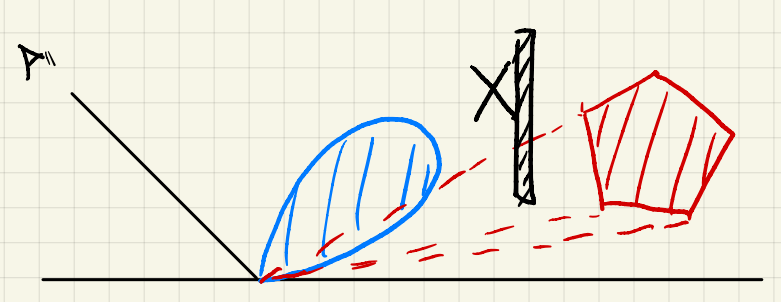
当然 LTC 不仅适用于上述情况,对于类似 GGX 法线分布的其他微表面模型也都有很好的效果。
在离线渲染中处理这样的渲染自然是对面光源进行采样计算,但实时渲染需要快速得到渲染结果,而不同的 BRDF 我们不知道它的分布是什么样的,所以也不容易快速求出这个 BRDF 积分的渲染方程的解析解,因此 LTC 将 BRDF 变换成一个 cos 函数,然后对所有的方向、以及面光源(积分区域)都做同样的变换:
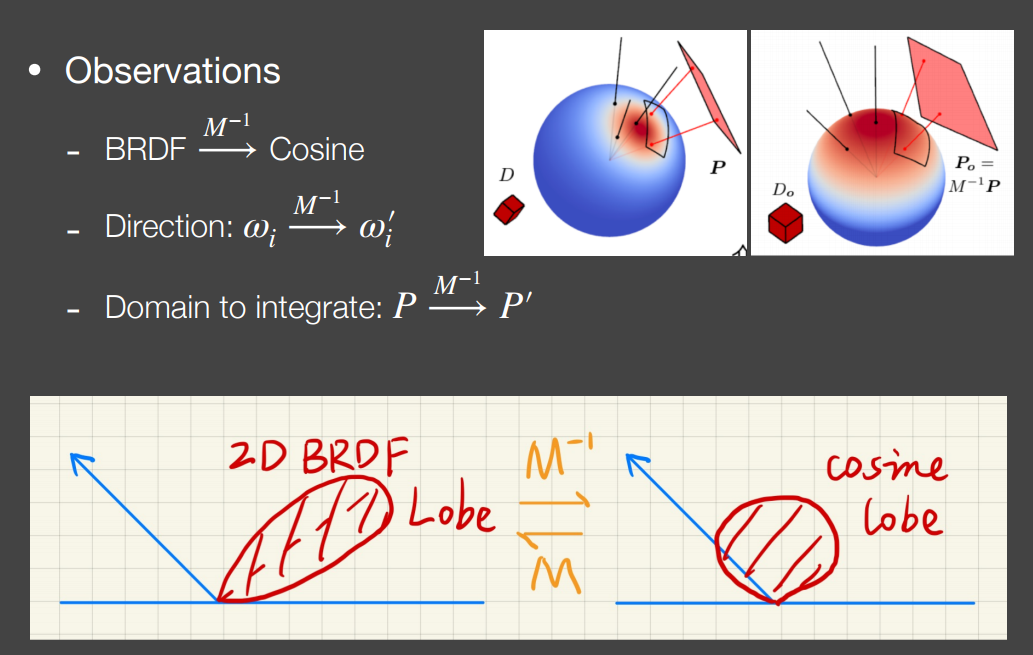
这样就将原积分转化为了一个对余弦函数的积分,保证可以快速求出解析解。具体来说,就是将原本的函数 $F(w_i)$ 变换为 $cos(w_i)$,为了便于理解,我们假设 BRDF 是各向同性的,于是 $F(w_i)$ 实际上和方位角无关,在出射方向固定的情况下就是一个只与俯仰角有关的一维函数,所以可以变换到一维的 cos 函数上,事实上 LTC 也可以处理各向异性的情况,这里就不展开讨论了。
然后将积分变量 $dw_i$ 同样变换为 $dw’_{i}$,实际上就是对原积分进行了换元:
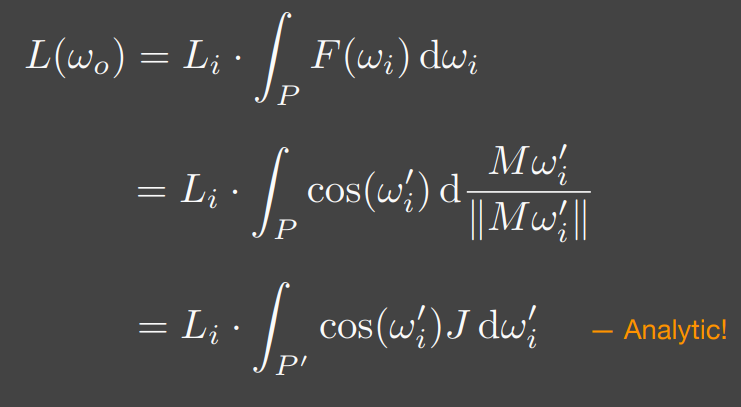
这样就可以快速求出解析解了。LTC 方法虽然思路很简单,但是效果却非常优秀,因此目前被广泛使用:

4 Disney’s Principled BRDF
Disney’s Principled BRDF 是目前工业界非常知名的,非常强大的开源 BRDF。微表面 BRDF 的问题之一在于不能够表达复合材质,现实世界中许多材质不是单一的,是多种材质的组合,比如蒙上一层塑料布的木头桌子,那么它的表面就有多层材质,光照表现自然和普通桌子不同,而 Disney’s Principled BRDF 具有强大的表达能力,可以表达各种复合材质。
并且 Disney’s Principled BRDF 摒弃了传统基于物理的材质的各种物理参数,只使用一些非常符合人直觉的参数就可以进行调节,对于艺术家非常友好,这也是迪士尼设计这个 BRDF 的原则之一,这些原则有:
- 使用符合人直觉的参数而不是各种难懂的物理量
- 越少的参数越好
- 所有参数都是从 0 到 1 调节的
- 在一些合理的情况下允许参数不在 0 到 1 范围内
- 所有参数的任意组合都必须得出合理的结果,而不是某些非常奇怪的结果
能够满足上述原则的 BRDF 可以说是完美的,虽然严格来说迪士尼的 BRDF 不是基于物理的,而是进行了各种非常复杂的拟合,但是也常被归为基于物理的 BRDF。
下图是一些可以调节的参数和得出的材质效果:
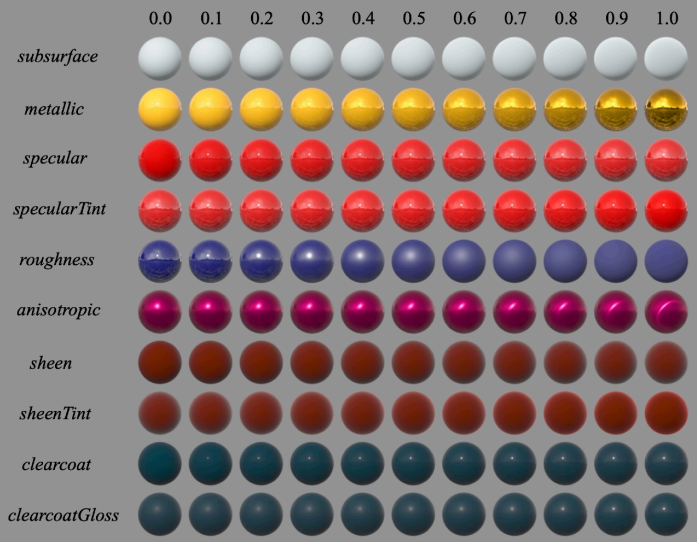
从上到下依次是:
- 次表面散射 subsurface:值越大次表面散射越严重,物体看起来更像一个平面
- 金属度 metallic:值越大物体越像金属
- 高光度 specular:值越大物体高光反射越强
- 高光颜色 specularTint:可以调节高光反射的颜色
- 粗糙程度 roughness:值越大物体表面越粗糙
- 各向异性程度 anisotropic:值越大物体表面越呈现各向异性
- 绒毛 sheen:绒毛相当于物体表面每个点都有一根朝向法线方向的绒毛,表现出来就是物体边缘会有模糊感,值越大绒毛越明显
- 绒毛颜色 sheenTint:控制绒毛颜色
- 表面通透 clearcoat:类似于给物体表面蒙上一层透明的漆,值越大这个效果越明显
- 表面通透颜色 clearcoatGloss:表面通透高光的锐利度,值越大高光越锐利
上面的所有参数可以随意组合,表达各种复合材质,所以迪士尼 BRDF 的表达能力非常强。
5 Specular Glossiness 模型
Specular Glossiness(SG)模型是在 Disney’s Principled BRDF 的启发下提出的便于实时渲染的 PBR 材质模型,SG 将所有描述材质需要用到的值都存在各种纹理中,渲染时只需要通过简单的纹理采样就可以计算出基于物理的光照结果,不需要调整任何参数,非常方便。
SG 模型使用三张纹理来存储信息,分别是:Diffuse、Specular 和 Glossiness。

Diffuse 存储物体的基础颜色,使用 RGB 三个通道;Specular 存储菲涅尔项的基础反射率,也就是菲涅尔近似公式中的 F0,同样对应 RGB 三个通道;Glossiness 是一个标量,用于控制表面光滑程度。
通过这三张纹理,就可以得到物体表面任何一个点对应的 F、D 和 G 项,从而根据微表面模型计算光照结果,下面是使用 SG 模型计算着色的代码,可以非常直观的感受到 SG 模型有多方便:

首先根据漫反射颜色计算出了漫反射项,然后根据微表面模型计算高光反射项,其中粗糙程度根据 Glossiness 采样结果得到,基础反射率 F0 根据 Specular 采样结果得到,再结合各种简单的点乘就可以得到 D、F 和 G 项,最后根据公式计算微表面 specular 结果,加上漫反射结果就是整个 BRDF 结果。有了 BRDF 就可以根据渲染方程得到着色结果了。
6 Metallic Roughness 模型
Metallic Roughness(MR)是对 SG 模型的又一层封装,SG 模型可以自由地调节漫反射颜色和基础反射率,但有时这对于艺术家来说还是不够直观,因此 MR 使用了另外三个贴图来描述材质:Base Color、Roughness 和 Metallic。
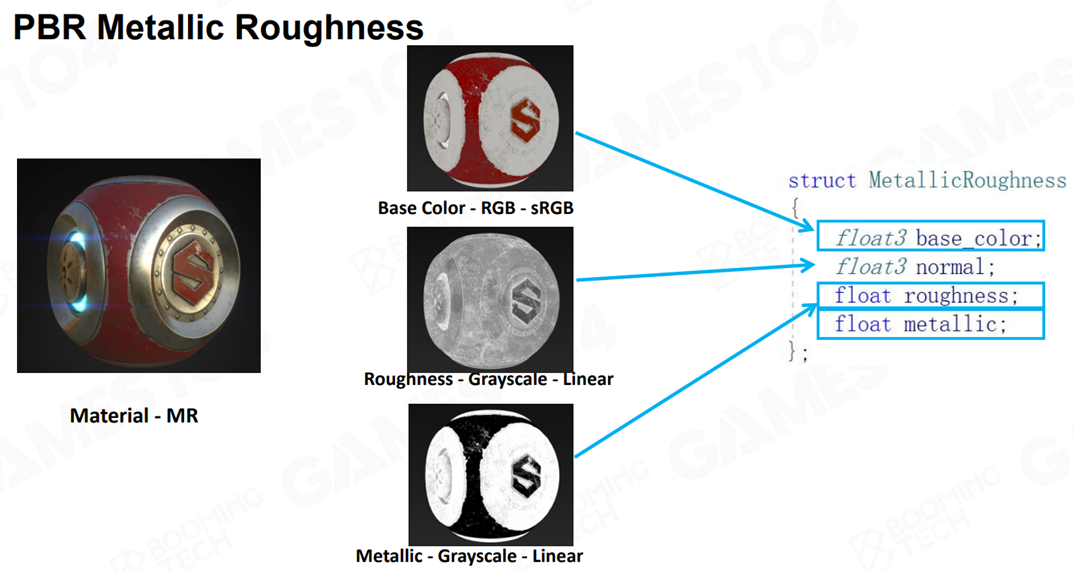
其中 Base Color 是物体的基础颜色,RGB 三通道;Roughness 和 Metallic 都是标量,分别代表表面粗糙程度和金属度。使用的时候游戏引擎内部会将这些值转化为 SG 模型中的值,下面是转化代码:

可以看到金属度 Metallic 是一个插值系数,用来从 base color 中取出一定的颜色到介质基本的颜色上,从而构成 SG 模型中的 F0,回顾前文中菲涅尔项的曲线图,金属的基础反射率是非常高的,所以金属度高的时候 base color 中很大一部分颜色就被取出到 F0 中,使得基础反射率变高,而 base color 剩下的颜色就作为 SG 中的 diffuse,于是金属度高就会使 diffuse 很小,也就是金属几乎不会发生漫反射,这和菲涅尔项描述的是完全一致的,所以 MR 模型中的基础颜色就是 diffuse 和 specular 的结合,金属度 Metallic 可以将他们拆分开来,但 base color 的概念对于艺术家来说要比 diffuse 和 specular 更好理解。粗糙程度 Roughness 和 SG 中的光滑程度 Glossiness 相反,二者之间可以互相转化,本质上是一样的。
MR 和 SG 相比,更便于人们理解,但没有 SG 灵活,因为 MR 不能够自己调节 F0,而是全部包含在了 base color 中,但也因此避免了艺术家如果使用 SG,但给出了错误的 F0 而导致的菲涅尔项错误的情况,各有利弊。