在之前的光栅化渲染器中,我们在光栅化插值的过程中对所有顶点的属性都除以了该顶点的深度值 w,然后又在线性插值之后乘以了该点的深度值,这样才能得到正确的插值属性,这一步叫做透视插值校正。这一节我们来详细讨论透视插值校正的具体原理。
1 为什么需要透视插值校正
透视投影我们已经非常熟悉了,透视投影是为了模拟人眼所看到的近大远小的效果,比如一个正方形,如下图:
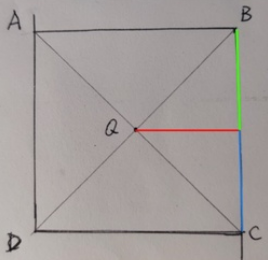
如果是正交投影,那么点 Q 就在 BC 连线中点处,而如果是透视投影,如下图:
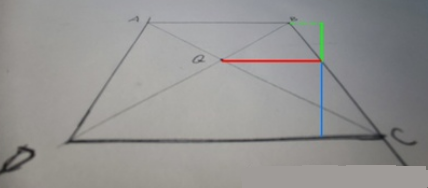
点 Q 就不再处于 BC 连线的中间处了,在我们的渲染器中纹理出现变形的原因就是我们在对顶点的纹理坐标进行插值的时候没有考虑透视的影响。如下图,红色坐标为纹理坐标,黑色为顶点位置:
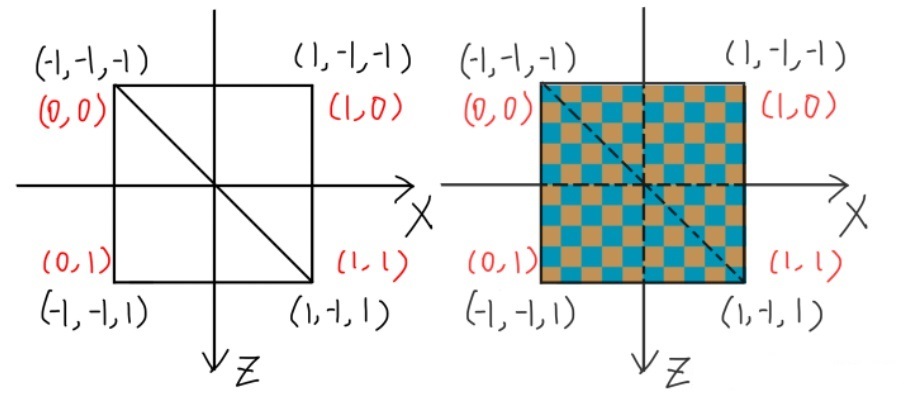
当摄像机视线垂直于平面时,将贴图按照 uv 坐标插值,贴到正方形上会如右图所示,不会出现任何问题,但如果相机不垂直于平面:
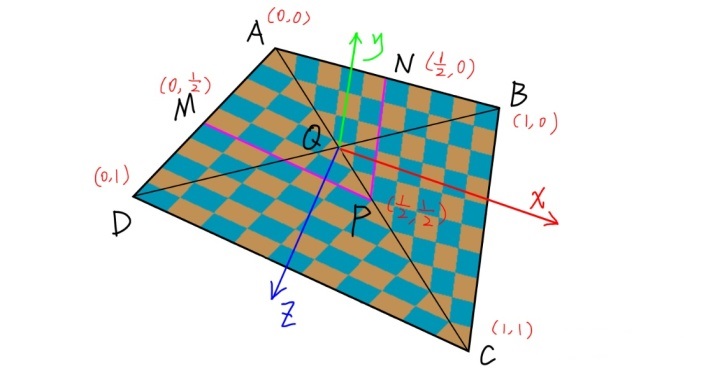
本来按照正确的透视,正方形的中心点应该在 AC 和 BD 的交点 Q,我们应该把纹理坐标为 (0.5, 0.5) 的颜色值赋给 Q,但是图中却赋给了 P 点,这是因为我们在光栅化插值的时候,使用的是屏幕坐标进行的线性插值,屏幕坐标是投影后的坐标,是没有考虑近大远小的。
也就是说通,过屏幕坐标插值,可以得到 AC 的中点为点 P,AB 的中点为点 N,AD 的中点为点 M,这些都是投影后屏幕上线段的中点,而不是实际这个正方形在空间中线段的中点,因此就会出现纹理映射错误的情况。所以这时候我们就需要进行透视插值校正。
2 如何进行透视插值校正
我们在二维空间中进行推导会简单许多。下图为二维空间中的投影,因为是二维,所以我们把 x 坐标全部置 0,各种几何关系如图所示:
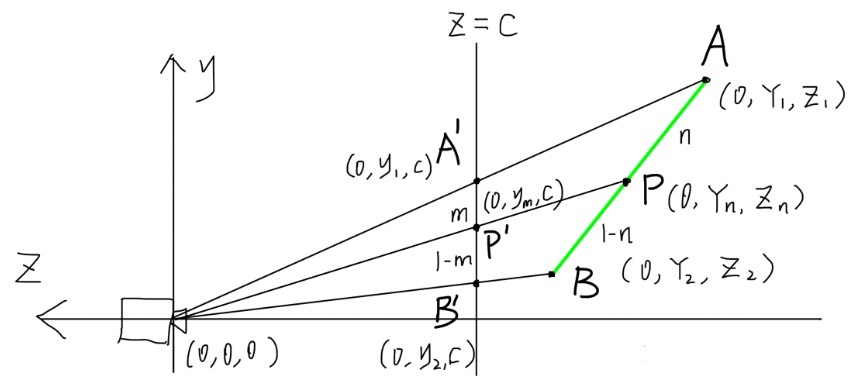
二维空间中的线段 AB 被投影到 Z = C 平面上,显示为线段 A’B’,利用投影平面的坐标进行插值可以得到:
$$
P’ = (1-m)A’ + mB’
$$
于是现在的问题是,如何通过屏幕上的点 P‘ 得到空间中原本的点 P,并求出一个插值关系:
$$
P = (1-n)A + nB
$$
最简单的方法自然是对点 P’ 应用透视投影变换的逆变换,但矩阵变换太麻烦,我们完全可以通过几何关系解决这个问题。
在图中添加两条辅助线:
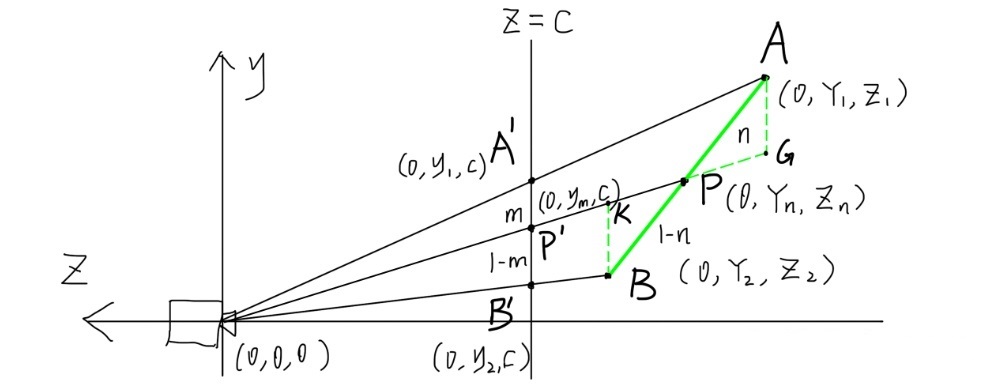
根据三角形相似可以得到:
$$
\frac{n}{1-n} = \frac{|AG|}{|BK|} = \frac{|A’P’|\frac{Z_1}{c}}{|B’P’|\frac{Z_2}{c}} = \frac{mZ_1}{(1-m)Z_2}
$$
等式两边取倒数可得:
$$
\frac{1}{n} - 1 = \frac{(1-m)Z_2}{mZ_1}
$$
由此可以解得:
$$
n = \frac{mZ_1}{mZ_1 + (1-m)Z_2}
$$
这样我们就得到了已知屏幕空间的插值系数 m,求观察空间的插值系数 n 的方法。使用插值系数 n 就可以对顶点的任意属性进行插值了。比如点 P 的 Z 坐标:
$$
Z_n = (1-n)Z_1 + nZ_2 = \frac{(1-m)Z_2}{mZ_1 + (1-m)Z_2}Z_1 + \frac{mZ_1}{mZ_1 + (1-m)Z_2}Z_2
$$
化简后得到:
$$
Z_n = \frac{Z_1Z_2}{mZ_1 + (1-m)Z_2} = \frac{1}{\frac{1-m}{Z_1} + \frac{m}{Z_2}}
$$
这样计算其他属性的插值就可以直接将 $Z_n$ 带入,为什么要将 $Z_n$ 带入呢?因为我们的观察方向都是沿着 -Z 轴方向,所以透视的缩放关系只和深度 Z 有关。比如求点 P 的纹理坐标:
$$
UV_P = \frac{(1-m)Z_2}{mZ_1 + (1-m)Z_2}UV_A + \frac{mZ_1}{mZ_1 + (1-m)Z_2}UV_B
$$
将 $Z_n$ 带入得:
$$
UV_P = Z_n(\frac{1-m}{Z_1}UV_A + \frac{m}{Z_2}UV_B)
$$
上式就是我们在代码中实现的,将所有顶点的所有属性都除以其深度值 w(经过投影变换,w 是 -Z,一次乘法一次除法负号消掉了),然后使用屏幕坐标对顶点进行所有属性的线性插值之后再乘以插值点的深度值,就完成了线性插值的透视校正。
现在推广到三维空间,可以得到:
$$
Z_n = \frac{1}{\frac{1-u-v}{Z_1} + \frac{u}{Z_2} + \frac{v}{Z_3}}
$$
其中 u 和 v 是重心插值系数:
$$
P = (1-u-v)A + uB + vC
$$
于是在三维空间中,点 P 的纹理坐标为:
$$
UV_P = Z_n(\frac{1-u-v}{Z_1}UV_A + \frac{u}{Z_2}UV_B + \frac{v}{Z_3}UV_C)
$$
于是同样的,在透视除法中,将所有顶点的所有属性都除以其深度值 w(经过投影变换,w 是 -Z,一次乘法一次除法负号消掉了),然后使用屏幕坐标对顶点进行所有属性的重心插值之后再乘以插值点的深度值,就完成了重心插值的透视校正。