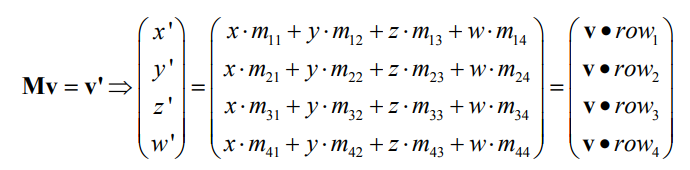【光栅化渲染器】（六）剔除与裁剪

目前我们已经基本实现了一个最简单的渲染管线，不过还有很多功能没有加入，这一节开始来完善我们的渲染管线。首先在之前的实现中，正方体大多数情况下都只有 3 个面正对我们，其他三个面是看不见的，也就完全不需要渲染，为了之后应对更复杂的模型和场景，提高渲染效率，我们需要先实现剔除和裁剪算法。

1 剔除和裁剪概览

在整个渲染管线中，需要进行多次剔除与裁剪，分别是：视锥剔除、正面/背面剔除、齐次裁剪。

• 视锥剔除一般发生在 CPU 阶段，通过 AABB、OBB 等将物体包围起来，然后与视锥体做碰撞检测，可以直接剔除掉完全不可见的物体，运算量较低但精度也较低。
• 正面/背面剔除在顶点着色器之后，齐次裁剪之前进行，将不需要渲染的图元直接剔除掉；一般来说这一步也可以在齐次裁剪之后进行，因为操作比较简单，所以可以在世界空间运算也可以在 NDC 中运算，取决于管线的设计。
• 齐次裁剪自然是在裁剪空间中进行，即顶点着色器之后，透视除法之前。在透视除法之前是因为如果有物体在摄像机的位置，会出现 w = 0 ，做透视除法的时候会出现除零错误。这一阶段是将在视口外的图元丢弃，一部分在视口内的图元，会进行裁剪，生成新的多边形。当然做裁剪的性能消耗也不小，很多情况下裁剪之后并不比直接把原来的多边形画出来丢弃一部分更快，尤其是 GPU 并不适合做这种判断条件比较多的工作。现代 GPU 通常是用一个比视口大很多（10倍以上？）的虚拟视口来裁剪，那种超出一点点的，就直接画了吧，GPU 性能没那么捉襟见肘。

2 视锥剔除

视锥剔除首先要计算物体的包围盒，一般来说如果场景管理使用 BVH 的话，层次包围盒已经计算好了，直接遍历整个 BVH 树即可。然后获得视锥体的六个面的方程，用包围盒和六个面进行碰撞检测，具体实现可以有很多种方法，这里我们实现世界空间下的视锥剔除，流程如下：

• 计算包围要绘制物体的 AABB（世界空间），实际我们逐图元计算，剔除掉完全在视锥体外的图元，这样一来就和后面的齐次裁剪中的剔除所做的工作几乎一样了，但这里只是为了学习原理，实际的渲染管线中是利用 BVH 等来剔除掉完全不在视锥体内的物体，而图元是在齐次裁剪的时候剔除的
• 获得视锥体六个面的平面方程（世界空间）
• 判断 AABB 的顶点在六个面的内侧还是外侧，也可以判断最小点和最大点，实现方法不唯一
• 剔除掉所有顶点完全在某一面外侧的物体，我们这里是图元

2.1 获取视锥平面方程

那么如何获取视锥体六个平面的方程呢？通过 MVP 变换矩阵就可以直接得出，并且使用 MVP 三个矩阵的不同组合可以得出不同空间下的视锥体平面方程。具体推导的原文可以查看：Fast Extraction of Viewing Frustum Planes from the WorldView-Projection Matrix

我们首先定义一个顶点 $v = (x, y, z, w=1)$，以及一个 4 * 4 的矩阵 $$M = m_{ij}$$，这个矩阵可以是投影矩阵 P，也可以是 VP，还可以是 MVP，总之经过矩阵 $M$ 后，顶点 $v$ 就被转换到了一个规范立方体中变为 $v’ = (x’, y’, z’, w’)$，这个过程可以写为：

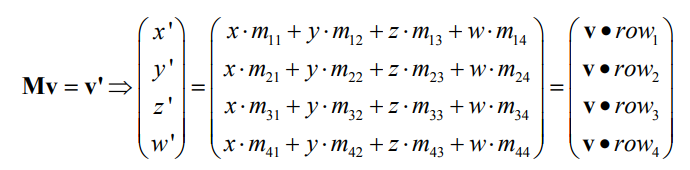
规范立方体的范围是 [-w’, w’]，因此如果这个顶点在立方体内，那么必须满足：

• -w’ < x’ < w’
• -w’ < y’ < w’
• -w’ < z’ < w’

这实际上描述了顶点和视锥体六个平面的关系，原文中以下表列出：

现在以顶点和左侧平面的关系为例，只需要判断 -w’ < x’ 就可以了，根据矩阵乘法，可以得出：
$$
-w’ < x’ \Rightarrow -(row4 · v) < (row1 · v)
$$
于是可以进一步得到：
$$
(row1 + row4) · v > 0
$$
将矩阵元素带入展开可以写成：
$$
(m_{11}+m_{41})*x + (m_{12}+m_{42})*y + (m_{13}+m_{43})*z + (m_{14}+m_{44})*w > 0
$$
由于 $w = 1$，因此可以写为：
$$
(m_{11}+m_{41})*x + (m_{12}+m_{42})*y + (m_{13}+m_{43})*z + (m_{14}+m_{44}) > 0
$$
这实际上已经得到了视锥体左平面的方程，因为空间中一个平面可以表示为 $$Ax + By + Cz + D = 0$$，所以视锥体左平面的方程中：
$$
A = m_{11}+m_{41},\ B = m_{12}+m_{42},\ C = m_{13}+m_{43},\ D = m_{14}+m_{44}
$$
类似的可以得出其他几个面的方程：

上面说过， 4 * 4 的矩阵 $$M$$ 可以是投影矩阵 P，也可以是 VP，还可以是 MVP，不同的组合得到的视锥体平面方程是不同空间下的：

• 当矩阵是 P 时，得到的是观察空间下的平面
• 当矩阵是 VP 时，得到的是世界空间下的平面
• 当矩阵是 MVP 时，得到的是模型空间下的平面

2.2 判断顶点与平面的关系

顶点与平面的关系判断非常简单，类似于二维中点和直线的关系，将顶点坐标 $(x, y, z)$ 带入平面方程计算得到点到平面的距离 $$d = Ax + By + Cz + D$$：

• d > 0 时，点在平面法向所指的区域
• d < 0 时，点在平面法向反方向所指的区域
• d = 0 时，点在平面上

2.3 实现

我们使用世界空间下的视锥体剔除，首先在 math.h 中加入视锥体六个平面的方程以及点和平面的关系判断函数：

// 视锥体的六个平面方程（世界空间下，传入的是 VP 矩阵），用于视锥剔除
// 所得的平面法向都是指向视锥体内部的
void ViewingFrustumPlanes(std::vector<glm::vec4>& result, const glm::mat4& vp) {
    //左侧  
    result[0].x = vp[0][3] + vp[0][0];
    result[0].y = vp[1][3] + vp[1][0];
    result[0].z = vp[2][3] + vp[2][0];
    result[0].w = vp[3][3] + vp[3][0];
    //右侧
    result[1].x = vp[0][3] - vp[0][0];
    result[1].y = vp[1][3] - vp[1][0];
    result[1].z = vp[2][3] - vp[2][0];
    result[1].w = vp[3][3] - vp[3][0];
    //上侧
    result[2].x = vp[0][3] - vp[0][1];
    result[2].y = vp[1][3] - vp[1][1];
    result[2].z = vp[2][3] - vp[2][1];
    result[2].w = vp[3][3] - vp[3][1];
    //下侧
    result[3].x = vp[0][3] + vp[0][1];
    result[3].y = vp[1][3] + vp[1][1];
    result[3].z = vp[2][3] + vp[2][1];
    result[3].w = vp[3][3] + vp[3][1];
    //Near
    result[4].x = vp[0][3] + vp[0][2];
    result[4].y = vp[1][3] + vp[1][2];
    result[4].z = vp[2][3] + vp[2][2];
    result[4].w = vp[3][3] + vp[3][2];
    //Far
    result[5].x = vp[0][3] - vp[0][2];
    result[5].y = vp[1][3] - vp[1][2];
    result[5].z = vp[2][3] - vp[2][2];
    result[5].w = vp[3][3] - vp[3][2];
}

//点到平面距离 d =  Ax + By + Cz + D;
// d < 0 点在平面法向反方向所指的区域
// d > 0 点在平面法向所指的区域
// d = 0 在平面上
// d < 0 返回 false
bool Point2Plane(const glm::vec3& v, const glm::vec4& p) {

    float sb = p.x * v.x + p.y * v.y + p.z * v.z + p.w;
    return sb >= 0;
}

为了便于管理，我们新建一个 Cull.h 来管理各类剔除函数，目前只有视锥体剔除：

//世界空间的视锥剔除
bool WorldFrustumCull(const std::vector<glm::vec4> ViewPlanes, const glm::vec4& v1, const glm::vec4& v2, const glm::vec4& v3)
{
    // 如果三个顶点都在某一个平面外侧，则剔除掉
    if (!Point2Plane(v1, ViewPlanes[0]) && !Point2Plane(v2, ViewPlanes[0]) && !Point2Plane(v3, ViewPlanes[0])) {
        return false;
    }
    if (!Point2Plane(v1, ViewPlanes[1]) && !Point2Plane(v2, ViewPlanes[1]) && !Point2Plane(v3, ViewPlanes[1])) {
        return false;
    }
    if (!Point2Plane(v1, ViewPlanes[2]) && !Point2Plane(v2, ViewPlanes[2]) && !Point2Plane(v3, ViewPlanes[2])) {
        return false;
    }
    if (!Point2Plane(v1, ViewPlanes[3]) && !Point2Plane(v2, ViewPlanes[3]) && !Point2Plane(v3, ViewPlanes[3])) {
        return false;
    }
    if (!Point2Plane(v1, ViewPlanes[4]) && !Point2Plane(v2, ViewPlanes[4]) && !Point2Plane(v3, ViewPlanes[4])) {
        return false;
    }
    // 远平面只保留完全在内的图元，部分在内的直接丢掉
    if (!Point2Plane(v1, ViewPlanes[5]) || !Point2Plane(v2, ViewPlanes[5]) || !Point2Plane(v3, ViewPlanes[5])) {
        return false;
    }
    return true;
}

然后在渲染流程中加入视锥体剔除，一般来说应该在 CPU 阶段进行，但是我们为了方便将视锥体剔除放在顶点着色器之后，因为顶点着色器之后才知道世界空间下的坐标：

class Draw {
private:
    int Width;
    int Height;
    FrameBuffer* FrontBuffer;
    Shader* shader;
    glm::mat4 ViewPortMatrix;
    std::string TexturePath;
    // 视锥体剔除用到的视锥体平面
    std::vector<glm::vec4> ViewPlanes;
    
    // 剔除开关
    bool FrustumCull;
public:
    Draw(const int& w, const int& h) :
        Width(w), Height(h), FrontBuffer(nullptr), shader(nullptr), FrustumCull(true)
    {
        ViewPlanes.resize(6, glm::vec4(0));
    }
    Draw(const int& w, const int& h, const std::string tpath) :
        Width(w), Height(h), FrontBuffer(nullptr), shader(nullptr), TexturePath(tpath), FrustumCull(true)
    {
        ViewPlanes.resize(6, glm::vec4(0));
    }
    ~Draw() {
        if (FrontBuffer)
            delete FrontBuffer;
        if (shader)
            delete shader;
        FrontBuffer = nullptr;
        shader = nullptr;
    }

    ...

    void DisableFrustumCull()
    {
        FrustumCull = false;
    }

    void EnableFrustumCull()
    {
        FrustumCull = true;
    }
        
    // 获取视锥体六个平面
    void UpdateViewPlanes() {
        ViewingFrustumPlanes(ViewPlanes, ProjectMatrix * ViewMatrix);
    }

    // 画网格
    void DrawMesh(const Mesh& mesh) {
        if (mesh.EBO.empty()) {
            return;
        }
        for (int i = 0; i < mesh.EBO.size(); i += 3) {
            Vertex p1, p2, p3;
            p1 = mesh.VBO[mesh.EBO[i]];
            p2 = mesh.VBO[mesh.EBO[i + 1]];
            p3 = mesh.VBO[mesh.EBO[i + 2]];
            //顶点着色器变换到裁剪空间
            V2F v1, v2, v3;
            v1 = shader->VertexShader(p1);
            v2 = shader->VertexShader(p2);
            v3 = shader->VertexShader(p3);

            // 视锥体剔除
            UpdateViewPlanes();
            if (FrustumCull && !WorldFrustumCull(ViewPlanes, v1.worldPos / v1.w, v2.worldPos / v2.w, v3.worldPos / v3.w))
            {
                continue;
            }

            //做透视除法，变换到NDC
            PerspectiveDivision(v1);
            PerspectiveDivision(v2);
            PerspectiveDivision(v3);
            // 视口变换，变换到屏幕空间
            v1.windowPos = ViewPortMatrix * v1.windowPos;
            v2.windowPos = ViewPortMatrix * v2.windowPos;
            v3.windowPos = ViewPortMatrix * v3.windowPos;
            // 光栅化
            ScanLineTriangle(v1, v2, v3);
        }
    }
    
    ...
}

3 正面/背面剔除

经过视锥体剔除将所有完全不在视锥体内的图元剔除掉之后，剩下的图元要么完全在视锥体内，要么部分在视锥体内，对于部分在视锥体内的图元需要进行裁剪，但因为裁剪是计算量较大的操作，为了进一步减少无用的运算，在此之前还要根据需要将背面（有时也需要将正面的剔除）的图元剔除掉，这一步操作比较简单，我们在世界空间计算。根据观察方向和图元的法线方向的夹角来判断图元是正对我们还是背对我们，原理在之前的 RTR 总结中有介绍，这里不再赘述。

也可以先做齐次裁剪，透视除法之后在 NDC 中进行正面/背面剔除，但要注意 NDC 是左手系，观察方向恒定为 (0, 0, 1)。无论在哪里计算，原理都是一样的。

在 Cull.h 中加入正面/背面剔除函数：

// 正面/背面
enum Face {
    Back,
    Front
};

// 世界空间的面剔除，剔除正向面或者逆向面
bool WorldFaceCull(Face face, const glm::vec4& v1, const glm::vec4& v2, const glm::vec4& v3) {

    // 叉乘得到法向量
    glm::vec3 tmp1 = glm::vec3(v2.x - v1.x, v2.y - v1.y, v2.z - v1.z);
    glm::vec3 tmp2 = glm::vec3(v3.x - v1.x, v3.y - v1.y, v3.z - v1.z);
    glm::vec3 normal = glm::normalize(glm::cross(tmp1, tmp2));
    // 世界空间下的观察方向
    glm::vec3 view = camera->Front;
    // 也可以在NDC中剔除，这时观察方向恒定为(0, 0, 1)，但上面的叉乘顺序顺序要颠倒一下，因为NDC是左手系
    //glm::vec3 view = glm::vec3(0, 0, 1);
    if (face == Back)
        return glm::dot(normal, view) > 0;
    else
        return glm::dot(normal, view) < 0;
}

然后在渲染流程中加入正面/背面剔除：

...
    
// 剔除开关
bool FrustumCull;
bool FaceCull;
Face CullMode;

...
    
void DisableFaceCull()
{
    FaceCull = false;
}

void EnableFaceCull(Face f)
{
    FaceCull = true;
    CullMode = f;
}

...

void DrawMesh(const Mesh& mesh) {
    if (mesh.EBO.empty()) {
        return;
    }
    for (int i = 0; i < mesh.EBO.size(); i += 3) {
        Vertex p1, p2, p3;
        p1 = mesh.VBO[mesh.EBO[i]];
        p2 = mesh.VBO[mesh.EBO[i + 1]];
        p3 = mesh.VBO[mesh.EBO[i + 2]];

        // 顶点着色器变换到裁剪空间
        V2F v1, v2, v3;
        v1 = shader->VertexShader(p1);
        v2 = shader->VertexShader(p2);
        v3 = shader->VertexShader(p3);

        // 视锥体剔除
        UpdateViewPlanes();
        if (FrustumCull && !WorldSpaceCull(ViewPlanes, v1.worldPos / v1.w, v2.worldPos / v2.w, v3.worldPos / v3.w))
        {
            continue;
        }
        
        // 正面/背面剔除
        if (FaceCull && WorldFaceCull(CullMode, v1.worldPos, v2.worldPos, v3.worldPos))
        {
            continue;
        }

        // 做透视除法，变换到NDC
        PerspectiveDivision(v1);
        PerspectiveDivision(v2);
        PerspectiveDivision(v3);

        // 视口变换，变换到屏幕空间
        v1.windowPos = ViewPortMatrix * v1.windowPos;
        v2.windowPos = ViewPortMatrix * v2.windowPos;
        v3.windowPos = ViewPortMatrix * v3.windowPos;

        // 光栅化
        ScanLineTriangle(v1, v2, v3);
    }
}

然后修改主函数：

...
    
    // 初始化渲染器
    dw = new Draw(SCR_WIDTH, SCR_HEIGHT, TEXTURE_PATH);
    dw->Init();
    dw->ClearBuffer(glm::vec4(0, 0, 0, 1));
    // 开启视锥体剔除,实际上默认已经开启
    dw->EnableFrustumCull();
    // 开启背面剔除，背面剔除默认关闭，需要手动开启并指定剔除模式
    Face CullMode = Back;
    dw->EnableFaceCull(CullMode);

...

4 齐次裁剪

最后是比较麻烦的齐次裁剪，之前说过，渲染管线中进行齐次裁剪的位置是投影之后，透视除法之前，我们知道，在世界空间和观察空间中，一个点的坐标是 (X, Y, Z, 1)，经过透视投影之后变为 (X’, Y’, Z’, -Z)，再除以 W 坐标变化到 NDC 中 (X’/-Z, Y’/-Z, Z’/-Z, 1)。这其中，如果一个点在观察者的身后，其观察坐标 Z 会大于 0（观察空间是右手系），那么透视投影之后 W 会小于 0，进行透视除法会导致顶点的 X, Y 坐标上下左右翻转。如下图：

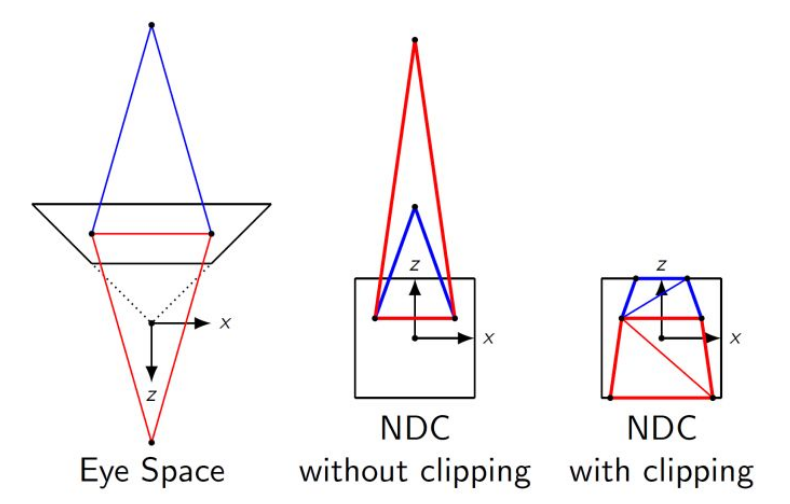
并且如果一个物体在相机平面上，会在透视除法时导致除零错误。

透视投影之后，透视除法之前的坐标空间被称为裁剪空间，也叫齐次（裁剪）空间，它实质上是一个四维空间，变换到齐次空间的顶点之间仍然是线性相关的（可以直接使用线性插值而不是透视插值）。这是因为透视除法将所有坐标除以 w 才会真正破坏顶点之间的线性关系，所以也有这种说法：真正的投影是通过透视除法完成的。

这时，在视锥体中的点一定满足如下条件：

• $-w < x,y,z < w$
• $near<w<far$

如果不满足这个条件的点，就需要被剔除，因此我们可以写出代码：

// 裁剪空间剔除
bool ClipSpaceCull(const glm::vec4& v1, const glm::vec4& v2, const glm::vec4& v3)
{
    // 三个点的w都在near或far之外则需要剔除
    if (v1.w <= camera->Near && v2.w <= camera->Near && v3.w <= camera->Near)
        return false;
    if (v1.w >= camera->Far && v2.w <= camera->Far && v3.w <= camera->Far)
        return false;
    // 任意一个点在规范立方体内则不需要剔除，等待进行下一步裁剪
    if (v1.x <= v1.w || v1.y <= v1.w || v1.z <= v1.w)
        return true;
    if (v2.x <= v2.w || v2.y <= v2.w || v2.z <= v2.w)
        return true;
    if (v3.x <= v3.w || v3.y <= v3.w || v3.z <= v3.w)
        return true;
    return false;
}

接下来是对没有被剔除的片元进行裁剪，使用 Sutherland-Hodgeman 裁剪算法，也叫做逐边裁剪算法，它的原理很简单，在二维中就是每次使用裁剪框的一条边去裁剪多边形的每一条边，生成新的顶点并作为下一条裁剪边的输入，如下图：

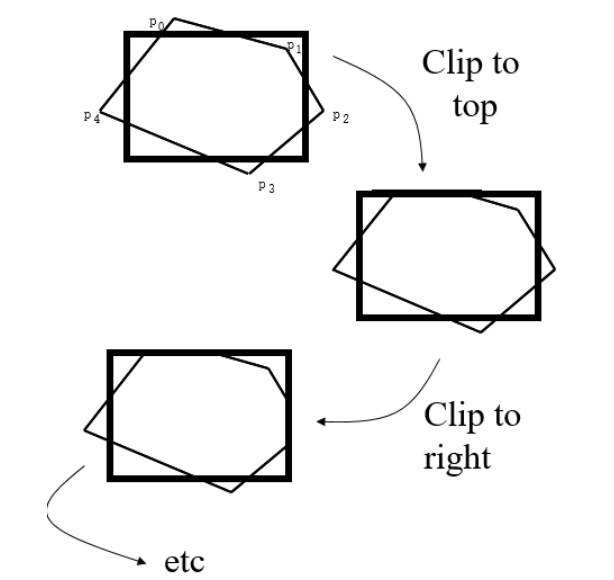
这个算法在齐次空间也同样适用（而且可以推广到任意维），与二维的区别是，裁剪平面变为了 6 个，而不是四条线了。

使用点到平面的距离来判断点在平面的内外，和之前的计算方法类似，之前的计算方法是：

bool Point2Plane(const glm::vec3& v, const glm::vec4& p) {

    float sb = p.x * v.x + p.y * v.y + p.z * v.z + p.w;
    return sb >= 0;
}

该函数只适用于世界空间或者观察空间等 w 为 1 的空间中，而我们现在是在裁剪空间，顶点的 w 值不为 1， 因此不能省略顶点的 w，所以需要重新写一个函数：

// 判断点是否在裁剪平面法线所指方向，即内部
bool Inside(const glm::vec4& line, const glm::vec4& p) {

    return line.x * p.x + line.y * p.y + line.z * p.z + line.w * p.w >= 0;
}

同时我们还需要一个函数直接判断三个顶点是否都在视口内，这样就无需裁剪了，也很简单：

// 判断是否所有顶点都在内部
bool AllVertexsInside(const std::vector<V2F> v) {
    for (int i = 0; i < v.size(); i++) {
        if (fabs(v[i].windowPos.x) > fabs(v[i].windowPos.w))
            return false;
        if (fabs(v[i].windowPos.y) > fabs(v[i].windowPos.w))
            return false;
        if (fabs(v[i].windowPos.z) > fabs(v[i].windowPos.w))
            return false;
    }
    return true;
}

接下来是计算两个点连线与平面的交点，这可以通过插值实现，分别在一个平面两侧的两个点 A 和 B，它们连线与平面的交点 C 可以通过权重 da / (da - db) 从 A 到 B 插值得到。其中 da 和 db 分别是点 A 和 B 到裁剪平面的距离，可以通过上面函数的方法计算得到：

//交点，通过端点插值得到
V2F Intersect(const V2F& v1, const V2F& v2, const glm::vec4& line) {
    float da = v1.windowPos.x * line.x + v1.windowPos.y * line.y + v1.windowPos.z * line.z + v1.windowPos.w * line.w;
    float db = v2.windowPos.x * line.x + v2.windowPos.y * line.y + v2.windowPos.z * line.z + v2.windowPos.w * line.w;

    float weight = da / (da - db);
    return V2F::lerp(v1, v2, weight);
}

最后是 Sutherland-Hodgeman 裁剪算法，代码很好理解：

// SutherlandHodgeman裁剪算法
// 输入三个顶点，输出裁剪后的顶点组
std::vector<V2F> SutherlandHodgeman(const V2F& v1, const V2F& v2, const V2F& v3) {
    std::vector<V2F> output = { v1,v2,v3 };
    if (AllVertexsInside(output)) {
        return output;
    }
    for (int i = 0; i < ViewLines.size(); ++i) {
        std::vector<V2F> input(output);
        output.clear();
        for (int j = 0; j < input.size(); ++j) {
            V2F current = input[j];
            V2F last = input[(j + input.size() - 1) % input.size()];
            if (Inside(ViewLines[i], current.windowPos)) {
                if (!Inside(ViewLines[i], last.windowPos)) {
                    V2F intersecting = Intersect(last, current, ViewLines[i]);
                    output.push_back(intersecting);
                }
                output.push_back(current);
            }
            else if (Inside(ViewLines[i], last.windowPos)) {
                V2F intersecting = Intersect(last, current, ViewLines[i]);
                output.push_back(intersecting);
            }
        }
    }
    return output;
}

最后，在渲染流程中加入裁剪，因为裁剪后生成了新的顶点，所以要做比较多的修改：

// 画网格
void DrawMesh(const Mesh& mesh) {
    if (mesh.EBO.empty()) {
        return;
    }
    for (int i = 0; i < mesh.EBO.size(); i += 3) {
        Vertex p1, p2, p3;
        p1 = mesh.VBO[mesh.EBO[i]];
        p2 = mesh.VBO[mesh.EBO[i + 1]];
        p3 = mesh.VBO[mesh.EBO[i + 2]];

        // 顶点着色器变换到裁剪空间
        V2F v1, v2, v3;
        v1 = shader->VertexShader(p1);
        v2 = shader->VertexShader(p2);
        v3 = shader->VertexShader(p3);

        // 视锥体剔除
        UpdateViewPlanes();
        if (FrustumCull && !WorldFrustumCull(ViewPlanes, v1.worldPos / v1.w, v2.worldPos / v2.w, v3.worldPos / v3.w))
        {
            continue;
        }

        // 正面/背面剔除
        if (FaceCull && WorldFaceCull(CullMode, v1.worldPos, v2.worldPos, v3.worldPos))
        {
            continue;
        }

        // 裁剪空间剔除
        if (!ClipSpaceCull(v1.windowPos, v2.windowPos, v3.windowPos)) {
            continue;
        }
        // 裁剪
        std::vector<V2F> clipingVertexs = SutherlandHodgeman(v1, v2, v3);

        // 做透视除法，变换到NDC
        for (int i = 0; i < clipingVertexs.size(); ++i) {
            PerspectiveDivision(clipingVertexs[i]);
        }

        // 渲染
        int n = clipingVertexs.size() - 3 + 1;
        for (int i = 0; i < n; ++i) {
            V2F tempv1 = clipingVertexs[0];
            V2F tempv2 = clipingVertexs[i + 1];
            V2F tempv3 = clipingVertexs[i + 2];

            // 视口变换，变换到屏幕空间
            tempv1.windowPos = ViewPortMatrix * tempv1.windowPos;
            tempv2.windowPos = ViewPortMatrix * tempv2.windowPos;
            tempv3.windowPos = ViewPortMatrix * tempv3.windowPos;

            // 画线
            if (renderMode == Line) {
                DrawLine(tempv1, tempv2);
                DrawLine(tempv2, tempv3);
                DrawLine(tempv3, tempv1);
            }
            // 光栅化
            else {
                ScanLineTriangle(tempv1, tempv2, tempv3);
            }
        }
    }
}

这里为了能更方便看出裁剪效果，我们加入了渲染模式选项：

// 渲染模式
enum RenderMode {
    Line,    // 仅绘制边框
    Fill    // 绘制图形
};


// 改变渲染模式
void ChangeRenderMode()
{
    if (renderMode == Fill)
        renderMode = Line;
    else
        renderMode = Fill;
}

然后新增一个画线算法，使用 BresenhamLine 画线算法，原理比较简单，具体可以查看Bresenham 算法原理，代码如下：

/*
    ****************** BresenhamLine画线算法 *******************
*/
void DrawLine(const V2F& from, const V2F& to)
{
    int dx = to.windowPos.x - from.windowPos.x;
    int dy = to.windowPos.y - from.windowPos.y;
    int Xstep = 1, Ystep = 1;
    if (dx < 0)
    {
        Xstep = -1;
        dx = -dx;
    }
    if (dy < 0)
    {
        Ystep = -1;
        dy = -dy;
    }
    int currentX = from.windowPos.x;
    int currentY = from.windowPos.y;
    V2F tmp;
    //斜率小于1
    if (dy <= dx)
    {
        int P = 2 * dy - dx;
        for (int i = 0; i <= dx; ++i)
        {
            tmp = V2F::lerp(from, to, ((float)(i) / dx));
            FrontBuffer->WritePoint(currentX, currentY, glm::vec4(1, 0, 0, 1));
            currentX += Xstep;
            if (P <= 0)
                P += 2 * dy;
            else
            {
                currentY += Ystep;
                P += 2 * (dy - dx);
            }
        }
    }
    //斜率大于1，利用对称性画
    else
    {
        int P = 2 * dx - dy;
        for (int i = 0; i <= dy; ++i)
        {
            tmp = V2F::lerp(from, to, ((float)(i) / dy));
            FrontBuffer->WritePoint(currentX, currentY, glm::vec4(1, 0, 0, 1));
            currentY += Ystep;
            if (P <= 0)
                P += 2 * dx;
            else
            {
                currentX += Xstep;
                P -= 2 * (dy - dx);
            }
        }
    }
}

5 测试

现在来测试一下上面实现的裁剪吧，因为可以只渲染边框，可以清楚的看到每个面的渲染情况。

我们首先关闭背面剔除，得到的结果：

然后开启背面剔除：

试试开启正面剔除：

接下来将正方体移动到屏幕边缘，测试裁剪效果：

可以看到裁剪产生的新的图元。