本篇对《Real-Time Rendering》一书中的渲染加速技术进行概括总结和扩展。主要内容包括:
- 空间管理(BVH、BSP 树、八叉树、场景图)
- 裁剪技术(背面裁剪、视锥裁剪、遮挡剔除、层次视锥裁剪、入口裁剪、细节裁剪)
- 层次细节技术(LOD)
- 点渲染
1 空间管理
空间数据结构(Spatial Data Structures)是将几何体组织在 N 维空间中的一系列数据结构,而且我们可以很容易地将二维和三维的一些概念扩展到高维之中。这些空间数据结构可以用于很多实时渲染相关操作的加速查询中,如场景管理,裁减算法、相交测试、光线追踪、以及碰撞检测等。
空间数据结构的组织通常是层次结构的。宽泛地说,即最顶层包含它之下的层次,后者又包含更下层的层次,以此类推。因此,这种结构具有嵌套和递归的特点。用层次结构的实现方式对访问速度的提升很有帮助,复杂度可以从 O(n) 提升到 O(log n)。但同时,使用了层次结构的大多数空间数据结构的构造开销都比较大,虽然也可以在实时过程中进行渐进更新,但是通常需要作为一个预处理的过程来完成。
一些常见的空间数据结构包括:
- 层次包围盒(Bounding Volume Hierachy,BVH)
- 二元空间分割树(Binary Space Partitioning,BSP)
- 四叉树(QuadTree)
- kd 树(k-dimensional tree)
- 八叉树(Octree)
- 场景图(Scene Graphs)
其中,BSP 树和八叉树都是基于空间细分(Space Subdivision)的数据结构,这说明它们是对整个场景空间进行细分并编码到数据结构中的。例如,所有叶子节点的空间集合等同于整个场景空间,而且叶子节点不相互重叠。
层次包围盒不是空间细分结构,是对物体进行细分的结构,它仅将几何物体周围的空间包围起来,所以包围层次不需要包围所有的空间,但包围盒之间可以重叠。
而场景图是一种比较高层次的,相较渲染性能更关注模型关系的数据结构。
1.1 层次包围盒 BVH
对于三维场景的实时渲染来说,层次包围体(Bounding Volume Hierarchy,BVH)是最常使用的一种空间数据结构。例如,层次包围体经常用于层次视锥裁减。使用 BVH 的场景以层次树结构进行组织,包含一个根节点(root)、一些中间节点(internal nodes),以及一些叶子节点(leaves)。顶部的节点是根,其无父节点。叶子节点(leaf node)包含需渲染的实际几何体,且其没有子节点。
相比之下,中间节点包含指向它子节点的指针。因此,只要根节点不是这颗树唯一的一个节点,那么它就是一个内部节点。树中的每一个节点,包括叶子节点,都有一个包围体可以将其子树中的所有几何体包围起来,这就是包围体层次的命名来源,同时,也说明了根节点有一个包含整个场景的包围体。
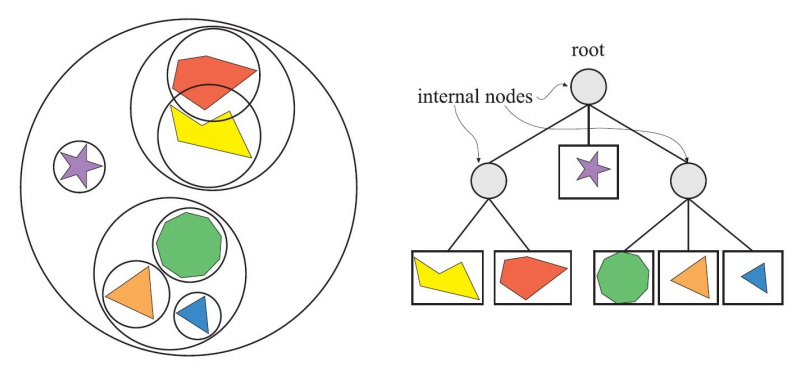
关于 BVH 的理论详述可以查看之前的笔记【计算机图形学】(十一)Whitted 风格光线追踪中的“交点计算加速”部分。而 BVH 的代码实现可以在【RayTracer】(十)实现 BVH中查看。
1.2 BSP 树
BSP 树(二叉空间分割树,全称 Binary Space Partitioning Tree)是一种常用于判别对象可见性的空间数据结构。类似于画家算法,BSP 树可以方便地将表面由后往前地在屏幕上渲染出来,特别适用于场景中对象固定不变,仅视点移动的情况。
其中,BSP 是 Binary SpacePartitioning(二叉空间划分法)的缩写。这种方法递归地将空间使用超平面划分为凸面体集合。而这种子划分引出了借助于称之为 BSP 树的树形数据结构的场景表示。
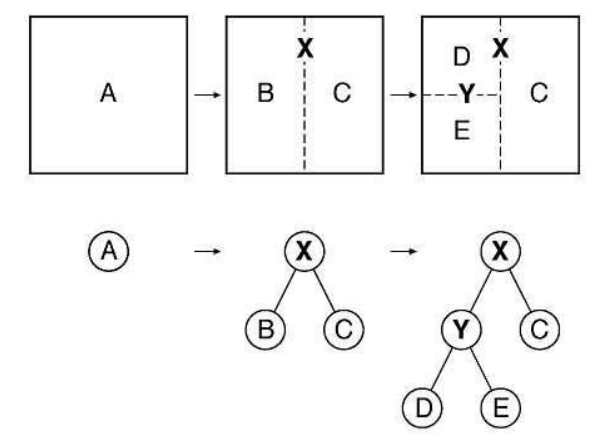
BSP 树是一棵二叉树,每个节点表示一个有向超平面,其将当前空间划分为前向(front)和背向(back)两个子空间,分别对应当前节点的左子树和右子树。BSP 树的一个有趣特性是,如果用一种特定的方式遍历,树的几何内容可以从任何角度进行前后排序。而 BVH 与之不同,因为 BVH 通常不包含任何形式的排序。
1.2.1 BSP 树的构建
- 从空树开始,每次选择一个面片作为节点插入树中
- 每次插入一个新节点,从树的根节点开始遍历
- 如果新节点面片与当前结点片面相交,将新面片分割成两个面片
- 新节点在当前节点前向空间,插入左子树
- 新节点在当前节点背向空间,插入右子树
- 当前节点为空,直接插入新节点
- 直到所有面片都被插入树中
简单来说,若要创建 BSP 树,需递归将一个平面空间一分为二,并将几何体归类到这两个空间中来完成。
1.2.2 BSP 树的遍历
从根节点开始,判断输入位置与当前分割平面的“前”、“后”关系,“前”则遍历左子树,“后”则遍历右子树,递归到叶子节点终止。
用平面方程 Ax + By + Cz + D = 0 判断前后位置,可用D(x0, y0, z0) = Ax0 + By0 + Cz0 + D 进行判别,其中:
- D > 0:在平面前面
- D = 0:在平面上
- D < 0:在平面后面
1.2.3 BSP 树的种类
在计算机图形学中,BSP 树有两大类别,分别是为轴对齐(Axis-Aligned)BSP 树和多边形对齐(Polygon-Aligned)BSP 树。下面分别进行介绍。
1.2.4 轴对齐 BSP 树
轴对齐 BSP 树可以按如下方式来创建。首先,将整个场景包围在一个 AABB(轴对齐包围盒,Axis-Aligned Bounding Box)中,然后以递归的方式将这个包围盒分为若干个更小的盒子。
现在,考虑一下任何递归层次的盒子。选取盒子的一个轴,生成一个与之垂直的平面,将盒子一分为二。有一些方法可以将这个分割平面固定,从而将这个盒子分为完全相同的两部分,而也有其他的一些方法,允许这个平面在位置上有一些变化。与分割平面相交的物体,要么存储在这个层次上,成为两个子集中的一员,要么被这个平面分割为两个不同的物体。
经过这个过程,每个子集就处于一个比较小的盒子中,重复这个平面分割的过程,就可以对每个 AABB 进行递归细分,直到满足某个标准才终止这个分割过程。而这个标准,通常是用户定义的树最大深度,或者是盒子里面所包含的几何图元数量,需低于用户定义的某个值。
分割平面的轴线和位置对提高效率至关重要。一种分割包围盒的方法就是轴进行循环。即在根节点,沿着 x 轴对盒子进行分割,然后再沿着 y 轴对其子盒子进行分割,最后沿 z 轴对其孙盒子进行分割。这样,就完成了一个循环周期。使用这种分割策略的 BSP 树常被称为 k-d 树。而另一种常见策略是找到盒子的最长边,沿着这条边的方向对盒子进行分割。
下图显示了一个 BSP 树的分割过程,可以直观理解上述过程:
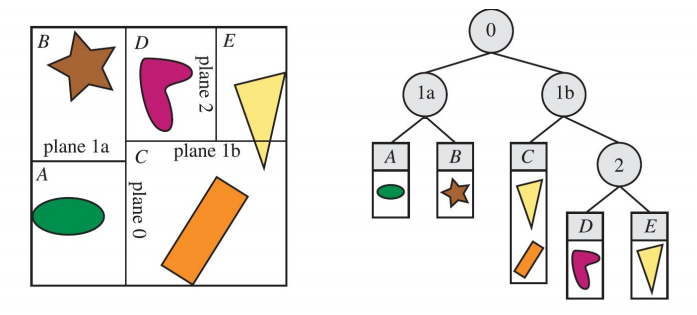
值得一提的是,从前到后的粗排序(Rough Front-to-Back Sorting)是轴对齐 BSP 树的一种应用示例,这种方法对于遮挡剔除算法非常有用。而在视点的另一侧进行遍历,可以得到从后向前的粗排序(Rough Fack-to-Gront Sorting),这对于透明排序非常有用。且还可以用来测试射线和场景几何体相交的问题,只需将视点位置换为射线原点即可,另外还可以用于视锥裁剪。
1.2.5 多边形对齐 BSP 树
多边形对齐 BSP 树(Polygon-aligned BSP tree)是 BSP 树的另一大类型,其中将多边形作为分隔物,对空间进行平分。也就是说,在根节点处,选取一个多边形,用这个多边形所在平面将场景中剩余多边形分为两组。对于与分割平面相交的多边形来说,沿着其中的交线将这个多边形分为两部分。然后,在分割平面的每个半空间中,选取另外一个多边形作为分隔物,只对这个分隔物所在平面的多边形进行继续分割,直到所有的多边形都在 BSP 树中为止。下图是一个多边形对齐 BSP 树的示意图:
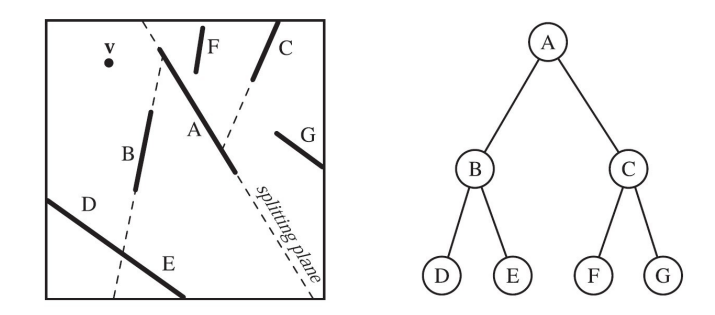
需要注意,多边形对齐 BSP 树的创建是一个非常耗时的过程,这些树通常只需计算一次,可以存储起来进行重用。另外,因为完全不平衡树的效率非常低,所以多边形对齐 BSP 树分割时最好是形成平衡树,即每个叶子节点的深度相同或者相差一个层次的树。
多边形对齐 BSP 树的一个典型性质就是对于一个给定的视点来说,可以对该结构按照从后往前(或者从前往后)的顺序进行严格遍历,而轴对齐的 BSP 通常只能给出粗略的排序顺序。所以,基于多边形对齐 BSP 树的此性质,建立了严格的前后顺序,可以配合画家算法来绘制整个场景,而无需 Z 缓冲。多边形对齐 BSP 树的其他应用也包括相交测试和碰撞检测等。
1.3 八叉树
1.3.1 普通八叉树
八叉树(octree),或称八元树,是一种用于描述三维空间的树状数据结构。八叉树的每个节点表示一个正方体的体积元素,每个节点有八个子节点,这八个子节点所表示的体积元素加在一起就等于父节点的体积。一般中心点作为节点的分叉中心。
简单来说,八叉树的空间划分方式很简单,即递归地进行规整地 1 分为 8 的操作。如下图,把一个立方体分割为八个同样大小的小立方体,然后递归地分割出更的小立方体。这个就是八叉树的命名来源。这种分割方式可以得到比较规则的结构,从而使得查询变得高效。
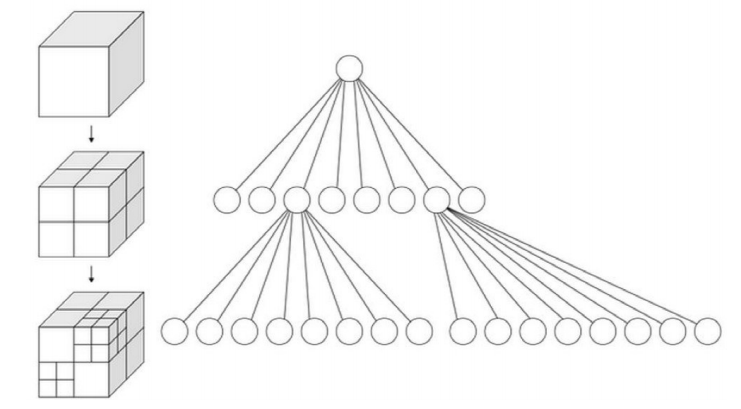
相似地,四叉树是把一个二维的正方形空间分割成四个小正方形。而八叉树是四叉树的三维空间推广。
1.3.2 松散八叉树
松散八叉树(Loose Octrees)的基本思想和普通八叉树一样,但是每个长方体的大小选择比较宽松。如果一个普通长方体的边长为 a,那么可以用 ka 来代替,其中 k > 1,如下图所示:
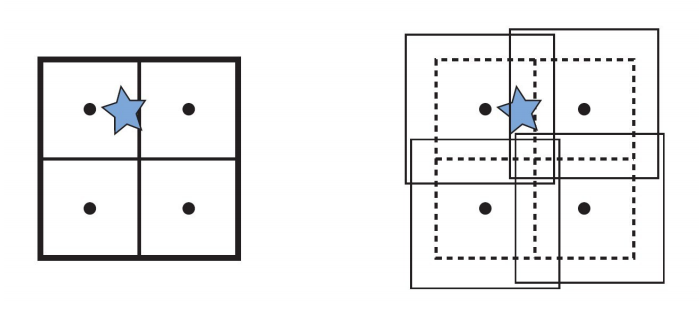
上图是一个普通八叉树和松散八叉树的比较。图中黑色的原点表示长方形的中心点(第一次细分)。在左图中,星形物体刺穿了一个普通八叉树的一个分割平面。这时,一种选择就是将这个星型物体放在最大的长方形中(根节点的长方体)。而右图所示为一个 k=1.5 的松散八叉树,也就是将细分的长方体放大了 50%,如果将这些长方体稍微移动,就可以保证区分出们。这样,这个星形多边形就完全位于左上角的长方形之中。
1.4 场景图
BVH、BSP 树和八叉树都是使用某种形式的树来作为基本的数据结构,它们的具体区别在于各自是如何进行空间分割和几何体的存储,且他们均是以层次的形式来保存几何物体。然而三维场景的绘制不仅仅是几何体。对动画,可见性,以及其他元素的控制,往往需要通过场景图(Scene Graphs)来完成。
场景图被誉为“当今最优秀且最为可重用的数据结构之一“。Wiki 中对场景图的定义是:
场景图(Scene Graph)是组织和管理三维虚拟场景的一种数据结构,是一个有向无环图(Directed Acyclic Graph, DAG)。
场景图是一个面向用户的树结构,可以通过纹理、变换、细节层次、渲染状态(例如材质属性)、光源以及其他任何合适的内容进行扩充。它由一棵以深度优先遍历来渲染整个场景的树来表示。
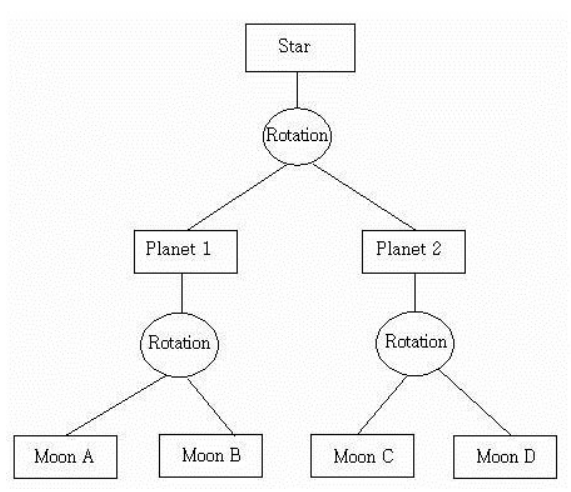
开源的场景图有 Open Scene Graph 和 OpenSG 等。
2 裁剪技术
裁剪(Culling)的字面意思是“从大量事物中进行删除”。在计算机图形学中,相对应的就是裁剪技术(Culling Techniques)所要做的工作——“从大量游戏事物中进行删除”。所谓的“大量事物”就是需要绘制的整个场景,删除的是对最终图像没有贡献的场景部分,然后将剩余场景发送到渲染管线。因此,在渲染方面通常使用“可见性裁剪 (Visibility Culling)”这个术语。但其实,裁剪也可以用于程序的其他部分,如碰撞检测(对不可见物体进行不十分精确的计算)、物理学计算,以及人工智能(AI)领域。
与渲染相关的裁剪技术,常见的有:
- 背面裁剪(Backface Culling):将背向视点的物体删除,是一种非常简单直观的操作,只能一次对一个单一多边形进行操作。
- 视锥裁剪(View Frustum Culling):将视锥之外的多边形删除,相对而言,这种操作比背面裁剪稍微复杂。
- 遮挡剔除(Occlusion Culling):将被其他物体遮挡的物体进行删除,这种操作在三者中最为复杂,因为其需要聚集一个或者多个物体,同时还需使用其他物体的位置信息。
理论上,裁剪操作可以发生在渲染管线的任何一个阶段,而且对于一些遮挡裁剪算法来说,甚至可以预先计算出来。对于在硬件中实现的裁剪算法来说,有时只需启动/禁止或者设置一些裁剪函数即可。而为了进行完全控制,我们可以在应用程序阶段在(CPU 上)实现一些裁剪算法。裁剪通常可以使用几何计算来实现,但也不局限于此。
下图展示了三种裁剪技术:
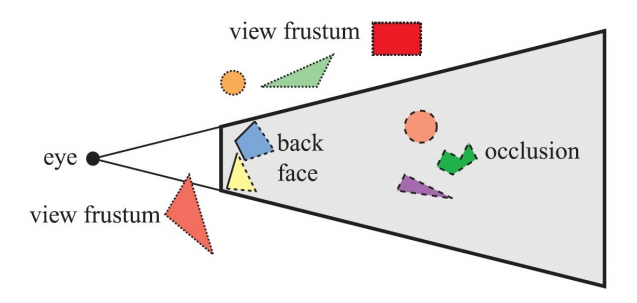
2.1 背面裁剪
假设你正在观察一个场景中不透明的球体。大约有一半的球体是不可见的。那么,可以从中这个例子里得到一个众所周知的结论,那就是,对不可见的内容不需要进行渲染,因为它们对最终的渲染图像没有贡献。不需要对球体的背面进行处理,这就是背面裁剪的基本思想。对于一组物体来说,还可以一次性地进行背面裁剪,这也称为聚集背面裁剪(Clustered Backface Culling)。
背面裁剪有屏幕空间和观察空间两种方法,如下图所示:
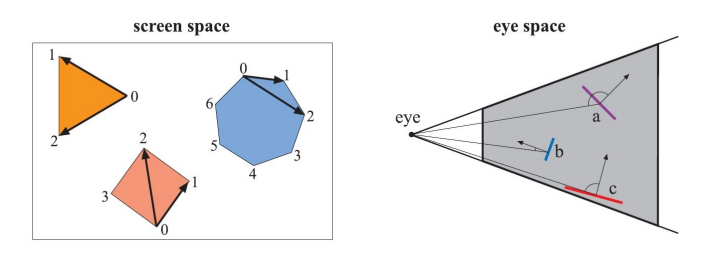
左图为屏幕空间背面裁剪,使用叉乘运算。根据右手定则可以判断出三角形和四边形是正面,七边形是背面,背面的多边形无需进行光栅化。
右图为观察空间背面裁剪,使用点乘运算。根据表面法线和视线夹角判断正面还是背面。
2.2 层次视锥裁剪
众所周知,只需对完全或者部分在视锥中的图元进行渲染。一种加快渲染速度的方法便是将每个物体的包围体与视锥进行比较,如果包围体位于视锥之外,那么便不需要渲染包围体中的几何体。由于这些计算在 CPU 上进行,因此包围体中的几何体不需要通过管线中的几何和光栅阶段。相反,如果包围体在视锥内或者与视锥相交,那么包围体中的内容就是可见的,所以必须发送到渲染管线中去。
利用空间数据结构,可以分层地来应用这种裁剪。例如,对于层次包围盒 BVH 来说,从根节点进行前序遍历(Preorder Transversal),就可以完成这一任务。
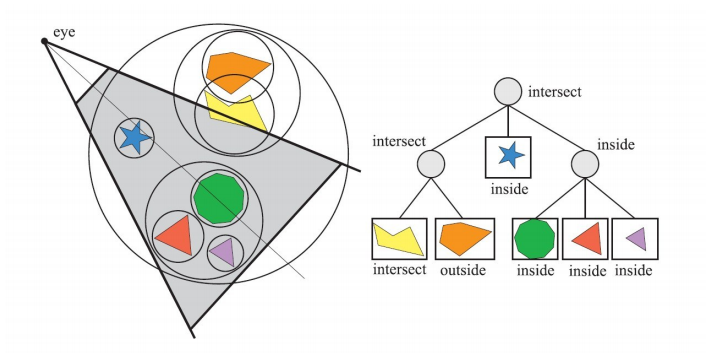
视锥裁剪操作位于应用程序阶段(CPU),这意味着几何阶段和光栅阶段都可以从中受益,对于大场景或者一定的相机视线来说,场景只有一小部分是可见的,只需要将这部分发送到渲染管线。可期望获得一定的加速效果,视锥裁剪技术利用了场景中的空间相关性,因为可以将彼此靠近的物体包围在一个包围盒中,而且几乎所有包围盒都是以层次形式聚集在一起。
除了层次包围盒,其他的空间数据结构同样也可以用于视锥裁剪,包括上文提到的八叉树和 BSP 树。但是当渲染动态场景时,这些方法便会显得不够灵活,不如层次包围盒。
2.3 入口裁剪
对建筑物模型来说,很多裁剪方面的算法可以归结为入口裁剪(Protal Culling)。入口裁剪算法的基本思想是,在室内场景中,建筑物墙面通常充当大的遮挡物,通过每个入口(如门或者窗户)进行视锥裁剪,只对穿过入口能看到的几体体进行渲染。当遍历入口的时候,就减小视锥,使得与入口尽可能紧密贴合。因此,可以将入口裁减算法看作是视锥裁剪算法的一种扩展,且需将位于视锥之外的入口丢弃。
入口裁剪方法以某种方式对场景进行预处理,可以是自动形式,也可以是手动形式,可以将场景分割为一系列单元(Cells),其通常对应于建筑物中的房间或者走廊;房间的门和窗口称为入口(Protals)。单元中的每个物体和单元的墙面可以存储在一个与单元关联的数据结构中,还可以将邻接单元和链接这些单元的入口信息保存在一个临接图中。
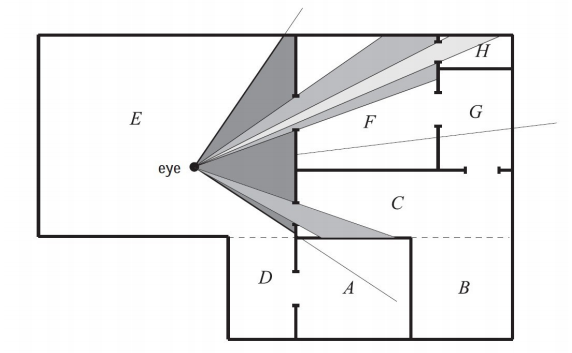
2.4 细节裁剪
细节裁剪(Detail Culling)是一种通过牺牲质量换取速度的技术。其基本原理是,当视点处于运动的时候,场景中的微小细节对渲染出的图像贡献甚微。且当视点停下来的时候,通常禁止细节裁剪。
考虑一个具有包围体的问题,将这个包围体投射到投影平面,然后以像素为单位来估算投影面积,如果像素的数量小于用户定义的阈值,那么不对这个物体进行进一步处理。基于这个原因,细节裁剪也往往被称为屏幕尺寸裁剪(Screen-Size Culling)。另外,细节裁剪也可以在场景图上以层次形式来实现,几何阶段和光栅阶段都可以从这个算法中受益。
细节裁剪还可以作为一种简化的 LOD 技术来实现,其中一个 LOD 是整个模型,另外一个 LOD 是空物体。
2.5 遮挡剔除
可见性问题可以通过 Z 缓冲器的硬件构造来实现,即使可以使用 Z 缓冲器正确解决可见性问题,但其中 Z 缓冲并不是在所有方面都不是一个很“聪明”的机制。例如,假设视点正沿着一条直线观察,其中,在这条直线上有 10 个球体,虽然这 10 个球体进行了扫描转换,同时与 Z 缓冲器进行了比较并写入了颜色缓冲器和 Z 缓冲器,但是这个从这个视点渲染出的图像只会显示一个球体,即使所有 10 个球体都将被光栅化并与 Z 缓冲区进行比较,然后可能写入到颜色缓冲区与 Z 缓冲区。下图中间部分显示了在给定视点处场景的深度复杂度,深度复杂度指的是对每个像素重写的次数。对于有 10 个球体的情形,最中间的位置,深度复杂度为 10,因为在这个地方渲染了 10 个球体(假设背面裁剪是关闭的),而且这意味着其中有 9 次像素写入是完全没有必要的。
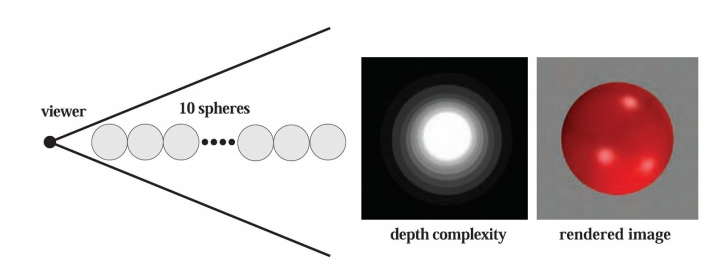
像上图这样无聊极端的场景,现实生活中很难找到,但其描述的这种密集性很高的模型的情形,在现实生活中却很常见,如热带雨林,发动机,城市,以及摩天大楼的内部。如下图:
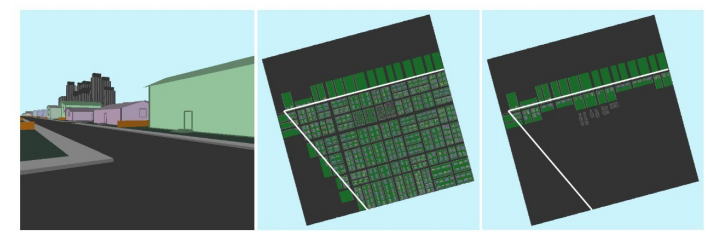
左图和中图为视锥裁剪后的图示,右图所示为遮挡剔除和视锥裁剪后的图示。
有两种主要形式的遮挡裁剪算法,分别是基于点的遮挡裁剪和基于单元的遮挡裁剪。如下图所示:
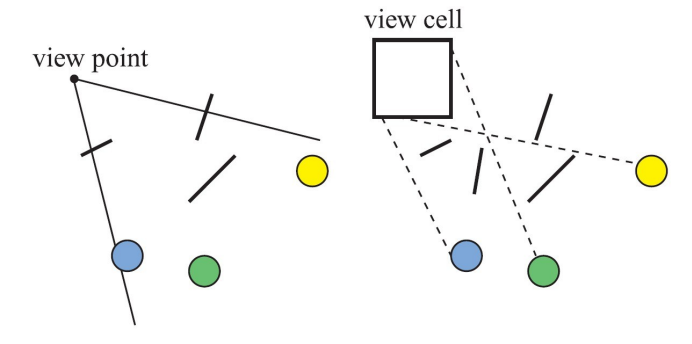
左图所示为基于点的可见性,右图所示为基于单元的可见性,其中单元是一个长方形,从中可以看出,从视点左边看上去,有些圆被遮挡了,但是从右边看上去,这些圆却是可见的,因为可以从单元的某个位置到这些圆画一些射线,这些射线没有和任何遮挡物相交。
2.5.1 硬件遮挡查询
现代 GPU 可以以一种特殊的渲染模式来支持遮挡剔除。通过硬件遮挡查询(Hardware Occlusion Queries),我们能够直接获得所提交的物体是否被绘制到场景中。
简单来说,硬件遮挡查询的基本思想是,当和 Z 缓冲器中内容进行比较时,用户可以通过查询硬件来找到一组多边形是否可见的,且这些多边形通常是复杂物体的包围体(如长方体)。如果其中没有多边形可见,那么便可将这个物体裁剪掉。硬件实现对查询的多边形进行光栅化,并且将其深度和 Z 缓冲器进行比较。
2.5.2 层次 Z 缓冲
层次 Z-缓冲算法(Hierarchical Z-Buffering,HZB)对遮挡剔除的研究有着显著的影响。尽管其在 CPU 上很少使用,但该算法是 GPU 上做 Z-Culling(深度裁剪)的基础。
层次 Z-缓冲算法用八叉树来维护场景模型,并将画面的 Z 缓冲器作为图像金字塔(也称为 Z-金字塔,Z-pyramid),该算法因此在图像空间中进行操作。其中,八叉树能够对场景的遮挡区域进行层次剔除,而 Z-金字塔则可以对单个基元和边界体积进行层次 Z 缓冲。因此 Z-金字塔可以作为此算法的遮挡表示。
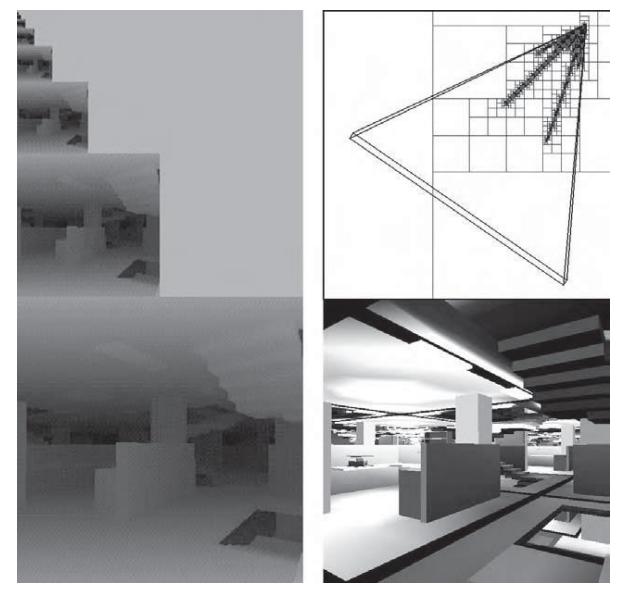
使用 HZB 算法的遮挡裁剪示例,显示了一个复杂的场景(右下),相应的 Z-pyramid(左图),以及八叉树细分(右上)。通过从前到后遍历八叉树并裁剪遇到的八叉树节点,此算法可以仅访问可见的八叉树节点及其子节点(右上角的节点),的容器只对可见包围体中的多边形进行渲染。在这个例子中,遮挡八叉树节点的裁剪可以将深度复杂度从 84 降低到了 2.5。
3 层次细节技术
细节层次(Level of Detail,LOD)的基本思想是当物体对渲染出图像贡献越少,使用越简单的形式来表达该物体。这是一个已经在各种游戏中广泛使用的基本优化技术。
例如,一个包含一百万个三角形的汽车,其中所包含的细节信息比较丰富。当视点靠近物体时,可以使用详细的细节表示,而当视点远离物体时,比如仅需覆盖 200 个像素,则完全无需渲染出一百万个三角形,相反,我可以使用诸如只有 1000 个三角形的简化模型。而由于距离的原因,简化后的模型与细节较丰富的模型看上去其实很接近。以这种方式,可以显著地提高渲染的性能开销。

通常情况下,雾效会与 LOD 一起使用。这样我们可以完全跳过对一些物体的渲染,直接用不透明的雾来进行遮挡。
一般情况下,完整的 LOD 算法包含 3 个主要部分:
- 生成 Generation:生成不同细节的模型表示,可以使用算法,也可以手工制作具有不同数量的三角形模型
- 选择 Selection:基于某种准则选取一个层次细节模型,比如屏幕上的评估面积
- 切换 Switching:从一个细节层次转换到另一个细节层次
3.1 LOD 的切换方法
当从一个 LOD 切换到另一个 LOD 的时候,忽然的模型替换往往会引起观察者的注意。这种现象被称为突越(Poping)。这里有几种不同的 LOD 切换方法,有着不同的特性。
3.1.1 离散几何 LOD
离散几何 LOD 是最简单的 LOD 算法,不同的表示是不同图元数量的同一模型,但这种方法突越现象严重。
3.1.2 混合 LOD
在概念上,完全可能存在一种直观的方法,从一个 LOD 切换到另一个 LOD,只需要在较短的时间内在两个 LOD 之间执行一个线性混合,这种方法无疑可以得到一种比较平滑的切换,但是这种混合操作的代价较高。渲染两个 LOD 要比一个 LOD 需要更大开销,因此也就违背了 LOD 的初衷。但 LOD 切换通常发生在较短时间内容,在同一时间也不是对场景中所有物体进行切换,所以依然可以从中获益。
3.1.3 透明 LOD
完全避免突越现象的一种简单方法便是使用 alpha LOD。其中并没有使用同一物体很多不同细节的实例,而且每个物体只有一个实例。随着 LOD 选取度量值(如与物体之间的距离)的增大,物体整体透明度也随之增大(也就是 alpha 值减小),当完全透明时,物体最终就会消失。这种方法的优点是,比离散几何 LOD 方法上感觉更连续一些,可以避免突跃现象。此外,由于物体最终会完全消失而不需要进行渲染,可以得到很好的加速效果。
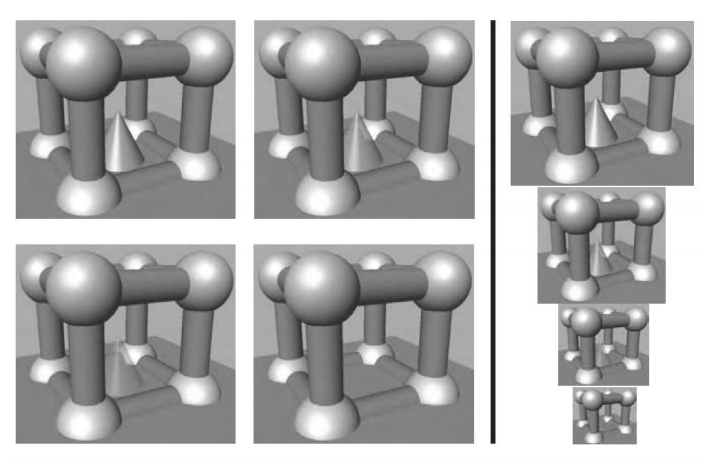
使用 Alpha LOD 对图中的圆锥体进行渲染,当距离圆锥体较远时,就提高它的透明度,直到最后消失。直线左边的图像是从同一距离处进行的观察,而直线右边的图像是左边图像不同尺寸的情形。
3.1.4 连续 LOD 和几何形变 LOD
连续细节层次(Continuous Level of Detail , CLOD)的基本思想是基于 LOD 选取值来精确决定可见多边形的数量。在 100m 远处,模型包含 1000 个多边形,当移动的到 101m 的地方时,模型减少到 998 个多边形。
几何形变层次细节(Geomorph LODs)是基于简化生成的一组离散模型,且其中模型顶点之间的链接关系保持不变。关于GLODs 可以查看之前的笔记【计算机图形学】(九)几何中的表面简化方法。
3.2 LOD 的选取方法
给定一个物体不同细节层次,必须做一个选择,决定渲染或者混合其中的哪一个层次,这就是 LOD 选择(LOD selection)的任务。有几种不同的 LOD 选择方案,这些方案也可以用于遮挡剔除算法。
3.2.1 基于距离的 LOD 选取
原理如下图所示:
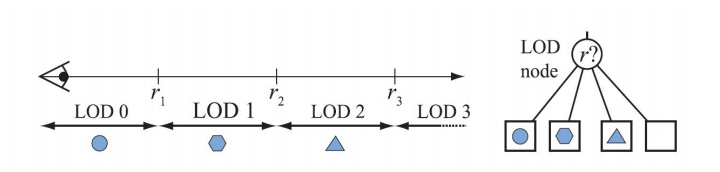
3.2.2 基于投影面积的 LOD 选取
基于投影面积的 LOD 选取,顾名思义,即投影面积越大,就选取细节越丰富的 LOD。
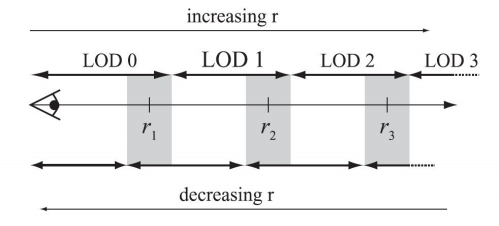
3.2.3 基于滞后的 LOD 选取
若用于确定 LOD 度量标准围绕某个值 ri 在画面之间是变化的,那么就会出现不必要的突跃现象,也就会在不同的 LOD 之间来回快速切换。对此,可以引入一个围绕 ri 值的滞后来解决这个问题。如下图,这是一个基于距离的 LOD,可以应用于任何类型,当 r 增大时,使用上一行的 LOD 距离;当 r 减小时,使用下面一行的 LOD 距离。
4 点渲染
点渲染的基本思想是用一个大的点集来表示物体表面并予以渲染。在随后的通道中,使用高斯滤波来填充渲染点之间的间隙。而高斯滤波器的半径取决于表面上点的密度和屏幕上的投影密度。知道有这种渲染方法即可,不必深究。