【Real-Time Rendering】程序噪声总结

上一篇提到过，程序纹理基本上都是通过噪声纹理来实现的，不同的噪声纹理适合制作不同的效果，如云雾、水波、大理石、能量波等。这一节对常见的程序噪声算法进行总结，主要包括：

Value Noise
Gradient Noise（Perlin Noise、Simplex Noise）
Voronoi Noise 和 Worley Noise
Fractal Brownian Motion
Curl Noise
White Noise

1 噪声概述

对于图形学而言，噪声通常会用作程序化效果生成（如地形、水面、云层等），其最开始在图形学中引进，是为了代替贴图给物件添加纹理以解决电脑内存不足的问题（不过噪声的计算通常比贴图采样要慢一点，因此现在通常是直接使用噪声贴图来代替 shader 的随机数计算），但是并不是所有的噪声都是有用的，只有那些数据具有一定的连贯性的噪声才算是有用的噪声，而如果噪声不连贯的话，在进行贴图采样后，得到的结果就会呈现一种混乱的状态，这种对于程序化生成而言并没有什么作用，因此图形学中的一个理想的噪声应该具备如下几个特性：

伪随机（不变性）：所谓的噪声只是看起来随机而已，实际上，需要保证在同样的输入下，肯定能够得到同样的输出，否则可能出现渲染的结果随着时间或者观察位置而变化，这就不够物理了，而且结果不可控也跟实际需要不符合。
只返回一个 float 值，不管输入是几维的，只返回一个 float。
噪声通常是带限的（band-limited），噪声频率过高通常会导致锯齿（镜头旋转等情况下常见），因此通常其频率范围都是有限的，不过对于一些平缓（大尺寸）变化的情形需要一些低频噪声，而对于一些细节变化则需要一些高频噪声。
噪声需要具有一定的连续性，比如某些情况下需要计算噪声的导数，甚至需要计算高阶微分，因此对于噪声的连续性有一定的要求。
四方连续，为了保证 tiling 时不会出现肉眼可辩的缝隙，需要保证上下左右四个方向都是连续的（如果使用了大量 tiling 可能会导致重复纹样，而解决重复的做法就是将 tiling 尺寸设得足够大，虽然可能会引入其他问题，但是这个问题可以通过其他方式来规避）。

2 Value Noise

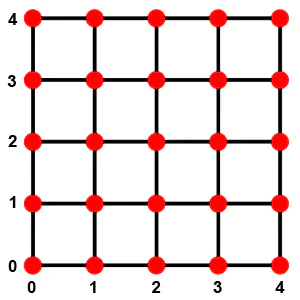
Value Noise 是最简单的一类噪声，其实现算法非常简单，以 2D 为例，我们在一个规整的 2D 网格上的每个顶点（如下图中的每个红色小圆点）放置一个随机数（通常范围在 [0, 1] 之间），之后使用线性插值填充每个小方格，得到的结果就是 Value Noise。

3 Gradient Noise

Value Noise 是通过对周边顶点的随机 Value 进行插值来得到噪声贴图的，而 Gradient Noise 的实现原理与 Value Noise 类似，不同的是，这里是通过对周边顶点的 Gradient（梯度，可以理解为某个点的速度，常用向量来表示）进行插值来输出噪声贴图。

对梯度进行插值，这里有一个问题需要解决，那就是对向量的插值，得到的结果肯定还是向量，而前面说过，噪声的输出结果应该是一个浮点数，那么要怎么实现这二者的转换呢？这里的做法是将当前像素点到对应顶点的连线作为一个向量，与这个顶点的梯度进行点乘，就得到了对应的浮点数，之后再对这个浮点数应用与 Value Noise 一样的插值算法，就能得到对应的噪声结果了。

根据插值顶点选取算法的不同，这里又有不同的细分，Perlin Noise 与前面的 Value Noise 类似，都是选取周边四个顶点（如果是 3D 的，就是周边 8 个顶点，以此类推）的数据进行插值，而 Simplex Noise 则不同，选取的是等边三个顶点的数据（如果是 3D，选取的就是正四面体的四个顶点进行插值），下面来看这两种噪声的实现细节。

3.1 Perlin Noise

Perlin Noise 非常常见，关于 Perlin Noise 可以查看之前在光线追踪中的实现：【RayTracer】（十二）Perlin 噪声。

3.2 Simplex Noise

实际上，Simplex 噪声跟 Perlin 噪声都是 Ken Perlin 发明的，后者是对前者的优化替代，Simplex 实际上是一种算法，既可以用于实现 Value Noise，同样也可以用于实现 Gradient Noise，不过由于 Gradient Noise 的应用范围更广，因此这里我们就直接跳过 Value Noise 部分，只介绍用于实现 Gradient Noise 的部分。

Simplex Noise 与 Perlin Noise 的区别在于其插值时所选取的周边顶点的算法不同，具体而言，是选取此像素所从属的 grid 中的正三角形（等边三角形）的三个顶点（即将 Perlin Noise 中的插值正方形沿着对角线一分为二，选取当前像素所在的那个正三角形的三个顶点，对应到 3D 空间，Perlin 使用的是立方体的 8 个顶点，而 Simplex 使用的则是连接相邻三个面的对角线组成的四面体转换后的正立方体的四个顶点）作为插值的数据源。

相对 Perlin Noise，Simplex 的实现更为简洁，其成本也更低。与前面计算某个像素对应的噪声值需要通过对周边顶点数据进行插值不同，Simplex 采用的是衰减函数，比如根据某个顶点到此像素的距离来计算此顶点数据对于此像素的贡献，之后将周边顶点的贡献进行累加就得到了最终的输出结果。

前面说到，Simplex 噪声来自于正三角形（正四面体）的数据衰减，那么这个正三角形是怎么来的呢？我们知道，一个 2D 平面，既可以使用正方形进行无缝平铺，这种 tiling 方式对应的就是前面 Value / Perlin Noise 的计算基础，同时也可以使用正三角形进行平铺，而这对应的则是 Simplex 噪声的实现基础，这里的一个问题就是这二者是如何转换的，毕竟我们平常使用的基本上都是 grid，也就是正方形的平铺方式。这个转换过程可以参考：

图形学中常见噪声生成算法综述中的 2.2 节
Simplex noise - Wikipedia

4 Voronoi Noise 和 Worley Noise

Voronoi Noise 与 Worley Noise 在形态上十分相似，在图形学中的应用也基本一致，比如同样用于进行云层创建，水底焦散现象模拟等，那同样的噪声为什么会有两个名字呢？实际上图形学中最开始使用的是 Voronoi 噪声，只是这种噪声的实现算法消耗比较高，后面 Steven Worley 对齐进行了改进，提出了以其名字命名的 Worley 噪声。下面我们一起来看一下这两种噪声的实现算法。

Voronoi 噪声是通过在空间中生成随机分布的多个特征点，之后对于每个需要计算的像素，对所有的特征点进行遍历，找到距离其最近的特征点，以其对应的特征值作为此像素的值进行输出。下图展示了 Voronoi 噪声的生成过程：

Voronoi 噪声的思路很简单，但是由于需要对每个特征点进行遍历，整个算法的复杂度就变得很高了，为了降低计算的消耗，Worley 噪声就应运而生了。

Worley 噪声是通过将空间（2D / 3D）划分成一个个的 cell（正方形 / 立方体），在每个 cell 中的随机位置随机生成一个特征点，之后对于每个待计算的像素，搜寻周边的 cell，找到距离其最近的噪点，之后以距离此噪点的距离作为当前像素的噪声结果，就得到了对应的 Worley 噪声。相对于 Voronoi 噪声，Worley 算法的改进点在于将搜寻范围从所有特征点限定在了周边的若干个 cell 之中，理论上最正确的搜索范围是周边 25 个 cell，但实际上如果噪声函数选取得当，使用九宫格进行搜索也能得到正确的结果。下图展示了 Worley 噪声的结果：

如果将搜索范围换成 9 个 cell，会发现结果会存在异常，这是因为在某些随机函数作用下，九宫格搜索会漏掉一些正确解导致：

5 Fractal Brownian Motion

有时候单一频率的噪声不足以满足需求，会需要使用多级噪声累加的结果来实现程序化生成，这种方式我们称之为分形布朗运动（Fractal Brownian Motion，简称 FBM），也称为 Turbulence，简单来说就是将多个不同频率的噪声按照不同的振幅进行混合，在【RayTracer】（十二）Perlin 噪声中有 Turbulence 应用于 Perlin Noise 的代码实现。还可以将 FBM 应用于 Worley 噪声，得到的效果：

6 Curl Noise

Curl 噪声在图形学中有着广泛的应用，比如可以用于对粒子位置进行调制，使之产生卷曲的效果；比如可以对烟雾水流效果进行调制，生成湍流扰动效果等。相对于其他的流体模拟算法，Curl Noise 的生成算法算是十分简单的，但是应用起来效果却并没有减色多少。

Curl 噪声中的 Curl 可以看成是跟加减乘除号同等的一种运算符号，其输入数据是一个向量，经过 curl 运算之后，就得到了一个 divergence free（无散度）的向量场，这里先介绍下什么是向量的 divergence，即散度：
$$
div\ \vec a = \nabla · \vec a = \frac{\partial a_x}{\partial x} + \frac{\partial a_y}{\partial y} + \frac{\partial a_z}{\partial z}
$$
散度指的是向量三个分量在对应坐标轴方向上的偏微分之和，从物理上来说，指的是一个向量场在某个给定的位置散开或者说收敛的程度，日常生活中常见的流体比如水流，空气，烟雾等都是 divergence-free（无散）的。curl 噪声从物理上来说，可以用来表征用于对向量进行转向的力的大小。

下面我们来介绍一下 Curl 噪声的实现算法，对一个潜在的 3D 向量场 $\Psi$ 而言，令：
$$
\vec \Psi = (\Psi_1, \Psi_2, \Psi_3)
$$
由此我们可以计算出其 Curl Velocity 算子：
$$
\vec v(x,y,z) = (\frac{\partial \Psi_3}{\partial y} - \frac{\partial \Psi_2}{\partial z},
\frac{\partial \Psi_1}{\partial z} - \frac{\partial \Psi_3}{\partial x},
\frac{\partial \Psi_2}{\partial x} - \frac{\partial \Psi_1}{\partial y})
$$
2D 情况较为简单：
$$
\vec v(x,y) = (\frac{\partial \Psi}{\partial y},-\frac{\partial \Psi}{\partial x})
$$
根据流体力学可知，上述速度场都是无散的，即：
$$
\nabla·\vec v = 0
$$
具体来说，假设我们以二维 Perlin 噪声作为向量场，那么最终的 Curl 噪声就可以用如下公式表示：
$$
\vec v(x,y) = (\frac{PerlinNoise(x,y)}{\partial y},-\frac{PerlinNoise(x,y)}{\partial x})
$$
代码如下：

vec2 curlNoise(vec2 uv)
{
    float eps = 0.00001;
    float x = uv.x;
    float y = uv.y;
    //Find rate of change in X direction
    int firstOctave = 3;
    int accumOctaves = 3;
    bool revertPerlin = false;
    float n1 = perlin2DNoise(vec2(x, y + eps), revertPerlin).x;
    float n2 = perlin2DNoise(vec2(x, y - eps), revertPerlin).x;
    //Average to find approximate derivative
    float a = (n1 - n2)/(2.0 * eps);

    //Find rate of change in Y direction
    float n3 = perlin2DNoise(vec2(x + eps, y), revertPerlin).x;
    float n4 = perlin2DNoise(vec2(x - eps, y), revertPerlin).x;
    //Average to find approximate derivative
    float b = (n3 - n4)/(2.0 * eps);

    //Curl
    return vec2(a, -b);
}