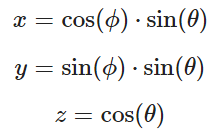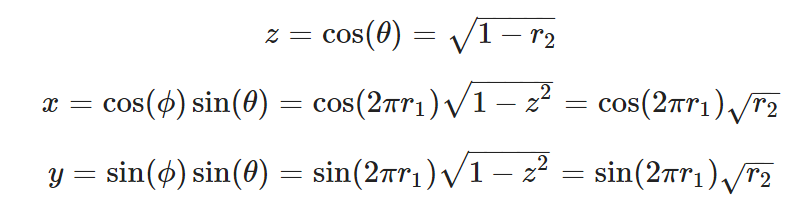【RayTracer】（十九）随机方向

上一节我们实现了基于蒙特卡洛积分的渲染方程并了解了重要性采样在光线追踪中的作用。这一节我们根据不同的概率密度来直接生成随机方向。经过上一节的推导，我们知道了之前实现的散射函数中的随机方向对应的概率密度是什么，但是没有显式的用概率密度去直接产生随机方向，而是用一个均匀分布（单位球面上随机取点）加上一个法线偏移达到这样的效果。这一节我们来实现直接生成给定概率密度的随机方向。

1 相对于 Z 轴的随机方向

我们先实现相对于 Z 轴的随机方向，也就是假设所有着色点的法线都是 Z 轴，之后再将他们转换到真实法线方向上。

在之前的推导中我们知道，球面上的随机方向的概率密度是和俯仰角 $\theta$ 有关的，对于给定的随机方向概率密度 $p(direction)=f(\theta)$，方位角和俯仰角的一维概率密度函数为：
$$
p(\phi) = \frac{1}{2\pi},\ p(\theta) = 2\pi f(\theta)sin\theta
$$
对于两个均匀生成的随机数 $r_1$ 、$r_2$，有：
$$
r_1 = \int_0^\phi \frac{1}{2\pi} dt
$$
可以求得：
$$
\phi = 2\pi r_1
$$
同理：
$$
r_2 = \int_0^\theta2\pi f(t)sin(t)dt
$$
之前推到过， lambertian 材质的散射光线的概率密度函数为：
$$
p(direction)=f(\theta)=\frac{cos\theta}{\pi}
$$
代入上式中得：
$$
r_2 = \int_0^\theta2\pi \frac{cost}{\pi}sin(t)dt=1-cos^2\theta
$$
于是可以求得：
$$
cos\theta = \sqrt{1-r_2}
$$
极坐标和直角坐标的转换公式为：

将解出来的 $\phi$ 和 $\theta$ 带入得到：

于是我们可以实现该函数：

// 生成概率分布为cos(theta)/pi的随机方向
inline vec3 random_cosine_direction() {
	auto r1 = random_double();
	auto r2 = random_double();
	// 方向是单位向量，所以z坐标就是cos(theta)
	auto z = sqrt(1 - r2);

	auto phi = 2 * pi * r1;
	auto x = cos(phi) * sqrt(r2);
	auto y = sin(phi) * sqrt(r2);

	return vec3(x, y, z);
}

我们可以利用这个方法生成其他概率分布的随机方向，只要替换推导过程中的 $f(\theta)$ 即可，比如均匀半球分布 $\frac{1}{2\pi}$，均匀球面分布 $\frac{1}{4\pi}$ 等。

2 相对于法线的随机方向

接下来我们将上面生成的围绕 z 轴的随机方向转换为围绕着色点法线的随机方向。这实际上就是一个坐标系转化的过程，回顾最简单的线性代数知识，向量 (x, y, z) 表示的是三个方向上的标准正交基的和，标准正交基就是一个坐标系的三个坐标轴，由于向量只有方向，没有位置，因此用这三个数组合任意的标准正交基都可以得到这个标准正交基下的一个向量，所以我们只要求出法线所在的坐标系下的三个标准正交基，再用 (x, y, z) 组合，就可以得到法线坐标系下的随机方向了。

得到法线坐标系的标准正交基很简单，类似于之前相机类中实现的方法，我们可以随机选一个不平行于法线 $\vec n$ 的向量 $\vec a$，二者叉乘得到一个向量 $\vec t$，再用 $\vec t$ 和法线 $\vec n$ 叉乘得到向量 $\vec s$，则 $\vec n$ 、 $\vec s$ 、 $\vec t$ 就构成一组标准正交基。

至于随机选一个不平行于法线 $\vec n$ 的向量 $\vec a$，我们可以直接给定 $\vec a$ 就是 (1, 0, 0)，为了保证不和法线平行，当法线接近 (1, 0, 0) 的时候， $\vec a$ 就改为 (0, 1, 0)。

标准正交基的实现如下：

/*
* 标准正交基Orthonormal basis类
*/
#pragma once
#ifndef ONB_H
#define ONB_H

#include "utilities.h"

class onb {
public:
    onb() {}

    inline vec3 operator[](int i) const { return axis[i]; }

    vec3 u() const { return axis[0]; }
    vec3 v() const { return axis[1]; }
    vec3 w() const { return axis[2]; }

    vec3 local(double a, double b, double c) const {
        return a * u() + b * v() + c * w();
    }

    vec3 local(const vec3& a) const {
        return a.x() * u() + a.y() * v() + a.z() * w();
    }

    void build_from_w(const vec3&);

public:
    vec3 axis[3];
};


void onb::build_from_w(const vec3& n) {
    axis[2] = normalize(n);
    vec3 a = (fabs(w().x()) > 0.9) ? vec3(0, 1, 0) : vec3(1, 0, 0);
    axis[1] = normalize(cross(w(), a));
    axis[0] = cross(w(), v());
}

#endif

现在我们可以修改 lambertian 材质的散射函数：

// lambertian材质类，在单位球面上采样得到散射方向
class lambertian : public material {
public:
    lambertian(const color& a) : albedo(make_shared<solid_color>(a)) {}
    lambertian(shared_ptr<texture> a) : albedo(a) {}

    virtual bool scatter(
        ray& r_in, const hit_record& rec, color& attenuation, ray& scattered, double& pdf
    ) const override {
        // 构建法线空间的标准正交基
        onb uvw;
        uvw.build_from_w(rec.normal);
        // 得到法线空间下概率分布为cos(theta)/pi的随机方向
        auto direction = uvw.local(random_cosine_direction());
        scattered = ray(rec.p, normalize(direction), r_in.time());
        attenuation = albedo->value(rec.u, rec.v, rec.p);
        // 采样光线的概率密度，即cos(theta)/pi
        pdf = dot(uvw.w(), scattered.direction()) / pi;
        return true;
    }
    // 散射光线的概率密度
    double scattering_pdf(
        const ray& r_in, const hit_record& rec, const ray& scattered
    ) const {
        auto cosine = dot(rec.normal, normalize(scattered.direction()));
        return cosine < 0 ? 0 : cosine / pi;
    }

public:
    shared_ptr<texture> albedo;   //反射率
};

得到的效果：

到目前为止我们实际上没有对之前的实现有什么实质性的更改，只是换了一种实现方式，所以得到的效果自然也是差不多的。但是改变实现方式是为了能够实现重要性采样，下一节我们将直接对光源进行采样。