【RayTracer】（十八）重要性采样

到目前为止我们已经实现了一个完整的光线追踪器，但距离真正的光线追踪其还差极为艰难的一步，也就是我们之前在渲染 Cornell Box 的时候提到的，画面噪声很大是因为光源太小，由于我们对散射光线的随机采样是使用最基本的采样方式，所以当光源很小的时候，光线打到光源的概率就很小，也就导致了噪声过大。从这一节开始我们就来解决这个问题。

1 再谈渲染方程

首先我们来回顾图形学中学过的渲染方程：

实际上在前面的光线追踪器中我们已经实现了这个渲染方程，但是只实现了一个特殊情况，现在我们来深入分析一下我们是如何实现的。

我们是在 ray_color 函数中实现这个渲染方程的，渲染方程中的入射光线和出射光线的强度在我们的代码中其实就是 ray_color 函数计算的颜色。

ray_color 函数的r_in 参数最开始传入的是我们从像素中投射出的视线，也就是观察方向，我们根据观察方向通过材质的散射函数随机采样出一条对于我们来说真正的入射光线，然后递归的计算这个入射光线的颜色，并返回 albedo * ray_color，其中反射率 albedo 就是出射光线和入射光线的比值，乘以入射光线颜色，自然就得到了出射光线的颜色，也就是我们最终观察到的颜色。整个过程不断递归，每次传入 ray_color 函数的入射光线实际上是上一次计算的入射光线，是本次计算的出射光线。

但是我们发现在 ray_color 函数中并没有体现出 BRDF 的存在。这是由于我们实现的是一个特殊情况。

首先我们对渲染方程中的 BRDF 项做一些变形。我们知道 BRDF 可以表示为：

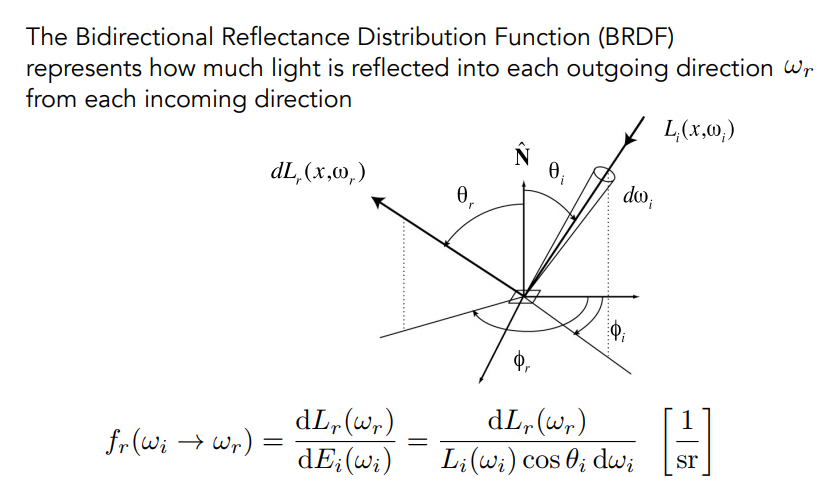
从公式上看，BRDF 计算的是从每个散射方向 $\omega_r$ 出射的光的能量，和从每个入射方向 $\omega_i$ 上入射的光被着色点吸收的全部能量（在法线方向上投影的能量）的比值。双向反射分布函数的意义在于既描述了光线能量的反射比率，也描述了光线散射方向的分布。

如果一个材质会发生散射，那么就会存在一个散射光线的分布，这个分布是关于方向的，我们称之为散射光线的概率密度函数 $s(direction)$，根据上面的 BRDF 公式，我们可以把 BRDF 改写为：
$$
BRDF = \frac{albedo·s(direction)}{cos\theta}
$$
其中反射率是出射光线和入射光线的比值，描述光线的能量反射比率，散射光线的概率密度函数描述了光线散射方向的概率分布，这和上面的 BRDF 表达式是一致的。

接下来将这个 BRDF 表达式带入渲染方程中，其中夹角余弦可以写成表面法线和入射光线的点乘。于是我们可以得到：
$$
color_{out} = color_{emit} + \int_{\Omega^+}albedo·s(direction)·color_{in}
$$
这和我们代码中的：

// 得到光线颜色
color ray_color(ray& r, const color& background, const hittable& world, int depth, double RR) {
    ...

    return emitted + attenuation * ray_color(scattered, background, world, depth - 1, RR);
}

是一致的，只是代码中缺少了散射光线的概率密度函数 $s(direction)$。这是为什么呢？

在我们实现的材质中，以漫反射 lambertian 材质为例，它的计算散射方向的方法是：使用表面法线偏移着色点 p 作为单位球的球心，在该单位球面上均匀采样一点并连接该点和点 p ，形成的向量即为散射方向。这样计算出的散射方向并不是在以点 p 为球心的半球上均匀分布的，所以概率密度并不是的 $\frac{1}{2\pi}$，而是与散射光线和法线的夹角余弦 $cos\theta$ 成正比的，我们可以推导出这个概率密度函数。

为什么概率密度和 $cos\theta$ 成正比？

可以这样理解，首先概率密度函数的积分是概率，对于 cos 函数，从 0 到 $\pi/4$ 的积分和从 $\pi/4$ 到 $\pi/2$ 的积分显然是不同的，这说明我们取到的散射方向和法线的夹角在 0 到 $\pi/4$ 的概率比在 $\pi/4$ 到 $\pi/2$ 的概率更大。

在我们的代码中， lambertian 材质的散射光线方向是法线方向加上一个单位球面上随机生成的方向，也就是说，最终得到的散射光线方向是两个向量的和。如果单位球面上随机生成的方向和法线的夹角刚好是 45 度，那么他和法线的和向量与法线的夹角一定小于 45 度，如果想要和向量的夹角为 45 度，那么随机生成的向量夹角就要大于 45 度。这说明我们在一个单位球面上均匀的取随机点作为一个向量与法线相加得到散射方向，大部分的点得到的散射方向会在 0 到 $\pi/4$ 范围内，只有一小部分才会使最终的散射方向在 $\pi/4$ 到 $\pi/2$ 范围内，因此也就对应了不均匀的概率。

接下来我们推导这个概率密度函数是什么。首先我们知道，方向表示为单位立体角 $d\omega$，单位立体角是球面上的一块面积 $dA$ 和半径平方的比值，在图形学中我们推导过：
$$
d\omega = \frac{dA}{r^2} = \frac{r^2sin\theta \ d\theta \ d\phi}{r^2} = sin\theta \ d\theta \ d\phi
$$
于是对于半球面上的均匀采样，有：
$$
\int_0^{2\pi}\int_0^{\pi/2}pdf·sin\theta \ d\theta \ d\phi = 1
$$
而单位半球面的积分就是半球的表面积 $2\pi$，于是半球面上的均匀分布就是：
$$
pdf(x) = \frac{1}{2\pi}
$$
同理，我们现在要求的概率密度函数和 $cos\theta$ 成正比，于是可以表示为：
$$
pdf(x) = C·cos\theta
$$
带入上面的积分有：
$$
\int_0^{2\pi}\int_0^{\pi/2}C·cos\theta·sin\theta \ d\theta \ d\phi = 1
$$
半球面上对 $cos\theta$ 积分结果为 $\pi$，因此：
$$
C·\pi = 1
$$
于是可以得到我们实现的 lambertian 材质的散射光线的概率密度函数为：
$$
s(direction) = \frac{cos\theta}{\pi}
$$
接下来继续回顾图形学中的知识，我们求解渲染方程使用的是蒙特卡洛积分的方法，也就是按照某个概率分布 $p(x)$ 对被积变量进行随机采样，于是原积分可以通过如下方式计算：
$$
F_N = \frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)},\ X_i \sim p(x)
$$
那么现在的渲染方程就可以通过蒙特卡洛积分计算：
$$
color_{out} = color_{emit} + \sum \frac{albedo·s(direction)·color_{in}}{p(direction)}
$$
如果我们选择对光线随机采样的概率密度和散射光线本身的概率密度分布一致，即：
$$
p(direction) = s(direction) = \frac{cos\theta}{\pi}
$$
显然渲染方程变为：
$$
color_{out} = color_{emit} + \sum albedo·color_{in}
$$
也就是我们现在代码中的：

// 得到光线颜色
color ray_color(ray& r, const color& background, const hittable& world, int depth, double RR) {
    ...

    return emitted + attenuation * ray_color(scattered, background, world, depth - 1, RR) / RR;
}

也就是说，在我们之前的实现中，隐式的把对光线随机采样的概率密度设置为了永远和散射光线的概率密度一样，无论是漫反射材质还是金属材质又或者是其他材质，我们不关注他们散射光线的概率密度什么，反正我们采样的概率密度和它们一致，所以渲染方程永远可以表示为上面那样。

那么这样做为什么可以得到正确的结果呢？之前我们在图形学中也提到过，随机采样的概率分布越接近该变量原本的概率分布，蒙特卡洛积分收敛的也就越好，这会在之后展开讨论。

现在为了实现更一般的渲染方程，我们需要改写现在的代码。

首先修改材质抽象类，为散射光线的计算加入采样光线的 pdf：

class material {
public:
    virtual bool scatter(
        ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
    ) const {
        return false;
    };
    // 带有采样pdf的散射函数
    virtual bool scatter(
        ray& r_in, const hit_record& rec, color& albedo, ray& scattered, double& pdf
    ) const {
        return false;
    };
    // 计算材质散射光线的pdf
    virtual double scattering_pdf(
        const ray& r_in, const hit_record& rec, const ray& scattered
    ) const {
        return 0;
    }
    virtual color emitted(double u, double v, const point3& p) const {
        return color(0, 0, 0);
    }
};

然后修改 lambertian 材质的散射函数：

// lambertian材质类，在单位球面上采样得到散射方向
class lambertian : public material {
public:
    lambertian(const color& a) : albedo(make_shared<solid_color>(a)) {}
    lambertian(shared_ptr<texture> a) : albedo(a) {}

    virtual bool scatter(
        ray& r_in, const hit_record& rec, color& attenuation, ray& scattered, double& pdf
    ) const override {
        // 这里省略了rec.p + rec.normal + random_unit_vector() - rec.p中的rec.p;
        auto scatter_direction = rec.normal + random_unit_vector();
        // 如果散射方向为0，则取法线方向作为散射方向
        if (scatter_direction.near_zero())
        {
            scatter_direction = rec.normal;
        }
        // 散射光线时刻和入射光线一样
        scattered = ray(rec.p, normalize(scatter_direction), r_in.time());
        attenuation = albedo->value(rec.u, rec.v, rec.p);
        // 采样光线的概率密度
        pdf = dot(rec.normal, scattered.direction()) / pi;
        return true;
    }
    // 散射光线的概率密度
    double scattering_pdf(
        const ray& r_in, const hit_record& rec, const ray& scattered
    ) const {
        auto cosine = dot(rec.normal, normalize(scattered.direction()));
        return cosine < 0 ? 0 : cosine / pi;
    }

public:
    shared_ptr<texture> albedo;   //反射率
};

最后修改 ray_color 函数：

// 得到光线颜色
color ray_color(ray& r, const color& background, const hittable& world, int depth, double RR) {
    hit_record rec;

    // 光线弹射指定次数后开始用RR算法终止递归
    if (depth < 0 && random_double() >= RR) return color(0, 0, 0);
    
    // 如果光线没有打到任何物体，返回背景颜色
    // 这里的t的下界设为0.001是为了防止一些光线弹射到物体上得到的t非常接近0，比如可能出现0.000001这样的值
    if (!world.hit(r, 0.001, infinity, rec))
        return background;
        
    // 根据物体材质得到光线传播方向、反射率及自发光颜色
    ray scattered;
    color albedo;
    color emitted = rec.mat_ptr->emitted(rec.u, rec.v, rec.p);
    // 采样光线的概率密度
    double pdf;

    // 对于光源，不会发生散射，返回光源颜色
    if (!rec.mat_ptr->scatter(r, rec, albedo, scattered, pdf))
        return emitted;

    // 渲染方程
    return emitted
        + albedo * rec.mat_ptr->scattering_pdf(r, rec, scattered)
        * ray_color(scattered, background, world, depth - 1, RR) / pdf / RR;
}

可以得到和之前一样的效果：

如果我们把采样光线改为在半球上均匀采样，此时采样光线的 pdf 就是 $\frac{1}{2\pi}$ ，于是我们只要修改：

virtual bool scatter(
        ray& r_in, const hit_record& rec, color& attenuation, ray& scattered, double& pdf
    ) const override {
        //auto scatter_direction = rec.normal + random_unit_vector();
        // 改为半球均匀采样 
        auto scatter_direction = random_in_hemisphere(rec.normal);
        if (scatter_direction.near_zero())
        {
            scatter_direction = rec.normal;
        }
        scattered = ray(rec.p, normalize(scatter_direction), r_in.time());
        attenuation = albedo->value(rec.u, rec.v, rec.p);
        // 采样光线的概率密度
        //pdf = dot(rec.normal, scattered.direction()) / pi;
        pdf = 0.5 / pi;
        return true;
    }

得到的效果：

使用什么样的采样 pdf 完全取决于我们的选择，但是使用什么样的 pdf 效果好刚才已经给出了答案，随机采样的 pdf 形状越接近函数原本的形状，蒙特卡洛估计收敛的效果就会越好。下面我们来推导这是为什么。

2 重要性采样

要了解重要性采样的原理就要先深入理解蒙特卡洛积分，首先我们来分析为什么蒙特卡洛积分可以得到原积分的估计值。根据蒙特卡洛积分的计算方法：
$$
F_N = \frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)},\ X_i \sim p(x)
$$
首先我们把积分变量看做了一个随机变量 X，然后构造了一个随机采样的分布 p(X)，利用这个分布我们可以构造一个新的随机变量：
$$
Y = \frac{f(X)}{p(X)}
$$
概率论告诉我们的如果一个随机变量 X 的期望是 E(X)，那么随机变量 f(X) 的期望就是 E(f(X))，于是蒙特卡洛积分 $F_N$ 的期望就是：
$$
E[F_N] = E[\frac{1}{N}\sum_{i=1}^N\frac{f(X_i)}{p(X_i)}]
$$
也就是：
$$
E[F_N] = \frac{1}{N} \sum_{i=1}^NE[Y_i]
$$
连续型随机变量的期望就是对概率密度函数的积分，所以：
$$
E[Y_i] = \int_a^b \frac{f(x)}{p(x)}p(x)dx = \int_a^b{f(x)}dx
$$
带入上式得：
$$
E[F_N] = \frac{1}{N} \sum_{i=1}^N\int_a^b{f(x)}dx = \int_a^b{f(x)}dx
$$
以上证明过程表明，若我们根据公式来构造一个新的随机变量 $F_N$ ，则 $F_N$ 的期望就是原积分的结果，随着 N 的增加，$F_N$ 就越逼近理论上的积分值，即蒙特卡洛积分是原积分的一个无偏估计。

接下来我们看蒙特卡洛估计的方差：
$$
\sigma^2[F_N] = \sigma^2[\frac{1}{N}\sum_{i=1}^N\frac{f(X_i)}{p(X_i)}]
$$
即：
$$
\sigma^2[F_N] = \frac{1}{N^2}\sum_{i=1}^N\sigma^2[Y_i]
$$
于是可以得到：
$$
\sigma^2[F_N] = \frac{1}{N^2}N\sigma^2[Y]=\frac{1}{N}\sigma^2[Y]
$$
所以蒙特卡洛积分的标准差就是：
$$
\sigma[F_N] = \frac{1}{\sqrt{n}}\sigma[Y]
$$
这个结果告诉我们，估计值的不稳定来源于随机变量 Y 的取值不稳定。换句话说，如果随机变量：
$$
Y_i = \frac{f(X_i)}{p(X_i)}
$$
因不同 $X_i$ 的取值变化地越剧烈，就会造成 Y 的方差较大，也就导致估计值的收敛速度越慢。这证明了，如果 p(x) 的形状越接近 f(x)，则有益于最终结果的收敛。

上述思想就是“重要性采样”的方法，即对积分值有重要贡献，即 f(x) 较大的被积函数区间，我们以较大概率生成处于这个区间附近的随机变量，就可以快速逼近理论值。

应用到光线追踪中，光源方向的光线对最终渲染方程积分结果的贡献更大，如果使用我们现在的均匀随机采样，由于光源很小，得到光源方向的光线的概率就很小，自然对最终结果的估计就会产生较大的偏差，体现在画面上就是有很大的噪声。于是为了消除噪声，我们应该使用重要性采样，生成更多光源方向的光线。

当然，如果我们采样更多的随机光线到光源，会导致积分结果过大，也就是画面过亮，而产生不正确的效果，因此我们需要降低这些样本的权重，在蒙特卡洛积分的公式中，除以概率密度函数就是为了解决这个问题，概率密度大的样本取到的相对概率大，除以这个概率可以削弱该样本的权重，以抵消这种不均衡。