LycTechStack

Lyc的个人成长技术栈

0%

【RayTracer】（十五）立方体和变换

发表于 更新于 分类于
本文字数： 7.3k 阅读时长 ≈ 7 分钟

上一节中我们实现了光源和矩形物体，并初步创建了一个 Cornell Box 场景，但场景中还缺少两个立方体，并且立方体和墙面之间存在一定的旋转角度，因此这一节我们需要实现一个立方体物体类，并且支持旋转和平移。

1 轴对齐立方体

先使用轴对齐矩形实现一个轴对齐立方体类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#pragma once
#ifndef BOX_H
#define BOX_H

#include "utilities.h"
#include "aarect.h"
#include "hittable_list.h"

class box : public hittable {
public:
    box() {}
    box(const point3& p0, const point3& p1, shared_ptr<material> ptr);

    virtual bool hit(ray& r, double t_min, double t_max, hit_record& rec) const override;

    virtual bool bounding_box(double time0, double time1, aabb& output_box) const override {
        output_box = aabb(box_min, box_max);
        return true;
    }

public:
    point3 box_min;
    point3 box_max;
    hittable_list sides;
};

box::box(const point3& p0, const point3& p1, shared_ptr<material> ptr) {
    box_min = p0;
    box_max = p1;

    sides.add(make_shared<xy_rect>(p0.x(), p1.x(), p0.y(), p1.y(), p1.z(), ptr));
    sides.add(make_shared<xy_rect>(p0.x(), p1.x(), p0.y(), p1.y(), p0.z(), ptr));

    sides.add(make_shared<xz_rect>(p0.x(), p1.x(), p0.z(), p1.z(), p1.y(), ptr));
    sides.add(make_shared<xz_rect>(p0.x(), p1.x(), p0.z(), p1.z(), p0.y(), ptr));

    sides.add(make_shared<yz_rect>(p0.y(), p1.y(), p0.z(), p1.z(), p1.x(), ptr));
    sides.add(make_shared<yz_rect>(p0.y(), p1.y(), p0.z(), p1.z(), p0.x(), ptr));
}

bool box::hit(ray& r, double t_min, double t_max, hit_record& rec) const {
    return sides.hit(r, t_min, t_max, rec);
}

#endif

然后将 box 添加到 Cornell Box 场景中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// Cornell Box场景
hittable_list cornell_box() {
    hittable_list objects;

    auto red = make_shared<lambertian>(color(.65, .05, .05));
    auto white = make_shared<lambertian>(color(.73, .73, .73));
    auto green = make_shared<lambertian>(color(.12, .45, .15));
    auto light = make_shared<diffuse_light>(color(15, 15, 15));

    objects.add(make_shared<yz_rect>(0, 555, 0, 555, 555, green));
    objects.add(make_shared<yz_rect>(0, 555, 0, 555, 0, red));
    objects.add(make_shared<xz_rect>(213, 343, 227, 332, 554, light));
    objects.add(make_shared<xz_rect>(0, 555, 0, 555, 0, white));
    objects.add(make_shared<xz_rect>(0, 555, 0, 555, 555, white));
    objects.add(make_shared<xy_rect>(0, 555, 0, 555, 555, white));

    objects.add(make_shared<box>(point3(130, 0, 65), point3(295, 165, 230), white));
    objects.add(make_shared<box>(point3(265, 0, 295), point3(430, 330, 460), white));

    return objects;
}

得到的效果：

CornellBoxComplete

2 Instances

接下来我们要实现立方体的旋转，更一般地，我们不止要让立方体旋转，而是要让场景中的所有物体都能够运动，运动包括平移和旋转。在光线追踪器中，这些都是通过 Instances 来实现的，Instances 可以认为是一个几何变换器，可以将传入的物体按照给定的参数和方式进行变换，因此我们要实现这些几何变换的 Instances 类。

2.1 平移

首先是平移变换类，在光线追踪器中实现物体平移不是通过真的把物体移动到某个位置，因为物体一旦被放入场景再去变换位置就需要费很大的功夫，所以实现物体平移是通过向反方向移动光线来实现的，比如：

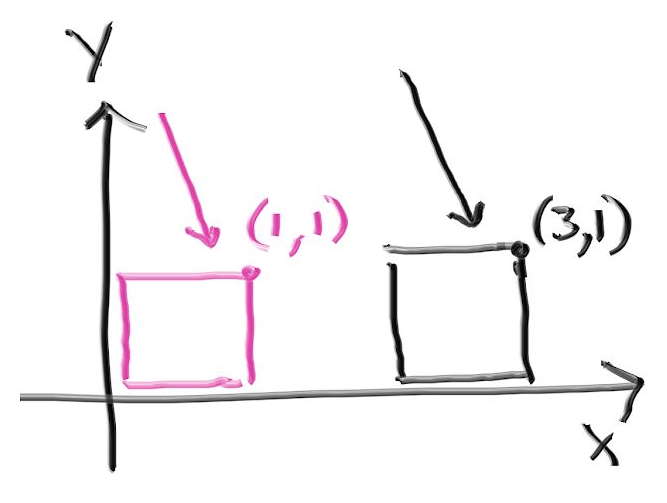
fig-2.06-ray-box

要把粉色的正方形沿 x 轴向右移动两个单位，我们可以通过把光线沿 x 轴向左移动两个单位来实现。

注意和之前实现的移动的球体做区分，这里的移动不是在一段时间内的运动，而是改变场景中物体的摆放方式。

平移变换类的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// 平移变换
class translate : public hittable {
public:
    translate(shared_ptr<hittable> p, const vec3& displacement)
        : ptr(p), offset(displacement) {}

    virtual bool hit(
        ray& r, double t_min, double t_max, hit_record& rec) const override;

    virtual bool bounding_box(double time0, double time1, aabb& output_box) const override;

public:
    shared_ptr<hittable> ptr;
    vec3 offset;
};

bool translate::hit(ray& r, double t_min, double t_max, hit_record& rec) const {
    // 光线向反方向平移
    ray moved_r(r.origin() - offset, r.direction(), r.time());
    
    // 计算交点，这里计算出的交点是相对坐标，物体还在原本的地方
    if (!ptr->hit(moved_r, t_min, t_max, rec))
        return false;

    // 把物体和光线的交点加上偏移，得到平移后的物体和光线的交点在世界空间的绝对坐标
    // 这才相当于把物体移动了
    rec.p += offset;
    rec.set_face_normal(moved_r, rec.normal);

    return true;
}

bool translate::bounding_box(double time0, double time1, aabb& output_box) const {
    if (!ptr->bounding_box(time0, time1, output_box))
        return false;

    output_box = aabb(
        output_box.min() + offset,
        output_box.max() + offset);

    return true;
}

2.2 旋转

旋转的思路和平移一样，也是先反方向旋转光线，得到交点后对交点再进行正向旋转，不同的是旋转后交点法线也要相应变换，在 Shader 学习中我们知道对法线变换要用变换矩阵的逆转置矩阵，旋转矩阵是正交矩阵，逆转置矩阵就是其本身。

绕 y 轴旋转的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
// 绕y轴旋转
class rotate_y : public hittable {
public:
    rotate_y(shared_ptr<hittable> p, double angle);

    virtual bool hit(
        ray& r, double t_min, double t_max, hit_record& rec) const override;

    virtual bool bounding_box(double time0, double time1, aabb& output_box) const override {
        output_box = bbox;
        return hasbox;
    }

public:
    shared_ptr<hittable> ptr;
    double sin_theta;
    double cos_theta;
    bool hasbox;
    aabb bbox;
};

// 构造函数，计算旋转后的bounding box及其他的基本成员
rotate_y::rotate_y(shared_ptr<hittable> p, double angle) : ptr(p) {
    auto radians = degrees_to_radians(angle);
    sin_theta = sin(radians);
    cos_theta = cos(radians);
    hasbox = ptr->bounding_box(0, 1, bbox);

    point3 min(infinity, infinity, infinity);
    point3 max(-infinity, -infinity, -infinity);

    // 遍历bounding box的每个顶点，并进行变换
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            for (int k = 0; k < 2; k++) {
                auto x = i * bbox.max().x() + (1 - i) * bbox.min().x();
                auto y = j * bbox.max().y() + (1 - j) * bbox.min().y();
                auto z = k * bbox.max().z() + (1 - k) * bbox.min().z();

                auto newx = cos_theta * x + sin_theta * z;
                auto newz = -sin_theta * x + cos_theta * z;

                vec3 tester(newx, y, newz);

                for (int c = 0; c < 3; c++) {
                    min[c] = fmin(min[c], tester[c]);
                    max[c] = fmax(max[c], tester[c]);
                }
            }
        }
    }

    bbox = aabb(min, max);
}

bool rotate_y::hit(ray& r, double t_min, double t_max, hit_record& rec) const {
    auto origin = r.origin();
    auto direction = r.direction();

    // 光线向反方向旋转
    origin[0] = cos_theta * r.origin()[0] - sin_theta * r.origin()[2];
    origin[2] = sin_theta * r.origin()[0] + cos_theta * r.origin()[2];
    // 因为光线方向实际上是两个点的差，所以也可以直接应用变换矩阵
    direction[0] = cos_theta * r.direction()[0] - sin_theta * r.direction()[2];
    direction[2] = sin_theta * r.direction()[0] + cos_theta * r.direction()[2];

    ray rotated_r(origin, direction, r.time());

    // 得到的交点同样是相对的坐标
    if (!ptr->hit(rotated_r, t_min, t_max, rec))
        return false;

    auto p = rec.p;
    auto normal = rec.normal;

    // 将交点进行旋转
    p[0] = cos_theta * rec.p[0] + sin_theta * rec.p[2];
    p[2] = -sin_theta * rec.p[0] + cos_theta * rec.p[2];
    // 法线也要旋转，法线变换应该用原变换矩阵的逆转置矩阵，旋转矩阵正交因此逆转置矩阵就是原矩阵
    normal[0] = cos_theta * rec.normal[0] + sin_theta * rec.normal[2];
    normal[2] = -sin_theta * rec.normal[0] + cos_theta * rec.normal[2];

    rec.p = p;
    rec.set_face_normal(rotated_r, normal);

    return true;
}

3 完整的 Cornell Box

利用实现的立方体和几何变换类，来得到完整的 Cornell Box 场景：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// Cornell Box场景
hittable_list cornell_box() {
    hittable_list objects;

    auto red = make_shared<lambertian>(color(.65, .05, .05));
    auto white = make_shared<lambertian>(color(.73, .73, .73));
    auto green = make_shared<lambertian>(color(.12, .45, .15));
    auto light = make_shared<diffuse_light>(color(15, 15, 15));

    objects.add(make_shared<yz_rect>(0, 555, 0, 555, 555, green));
    objects.add(make_shared<yz_rect>(0, 555, 0, 555, 0, red));
    objects.add(make_shared<xz_rect>(213, 343, 227, 332, 554, light));
    objects.add(make_shared<xz_rect>(0, 555, 0, 555, 0, white));
    objects.add(make_shared<xz_rect>(0, 555, 0, 555, 555, white));
    objects.add(make_shared<xy_rect>(0, 555, 0, 555, 555, white));

    shared_ptr<hittable> box1 = make_shared<box>(point3(0, 0, 0), point3(165, 330, 165), white);
    box1 = make_shared<rotate_y>(box1, 15);
    box1 = make_shared<translate>(box1, vec3(265, 0, 295));
    objects.add(box1);

    shared_ptr<hittable> box2 = make_shared<box>(point3(0, 0, 0), point3(165, 165, 165), white);
    box2 = make_shared<rotate_y>(box2, -18);
    box2 = make_shared<translate>(box2, vec3(130, 0, 65));
    objects.add(box2);

    return objects;
}

效果如下：

CornellBoxFinal

---- 本文结束 知识又增加了亿点点！----

文章版权声明 1、博客名称：LycTechStack
2、博客网址：https://lz328.github.io/LycTechStack.github.io/
3、本博客的文章部分内容可能来源于网络，仅供大家学习与参考，如有侵权，请联系博主进行删除处理。
4、本博客所有文章版权归博主所有，如需转载请标明出处。
相关文章