【RayTracer】（十四）光源

之前的场景中一直缺少一个重要的元素，那就是光源，这一节我们来实现光源，这样我们之后就可以随意控制场景中的光照了。

1 自发光材质

光源可以认为是会自发光的材质，并且其他光线到达其表面也不会发生散射，这样的材质实现非常简单：

// 自发光材质
class diffuse_light : public material {
public:
    diffuse_light(shared_ptr<texture> a) : emit(a) {}
    diffuse_light(color c) : emit(make_shared<solid_color>(c)) {}

    virtual bool scatter(
        const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
    ) const override {
        return false;
    }

    virtual color emitted(double u, double v, const point3& p) const override {
        return emit->value(u, v, p);
    }

public:
    shared_ptr<texture> emit;
};

注意到上面还重载了另一个虚函数 emitted，因此要在 material 抽象类中加入 emitted 的声明，但因为我们不需要所有派生类都实现这个方法，因此不必定义为纯虚函数：

class material {
public:
    // 纯虚函数，产生散射光线并给定光线衰减系数
    virtual bool scatter(
        ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
    ) const = 0;
    // 自发光虚函数，不必所有派生类都进行实现
    virtual color emitted(double u, double v, const point3& p) const {
        return color(0, 0, 0);
    }
};

2 为场景添加背景颜色

为了之后测试光源，我们需要一个全黑的背景，这样所有的光线就都来自于光源了，为此我们在 ray_color 函数中增加一个背景颜色的参数，并作相应的修改：

// 得到光线颜色
color ray_color(ray& r, const color& background, const hittable& world, int depth, double RR) {
	hit_record rec;

	// 光线弹射指定次数后开始用RR算法终止递归
	if (depth < 0 && random_double() >= RR) return color(0, 0, 0);
	
	// 如果光线没有打到任何物体，返回背景颜色
	// 这里的t的下界设为0.001是为了防止一些光线弹射到物体上得到的t非常接近0，比如可能出现0.000001这样的值
	if (!world.hit(r, 0.001, infinity, rec))
		return background;
		
	// 根据物体材质得到光线传播方向、反射率及自发光颜色
	ray scattered;
	color attenuation;
	color emitted = rec.mat_ptr->emitted(rec.u, rec.v, rec.p);
	// 对于光源，不会发生散射，返回光源颜色
	if (!rec.mat_ptr->scatter(r, rec, attenuation, scattered))
		return emitted;

	return emitted + attenuation * ray_color(scattered, background, world, depth - 1, RR) / RR;
}

然后在主函数中增加背景颜色：

...
    
/*******创建场景*******/
hittable_list world;

point3 lookfrom;
point3 lookat;
auto vfov = 40.0;
auto aperture = 0.0;
color background(0, 0, 0);

int sence = 1;
switch (sence) {
    case 1:
        ...
        background = color(0.70, 0.80, 1.00);
        ...
        break;
    case 2:
        ...
        background = color(0.70, 0.80, 1.00);
        ...
        break;
    case 3:
        ...
        background = color(0.70, 0.80, 1.00);
        ...
        break;
    case 4:
        ...
        background = color(0.70, 0.80, 1.00);
        ...
        break;
    default:
    case 5:
        background = color(0.0, 0.0, 0.0);
        break;
}

...
    
    pixel_color += ray_color(r, background, world, min_bounce, RR);

...

为了方便，我们把之前的场景的背景统一设置为了天空的蓝白色。

3 矩形物体

接下来我们实现另一类物体——矩形，矩形在我们之后的场景中非常重要，它既可以作为面光源，也可以组合成立方体等等。为了实现矩形物体类，我们首先要考虑的就是它的 hit 函数，这里为了实现方便，我们实现的矩形是一个轴对齐矩形。

对于一个三维空间中存在于 xy 平面内的矩形，可以直接用它的 z 坐标来描述它的位置，比如 z = k，又因为它是轴对齐矩形，因此可以用四条线 x = x0, x = x1, y = y0, y = y1 来定义这个矩形，这和之前的轴对齐包围盒非常相似，如下图：

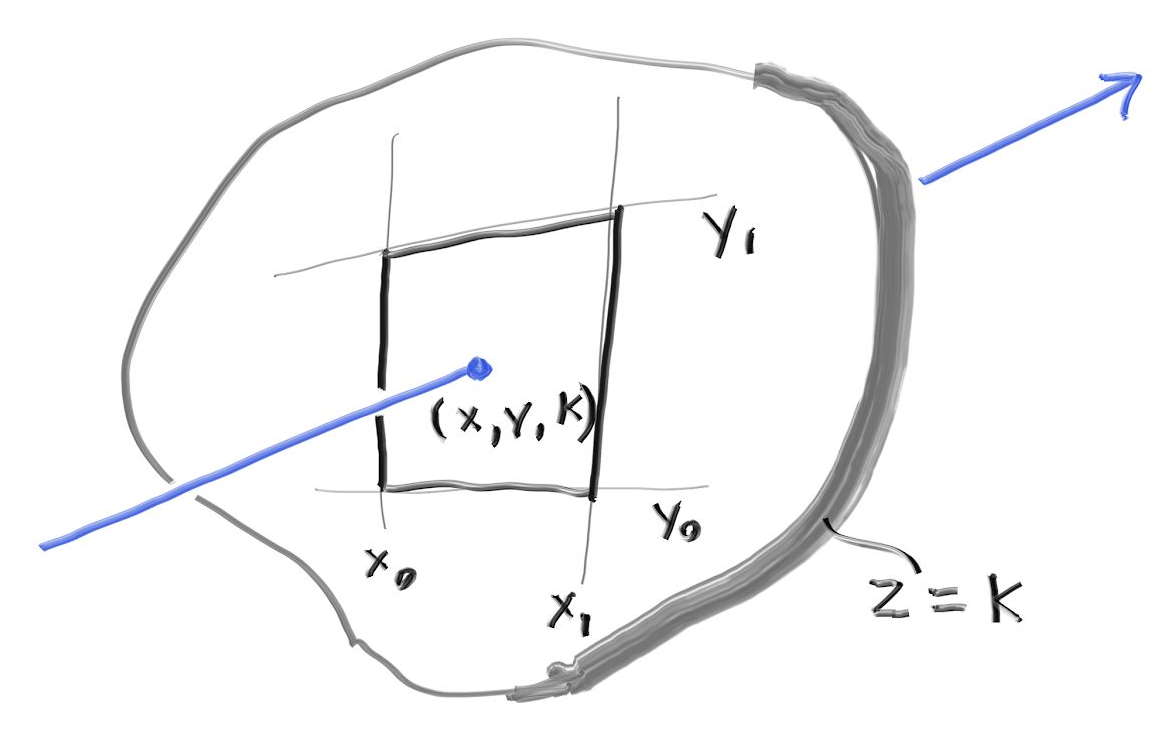
于是求光线和矩形的交点可以类似于图形学中求光线和三角形的交点，分为两步，先求光线和 z = k 平面的交点，然后判断该交点是否在矩形内部。光线和 z = k 平面的交点非常容易求得，对于光线 $P(t) = A + tb$，可以直接用它的 z 坐标和 z = k 联立：
$$
P_z(t) = A_z + tb_z = k
$$
于是可以求得与 z = k 平面相交的 t：
$$
t = \frac{k-A_z}{b_z}
$$
然后将该 t 带入光线的其他两个维度的坐标方程就可以得到 x 和 y 的坐标：
$$
x = A_x + tb_x,\ y = A_y+tb_y
$$
如果光线和矩形有交点，那么必须满足：
$$
x_0 < x < x_1 \ 且\ y_0 < y < y_1
$$
有了 hit 函数，接下来考虑一个矩形物体的包围盒，由于我们的轴对齐矩形是没有 z 方向的厚度的，这在 BVH 随机维度划分的时候会出问题，因此我们为矩形物体包围盒的 z 方向填充一个很小的长度。

一个 xy 平面的轴对齐矩形物体类的实现如下：

/*
* 轴对齐矩形类aarect
*/
#pragma once
#ifndef AARECT_H
#define AARECT_H

#include "utilities.h"
#include "hittable.h"

class xy_rect : public hittable {
public:
    xy_rect() {}

    xy_rect(double _x0, double _x1, double _y0, double _y1, double _k,
        shared_ptr<material> mat)
        : x0(_x0), x1(_x1), y0(_y0), y1(_y1), k(_k), mp(mat) {};

    virtual bool hit(ray& r, double t_min, double t_max, hit_record& rec) const override;

    virtual bool bounding_box(double time0, double time1, aabb& output_box) const override {
        // z 方向填充一个很小的长度，防止 BVH 划分出问题
        output_box = aabb(point3(x0, y0, k - 0.0001), point3(x1, y1, k + 0.0001));
        return true;
    }

public:
    shared_ptr<material> mp;
    double x0, x1, y0, y1, k;
};

bool xy_rect::hit(ray& r, double t_min, double t_max, hit_record& rec) const {
    auto t = (k - r.origin().z()) / r.direction().z();
    if (t < t_min || t > t_max)
        return false;
    auto x = r.origin().x() + t * r.direction().x();
    auto y = r.origin().y() + t * r.direction().y();
    if (x < x0 || x > x1 || y < y0 || y > y1)
        return false;
    rec.u = (x - x0) / (x1 - x0);
    rec.v = (y - y0) / (y1 - y0);
    rec.t = t;
    auto outward_normal = vec3(0, 0, 1);
    rec.set_face_normal(r, outward_normal);
    rec.mat_ptr = mp;
    rec.p = r.at(t);
    return true;
}

#endif

4 测试光源

现在我们来创建一个包含一个面光源的简单场景：

// 简单光照场景
hittable_list simple_light() {
    hittable_list objects;

    auto pertext = make_shared<noise_texture>(4);
    objects.add(make_shared<sphere>(
        point3(0, -1000, 0), point3(0, -1000, 0), 0.0, 1.0, 1000, make_shared<lambertian>(pertext)));
    objects.add(make_shared<sphere>(
        point3(0, 2, 0), point3(0, 2, 0), 0.0, 1.0, 2, make_shared<lambertian>(pertext)));

    auto difflight = make_shared<diffuse_light>(color(4, 4, 4));
    objects.add(make_shared<xy_rect>(3, 5, 1, 3, -2, difflight));

    return objects;
}

注意到我们给定的光源的颜色是大于 (1, 1, 1) 的，这是为了保证光源足够亮，以照亮其他物体。

然后修改主函数：

#include <iostream>
#include <string>
#include <omp.h>
#define STB_IMAGE_WRITE_IMPLEMENTATION
#include "stb_image_write.h"
#include "hittable_list.h"
#include "sphere.h"
#include "color.h"
#include "camera.h"
#include "sence.h"
#include "aarect.h"

...
    
int main() {
    ...
    switch (sence) {
        ...
        default:
        case 5:
            world = simple_light();
            samples_per_pixel = 400;
            background = color(0,0,0);
            lookfrom = point3(26,3,6);
            lookat = point3(0,2,0);
            vfov = 20.0;
            break;
    }
    ...

得到的效果如下：

我们也可以使用球体作为光源：

5 其他轴对齐矩形

现在我们增加其他两个平面的轴对齐矩形的实现：

// xz平面矩形
class xz_rect : public hittable {
public:
    xz_rect() {}

    xz_rect(double _x0, double _x1, double _z0, double _z1, double _k,
        shared_ptr<material> mat)
        : x0(_x0), x1(_x1), z0(_z0), z1(_z1), k(_k), mp(mat) {};

    virtual bool hit(ray& r, double t_min, double t_max, hit_record& rec) const override;

    virtual bool bounding_box(double time0, double time1, aabb& output_box) const override {
        output_box = aabb(point3(x0, k - 0.0001, z0), point3(x1, k + 0.0001, z1));
        return true;
    }

public:
    shared_ptr<material> mp;
    double x0, x1, z0, z1, k;
};

bool xz_rect::hit(ray& r, double t_min, double t_max, hit_record& rec) const {
    auto t = (k - r.origin().y()) / r.direction().y();
    if (t < t_min || t > t_max)
        return false;
    auto x = r.origin().x() + t * r.direction().x();
    auto z = r.origin().z() + t * r.direction().z();
    if (x < x0 || x > x1 || z < z0 || z > z1)
        return false;
    rec.u = (x - x0) / (x1 - x0);
    rec.v = (z - z0) / (z1 - z0);
    rec.t = t;
    auto outward_normal = vec3(0, 1, 0);
    rec.set_face_normal(r, outward_normal);
    rec.mat_ptr = mp;
    rec.p = r.at(t);
    return true;
}

// yz平面矩形
class yz_rect : public hittable {
public:
    yz_rect() {}

    yz_rect(double _y0, double _y1, double _z0, double _z1, double _k,
        shared_ptr<material> mat)
        : y0(_y0), y1(_y1), z0(_z0), z1(_z1), k(_k), mp(mat) {};

    virtual bool hit(ray& r, double t_min, double t_max, hit_record& rec) const override;

    virtual bool bounding_box(double time0, double time1, aabb& output_box) const override {
        output_box = aabb(point3(k - 0.0001, y0, z0), point3(k + 0.0001, y1, z1));
        return true;
    }

public:
    shared_ptr<material> mp;
    double y0, y1, z0, z1, k;
};

bool yz_rect::hit(ray& r, double t_min, double t_max, hit_record& rec) const {
    auto t = (k - r.origin().x()) / r.direction().x();
    if (t < t_min || t > t_max)
        return false;
    auto y = r.origin().y() + t * r.direction().y();
    auto z = r.origin().z() + t * r.direction().z();
    if (y < y0 || y > y1 || z < z0 || z > z1)
        return false;
    rec.u = (y - y0) / (y1 - y0);
    rec.v = (z - z0) / (z1 - z0);
    rec.t = t;
    auto outward_normal = vec3(1, 0, 0);
    rec.set_face_normal(r, outward_normal);
    rec.mat_ptr = mp;
    rec.p = r.at(t);
    return true;
}

6 创建 Cornell Box

有了矩形物体，我们可以创建一个著名的 Cornell Box 场景：

// Cornell Box场景
hittable_list cornell_box() {
    hittable_list objects;

    auto red = make_shared<lambertian>(color(.65, .05, .05));
    auto white = make_shared<lambertian>(color(.73, .73, .73));
    auto green = make_shared<lambertian>(color(.12, .45, .15));
    auto light = make_shared<diffuse_light>(color(15, 15, 15));

    objects.add(make_shared<yz_rect>(0, 555, 0, 555, 555, green));
    objects.add(make_shared<yz_rect>(0, 555, 0, 555, 0, red));
    objects.add(make_shared<xz_rect>(213, 343, 227, 332, 554, light));
    objects.add(make_shared<xz_rect>(0, 555, 0, 555, 0, white));
    objects.add(make_shared<xz_rect>(0, 555, 0, 555, 555, white));
    objects.add(make_shared<xy_rect>(0, 555, 0, 555, 555, white));

    return objects;
}

修改主函数：

int main() {
    ...
    switch (0) {
        ...
        default:
        case 6:
            world = cornell_box();
            aspect_ratio = 1.0;
            image_width = 600;
            samples_per_pixel = 200;
            background = color(0,0,0);
            lookfrom = point3(278, 278, -800);
            lookat = point3(278, 278, 0);
            vfov = 40.0;
            break;
    }
    ...

得到的效果如下：

由于光源太小，导致图片中噪声非常大。