LycTechStack

Lyc的个人成长技术栈

0%

【RayTracer】（十一）纹理

发表于 分类于
本文字数： 6.9k 阅读时长 ≈ 6 分钟

我们之前实现了物体和材质，但还缺少让物体变得更丰富的纹理，因此这一节我们实现一个纹理类。纹理可以是图片，也可以是程序生成的噪声，我们之前场景中所有的物体都是纯色的，实际上纯色也可以认为是一种纹理。因此我们可以定义一个纹理抽象类，然后在此基础上实现各种不同的纹理。

1 实现纯色纹理

纯色纹理的实现非常简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#pragma once
#ifndef TEXTURE_H
#define TEXTURE_H

#include "utilities.h"

// 纹理抽象类
class texture {
public:
    virtual color value(double u, double v, const point3& p) const = 0;
};

// 纯色纹理
class solid_color : public texture {
public:
    solid_color() {}
    solid_color(color c) : color_value(c) {}

    solid_color(double red, double green, double blue)
        : solid_color(color(red, green, blue)) {}

    virtual color value(double u, double v, const vec3& p) const override {
        return color_value;
    }

private:
    color color_value;
};

#endif

接下来要更新 hit_record ，存储交点的纹理坐标：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
struct hit_record {
    point3 p;           //交点
    vec3 normal;        //交点法线
    double t;           //交点t值
    double u;           //纹理坐标
    double v;           //纹理坐标
    bool front_face;    //交点是否在物体的正面
    shared_ptr<material> mat_ptr;   //物体材质
    // 如果交点在物体的背面，则法线应该取反方向，以用于计算光照
    inline void set_face_normal(ray& r, vec3& outward_normal) {
        front_face = dot(r.direction(), outward_normal) < 0;
        normal = front_face ? outward_normal : -outward_normal;
    }
};

2 计算纹理坐标

对于球体来说，计算纹理坐标其实就是把球面上每一个点映射到纹理平面 uv 上。最简单的表示一个球面上的点的方法是用方位角 $\phi$ 和俯仰角 $\theta$，由于 uv 平面的范围是 [0, 1]，所以映射关系为：

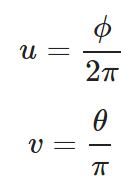
image-20220418200148322

给定方位角和俯仰角，可以计算球心在原点的单位球面上的一点：

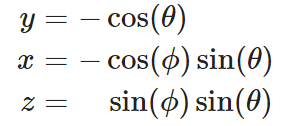
image-20220418200253256

于是我们可以通过光线和球面的交点坐标解出方位角和俯仰角然后映射为纹理坐标。根据以上公式可以看出俯仰角 $\theta = arccos(-y)$，方位角 $\phi = arctan(-z / x)$，反三角函数计算可以直接使用 <cmath> 提供的函数 acos 和 atan2：

1
2
theta = acos(-y)
phi = atan2(z, -x);

但是 atan2 返回的值的范围是 $[-\pi, \pi]$ ，并且是从 0 到 $\pi$，再从 $-\pi$ 到 0，这样映射的话，纹理坐标 u 就会是从 0 到 1/2，再从 -1/2 到 0，是不对的，但是可以利用：

1
atan2(a, b) == atan2(-a, -b) + pi;

这个公式返回的是从 0 到 $2\pi$ 的连续值，就可以映射为正确的纹理坐标了。因此可以通过：

1
2
theta = acos(-y)
phi = atan2(-z, x) + pi;

得到正确的方位角和俯仰角，然后映射得到纹理坐标。在球体类中增加：

1
2
3
4
5
6
7
8
9
10
11
12
class sphere : public hittable {
    ...
private:
    // 计算给定球面上的点p的纹理坐标，p是圆心在原点的单位球面上的坐标，一般用归一化的法线
    static void get_sphere_uv(const point3& p, double& u, double& v) {
        auto theta = acos(-p.y());
        auto phi = atan2(-p.z(), p.x()) + pi;

        u = phi / (2 * pi);
        v = theta / pi;
    }
};

同时更新球体的 hit 函数，将纹理坐标记录到 hit_record 中：

1
2
3
4
5
6
7
8
9
10
11
12
bool sphere::hit(...) {
    ...

    rec.t = root;
    rec.p = r.at(rec.t);
    vec3 outward_normal = (rec.p - center) / radius;
    rec.set_face_normal(r, outward_normal);
    get_sphere_uv(outward_normal, rec.u, rec.v);
    rec.mat_ptr = mat_ptr;

    return true;
}

3 为材质类添加纹理

现在我们可以为所有的材质增加纹理，代替之前的颜色：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// lambertian材质类，在单位球面上采样得到散射方向
class lambertian : public material {
public:
    lambertian(const color& a) : albedo(make_shared<solid_color>(a)) {}
    lambertian(shared_ptr<texture> a) : albedo(a) {}

    virtual bool scatter(
        ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
    ) const override {
        // 这里省略了rec.p + rec.normal + random_unit_vector() - rec.p中的rec.p;
        auto scatter_direction = rec.normal + random_unit_vector();
        // 如果散射方向为0，则取法线方向作为散射方向
        if (scatter_direction.near_zero())
        {
            scatter_direction = rec.normal;
        }
        // 散射光线时刻和入射光线一样
        scattered = ray(rec.p, scatter_direction, r_in.time());
        attenuation = albedo->value(rec.u, rec.v, rec.p);
        return true;
    }

public:
    shared_ptr<texture> albedo;   //反射率
};

...

4 格子纹理

我们利用两种纹理交替形成一个格子纹理，这是一种经典的生成格子纹理的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 格子纹理
class checker_texture : public texture {
public:
    checker_texture() {}

    checker_texture(shared_ptr<texture> _even, shared_ptr<texture> _odd)
        : even(_even), odd(_odd) {}

    checker_texture(color c1, color c2)
        : even(make_shared<solid_color>(c1)), odd(make_shared<solid_color>(c2)) {}

    virtual color value(double u, double v, const point3& p) const override {
        auto sines = sin(10 * p.x()) * sin(10 * p.y()) * sin(10 * p.z());
        if (sines < 0)
            return odd->value(u, v, p);
        else
            return even->value(u, v, p);
    }

public:
    shared_ptr<texture> odd;
    shared_ptr<texture> even;
};

5 测试效果

我们把随机场景中的地面的球体改为格子纹理：

1
2
3
4
5
6
7
8
9
10
hittable_list random_scene() {
    hittable_list world;

    auto checker = make_shared<checker_texture>(color(0.2, 0.3, 0.1), color(0.9, 0.9, 0.9));
    auto ground_material = make_shared<lambertian>(checker);
    world.add(make_shared<sphere>(
        point3(0, -1000, 0), point3(0, -1000, 0), 0.0, 1.0, 1000, ground_material));

    for (int a = -11; a < 11; a++) {
        ...

得到的效果：

CheckerTexture

6 新的场景

接下来我们构建一个新的场景，由于之后我们可能还会有其他场景，为了便于管理，我们新建一个 sence.h 来存放各种场景：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#pragma once

#include "hittable_list.h"
#include "sphere.h"

// 随机构建场景
hittable_list random_scene() {
    hittable_list world;

    auto checker = make_shared<checker_texture>(color(0.2, 0.3, 0.1), color(0.9, 0.9, 0.9));
    auto ground_material = make_shared<lambertian>(checker);
    world.add(make_shared<sphere>(
        point3(0, -1000, 0), point3(0, -1000, 0), 0.0, 1.0, 1000, ground_material));

    for (int a = -11; a < 11; a++) {
        for (int b = -11; b < 11; b++) {
            auto choose_mat = random_double();
            point3 center(a + 0.9 * random_double(), 0.2, b + 0.9 * random_double());

            if ((center - point3(4, 0.2, 0)).length() > 0.9) {
                shared_ptr<material> sphere_material;

                if (choose_mat < 0.8) {
                    // diffuse
                    auto albedo = random_vec() * random_vec();
                    sphere_material = make_shared<lambertian>(albedo);
                    // 移动的小球
                    auto center2 = center + vec3(0, random_double(0, 0.5), 0);
                    world.add(make_shared<sphere>(
                        center, center2, 0.0, 1.0, 0.2, sphere_material));
                }
                else if (choose_mat < 0.9) {
                    // metal
                    auto albedo = random_vec(0.5, 1);
                    auto fuzz = random_double(0, 0.5);
                    sphere_material = make_shared<metal>(albedo, fuzz);
                    world.add(make_shared<sphere>(
                        center, center, 0.0, 1.0, 0.2, sphere_material));
                }
                else {
                    // glass
                    sphere_material = make_shared<dielectric>(1.5);
                    world.add(make_shared<sphere>(
                        center, center, 0.0, 1.0, 0.2, sphere_material));
                }
            }
        }
    }

    auto material1 = make_shared<dielectric>(1.5);
    world.add(make_shared<sphere>(
        point3(0, 1, 0), point3(0, 1, 0), 0.0, 1.0, 1.0, material1));

    auto material2 = make_shared<lambertian>(color(0.4, 0.2, 0.1));
    world.add(make_shared<sphere>(
        point3(-4, 1, 0), point3(-4, 1, 0), 0.0, 1.0, 1.0, material2));

    auto material3 = make_shared<metal>(color(0.7, 0.6, 0.5), 0.0);
    world.add(make_shared<sphere>(
        point3(4, 1, 0), point3(4, 1, 0), 0.0, 1.0, 1.0, material3));

    return world;
}

// 两个球体场景
hittable_list two_spheres() {
    hittable_list objects;

    auto checker = make_shared<checker_texture>(color(0.2, 0.3, 0.1), color(0.9, 0.9, 0.9));

    objects.add(make_shared<sphere>(point3(0, -10, 0), 10, make_shared<lambertian>(checker)));
    objects.add(make_shared<sphere>(point3(0, 10, 0), 10, make_shared<lambertian>(checker)));

    return objects;
}

然后修改主函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
...
    
/*******创建场景*******/
hittable_list world;

point3 lookfrom;
point3 lookat;
auto vfov = 40.0;
auto aperture = 0.0;

switch (0) {
    case 1:
        world = random_scene();
        lookfrom = point3(13, 2, 3);
        lookat = point3(0, 0, 0);
        vfov = 20.0;
        aperture = 0.1;
        break;

    default:
    case 2:
        world = two_spheres();
        lookfrom = point3(13, 2, 3);
        lookat = point3(0, 0, 0);
        vfov = 20.0;
        break;
}

/*******创建相机*******/
vec3 vup(0, 1, 0);
auto dist_to_focus = 10.0;

camera cam(lookfrom, lookat, vup, vfov, aspect_ratio, aperture, dist_to_focus, 0.0, 1.0);

...

效果如下：

TwoSphere

---- 本文结束 知识又增加了亿点点！----

文章版权声明 1、博客名称：LycTechStack
2、博客网址：https://lz328.github.io/LycTechStack.github.io/
3、本博客的文章部分内容可能来源于网络，仅供大家学习与参考，如有侵权，请联系博主进行删除处理。
4、本博客所有文章版权归博主所有，如需转载请标明出处。
相关文章