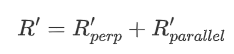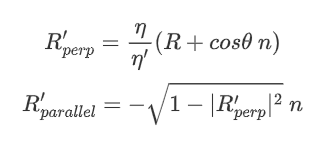【RayTracer】（六）电介质

这一节开始实现诸如水、玻璃、钻石等透明材质，他们都是电介质（dielectric ），光线到达电介质会发生折射，因此首先要计算折射光线。

1 折射光线

之前在图形学中我们知道，Snell‘s law 描述了折射光线和入射光线之间存在关系：
$$
\eta·sin\theta = \eta’·sin\theta’
$$

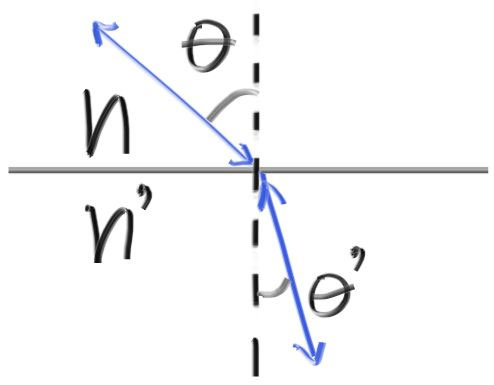
所以求解折射光线就是求解折射角 $\theta’$，$\theta’$ 是折射光线 $R’$ 和法线的夹角，我们可以把 $R’$ 分解为垂直于法线的分量和平行于法线的分量 ：

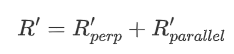
然后可以根据两个分量的计算公式得到折射光线：

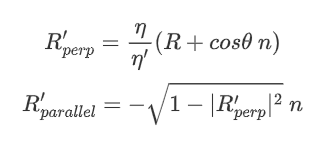
其中 $cos\theta$ 可以通过归一化的入射光线和法线的点乘得到，因此垂直分量可以改写为：
$$
R’_{perp} = \frac{\eta}{\eta’}(R + (-R·n) \ n)
$$
由此我们可以编写一个计算折射光线的函数：

// 计算折射光线
inline vec3 refract(const vec3& R, const vec3& n, double etai_over_etat) {
    auto cos_theta = fmin(dot(-R, n), 1.0);
    vec3 r_out_perp = etai_over_etat * (R + cos_theta * n);
    vec3 r_out_parallel = -sqrt(fabs(1.0 - r_out_perp.length_squared())) * n;
    return r_out_perp + r_out_parallel;
}

2 电介质材质

有了折射光线计算，我们可以实现一个只计算折射光线的电介质材质：

// 电介质材质类
class dielectric : public material {
public:
    dielectric(double index_of_refraction) : ir(index_of_refraction) {}

    virtual bool scatter(
        ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
    ) const override {
        // 电介质不吸收任何光，全部被折射或者反射，所以衰减系数恒为1
        attenuation = color(1.0, 1.0, 1.0);
        // 如果是正面，则是从空气进入介质，反之从介质折射出去
        double refraction_ratio = rec.front_face ? (1.0 / ir) : ir;
        // 入射光线记得单位化，折射函数传入的参数都是单位向量
        vec3 unit_direction = normalize(r_in.direction());
        vec3 refracted = refract(unit_direction, rec.normal, refraction_ratio);

        scattered = ray(rec.p, refracted);
        return true;
    }

public:
    double ir;  //介质折射率
};

然后修改场景，将中间和左边的球体材质更换为电介质，设置折射率为1.5，模拟玻璃材质：

/*******创建场景*******/
hittable_list world;
auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto material_center = make_shared<dielectric>(1.5);
auto material_left = make_shared<dielectric>(1.5);
auto material_right = make_shared<metal>(color(0.8, 0.6, 0.2), 1.0);
world.add(make_shared<sphere>(point3(0.0, -100.5, -1.0), 100.0, material_ground));
world.add(make_shared<sphere>(point3(0.0, 0.0, -1.0), 0.5, material_center));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), 0.5, material_left));
world.add(make_shared<sphere>(point3(1.0, 0.0, -1.0), 0.5, material_right));

得到的结果如下：

这看起来显然是不对的，因为我们现在只计算了折射光线，但是当介质折射率较大的时候，有可能存在无法发生折射的情况，也就是 $\theta’$ 无解，比如上面的玻璃，折射率为 1.5，那么：
$$
sin\theta’ = \frac{1.5}{1}sin\theta
$$
可能出现 $sin\theta’$ 大于 1 的情况，此时不会发生折射，这个现象我们在图形学中也有学过。

因此我们需要在材质的散射函数中做一个判断：

if (refraction_ratio * sin_theta > 1.0) {
    // 折射
    ...
} else {
    // 反射
    ...
}

于是修改我们的电介质材质类：

// 电介质材质类
class dielectric : public material {
public:
    dielectric(double index_of_refraction) : ir(index_of_refraction) {}

    virtual bool scatter(
        ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
    ) const override {
        // 电介质不吸收任何光，全部被折射或者反射，所以衰减系数恒为1
        attenuation = color(1.0, 1.0, 1.0);
        // 如果是正面，则是从空气进入介质，反之从介质折射出去
        double refraction_ratio = rec.front_face ? (1.0 / ir) : ir;
        // 入射光线记得单位化，折射函数传入的参数都是单位向量
        vec3 unit_direction = normalize(r_in.direction());
        // 计算是否发生折射
        double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
        double sin_theta = sqrt(1.0 - cos_theta * cos_theta);

        bool cannot_refract = refraction_ratio * sin_theta > 1.0;
        vec3 direction;

        if (cannot_refract)
            direction = reflect(unit_direction, rec.normal);
        else
            direction = refract(unit_direction, rec.normal, refraction_ratio);

        scattered = ray(rec.p, direction);
        return true;
    }

public:
    double ir;  //介质折射率
};

然后修改场景中的材质：

auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto material_center = make_shared<lambertian>(color(0.1, 0.2, 0.5));
auto material_left = make_shared<dielectric>(1.5);
auto material_right = make_shared<metal>(color(0.8, 0.6, 0.2), 0.0);

得到的效果如下：

3 加入菲涅尔项

现在为电介质材质加入菲涅尔项，使其随着观察角度变化发生更多的反射，依然使用 Schlick’s 近似计算菲涅尔项，修改后的最终材质类如下：

// 电介质材质类
class dielectric : public material {
public:
    dielectric(double index_of_refraction) : ir(index_of_refraction) {}

    virtual bool scatter(
        ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
    ) const override {
        // 电介质不吸收任何光，全部被折射或者反射，所以衰减系数恒为1
        attenuation = color(1.0, 1.0, 1.0);
        // 如果是正面，则是从空气进入介质，反之从介质折射出去
        double refraction_ratio = rec.front_face ? (1.0 / ir) : ir;
        // 入射光线记得单位化，折射函数传入的参数都是单位向量
        vec3 unit_direction = normalize(r_in.direction());
        // 计算是否发生折射
        double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
        double sin_theta = sqrt(1.0 - cos_theta * cos_theta);

        bool cannot_refract = refraction_ratio * sin_theta > 1.0;
        vec3 direction;

        if (cannot_refract || reflectance(cos_theta, refraction_ratio) > random_double())
            direction = reflect(unit_direction, rec.normal);
        else
            direction = refract(unit_direction, rec.normal, refraction_ratio);

        scattered = ray(rec.p, direction);
        return true;
    }

public:
    double ir;  //介质折射率

private:
    static double reflectance(double cosine, double ref_idx) {
        // 使用Schlick's近似计算菲涅尔项
        auto r0 = (1 - ref_idx) / (1 + ref_idx);
        r0 = r0 * r0;
        return r0 + (1 - r0) * pow((1 - cosine), 5);
    }
};

我们现在实现的电介质材质类是简化后的版本，光线打到物体上要么发生反射，要么发生折射，我们并没有同时考虑折射光线和反射光线。

4 空心玻璃球

对于玻璃球来说，如果使用负半径，几何形状不受影响，但表面法线指向内（可以回顾球体类中 hit 方法的实现）。这可以作为一个气泡来制作一个中空的玻璃球：

hittable_list world;
auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto material_center = make_shared<lambertian>(color(0.1, 0.2, 0.5));
auto material_left = make_shared<dielectric>(1.5);
auto material_right = make_shared<metal>(color(0.8, 0.6, 0.2), 0.3);
world.add(make_shared<sphere>(point3(0.0, -100.5, -1.0), 100.0, material_ground));
world.add(make_shared<sphere>(point3(0.0, 0.0, -1.0), 0.5, material_center));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), 0.5, material_left));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), -0.4, material_left));
world.add(make_shared<sphere>(point3(1.0, 0.0, -1.0), 0.5, material_right));

我们向场景中左边球体内加了一个同心半径为负的球体，使它们构成了一个空心玻璃球，渲染效果如下：