【RayTracer】（四）漫反射材质

现在我们已经有了光线和物体，接下来可以实现一些看起来更加真实的效果，从漫反射材质开始。

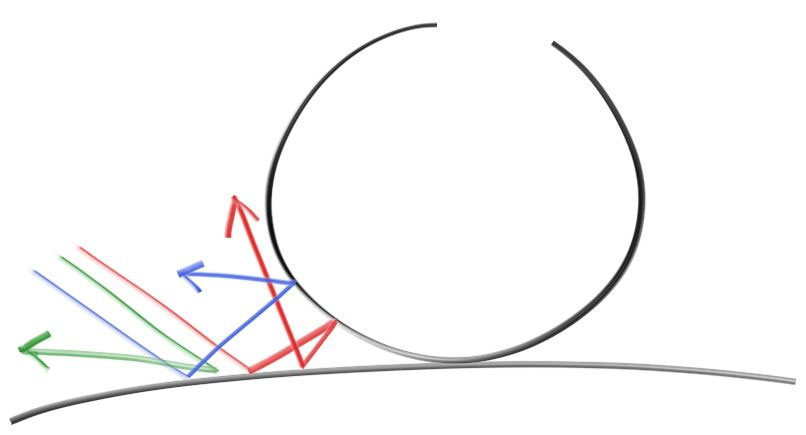
1 简单的漫反射材质

回顾漫反射的形成原理，光线打到物体表面后一部分光会折射进入物体，并在物体内部发生各种次表面散射后从物体表面的某个方向再折射出去，因此漫反射的颜色主要取决于环境光颜色，并用物体自身的颜色去调节这些来自环境的光线，因此也可以认为漫反射反映了物体自身的颜色。从宏观来看漫反射就像是光线向各个方向均匀散射，而在我们的简单实现中可以认为光线在物体表面的反射方向是随机的，比如三根光线打到两个物体的夹缝处，他们可能产生完全不同的行为：

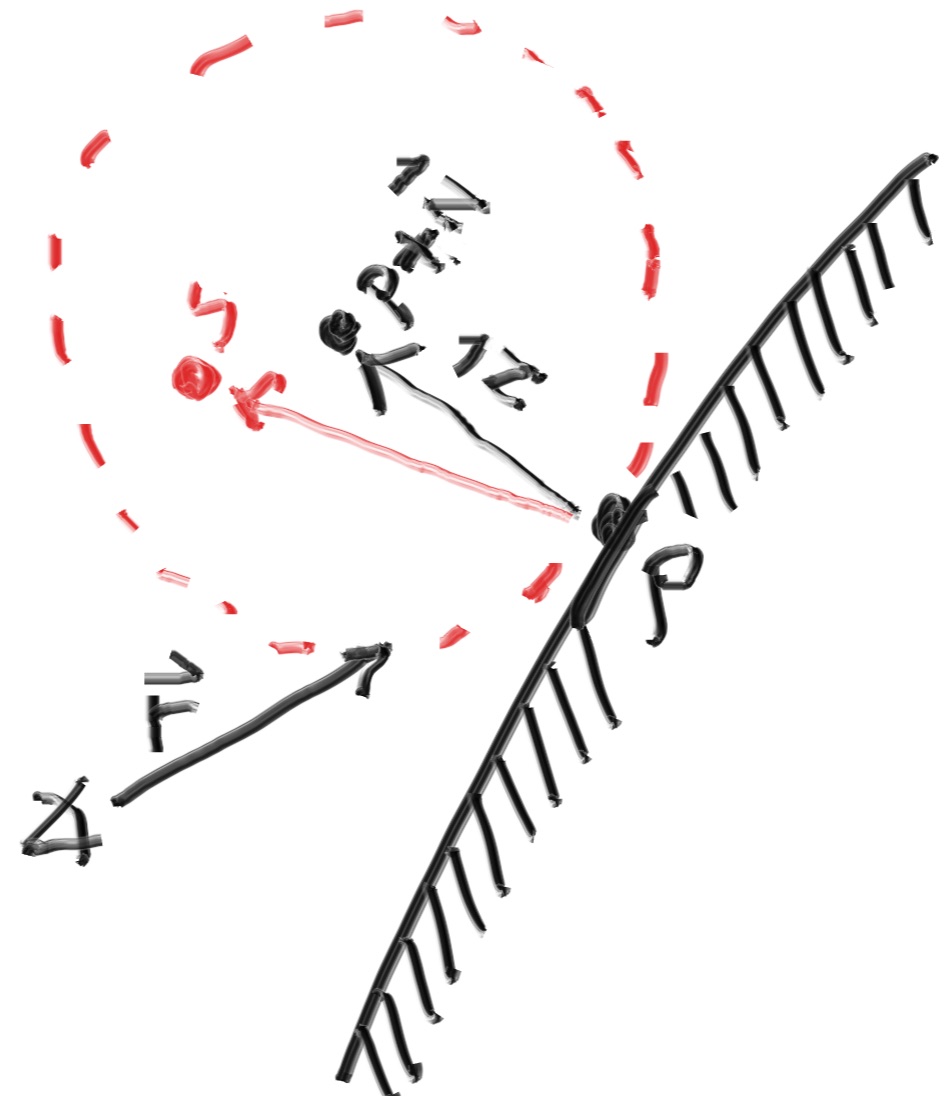
因此要模拟漫反射材质，我们首先要能够随机生成漫反射弹射光线。可以使用如下方法生成：

光线与物体表面相交于一点 $p$
在 $p + \vec n$ 处构造一个与点 $p$ 相切的单位球体，其中 $\vec n$ 是点 $p$ 处的法线
随机在单位球体中选择一点 $s$ ，漫反射弹射光线的方向就是 $s - p = \vec{ps}$

为此我们要先增加一些工具函数用于在单位球体内生成随机点，由于直接生成单位球体内的点并不是很方便实现，我们可以先生成单位立方体内的点，即三个维度的坐标都在 [-1, 1] 范围内，然后判断该点是否在球体内，如果不在球体内就重新随机选择，直到满足条件。

//utilities.h

...

// 生成分量在[0,1]之间的随机向量
inline vec3 random_vec() {
    return vec3(random_double(), random_double(), random_double());
}

// 生成分量在[min,max]之间的随机向量
inline vec3 random_vec(double min, double max) {
    return vec3(random_double(min, max), random_double(min, max), random_double(min, max));
}

// 生成单位球体内随机一点
inline point3 random_in_unit_sphere() {
    while (true) {
        auto p = random_vec(-1, 1);
        if (p.length_squared() >= 1) continue;
        return p;
    }
}

然后修改 ray_color 函数：

// 得到光线颜色
color ray_color(ray& r, const hittable& world) {
    hit_record rec;
    // 计算漫反射颜色
    if (world.hit(r, 0, infinity, rec)) {
        // 随机选择漫反射光线弹射方向
        point3 target = rec.p + rec.normal + random_in_unit_sphere();
        ray bounce = ray(rec.p, target - rec.p);
        // 只有0.5的光线发生下一次弹射，其他的被吸收
        return 0.5 * ray_color(bounce, world);
    }
    vec3 unit_direction = normalize(r.direction());
    auto t = 0.5 * (unit_direction.y() + 1.0);
    return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}

这样就可以递归的计算光线弹射多次所得到的漫反射颜色了。

2 限制光线弹射次数

上面的实现中，没有递归结束的条件，也就是限制光线弹射的次数，因此需要加一个递归深度来限制光线的弹射次数：

// 得到光线颜色
color ray_color(ray& r, const hittable& world, int depth) {
    hit_record rec;
    // 限制弹射次数
    if (depth <= 0) return color(0, 0, 0);
    // 计算漫反射颜色
    if (world.hit(r, 0, infinity, rec)) {
        // 随机选择漫反射光线弹射方向
        point3 target = rec.p + rec.normal + random_in_unit_sphere();
        ray bounce = ray(rec.p, target - rec.p);
        // 只有0.5的光线发生下一次弹射，其他的被吸收
        return 0.5 * ray_color(bounce, world, depth - 1);
    }
    vec3 unit_direction = normalize(r.direction());
    auto t = 0.5 * (unit_direction.y() + 1.0);
    return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}

然后修改主函数：

#include <iostream>
#include <string>
#define STB_IMAGE_WRITE_IMPLEMENTATION
#include "stb_image_write.h"
#include "hittable_list.h"
#include "sphere.h"
#include "color.h"
#include "camera.h"

int main()
{
    /****图片保存，保存为png格式****/
    std::string SavePath = "D:\\TechStack\\ComputerGraphics\\Ray Tracing in One Weekend Series\\Results\\";
    std::string filename = "Diffuse.png";
    std::string filepath = SavePath + filename;
    
    /*******图片属性*******/ 
    const auto aspect_ratio = 16.0 / 9.0;
    const int image_width = 400;
    const int image_height = static_cast<int>(image_width / aspect_ratio);
    const int channel = 3;
    const int samples_per_pixel = 100;
    // 光线弹射次数
    const int max_depth = 50;

    /*******创建相机*******/
    camera cam;

    /*******创建场景*******/
    hittable_list world;
    world.add(make_shared<sphere>(point3(0, 0, -1), 0.5));
    world.add(make_shared<sphere>(point3(0, -100.5, -1), 100));

    /******渲染部分*****/
    unsigned char* odata = (unsigned char*)malloc(image_width * image_height * channel);
    unsigned char* p = odata;
    for (int j = image_height - 1; j >= 0; --j) {
        std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
        for (int i = 0; i < image_width; ++i) {
            color pixel_color(0, 0, 0);
            for (int s = 0; s < samples_per_pixel; ++s) {
                // 在像素内部随机采样
                auto u = (i + random_double()) / (image_width - 1);
                auto v = (j + random_double()) / (image_height - 1);
                ray r = cam.get_ray(u, v);
                pixel_color += ray_color(r, world, max_depth);
            }
            write_color(p, pixel_color, samples_per_pixel);
        }
    }
    stbi_write_png(filepath.c_str(), image_width, image_height, channel, odata, 0);
    std::cerr << "\nDone.\n";
}

得到如下效果：

使用固定弹射次数会导致很多没用的计算，仅仅渲染上面这样一张图就要用掉近三分钟，效率非常低，并且固定弹射次数会影响最终渲染效果。之前在图形学中我们学习过，更好的限制光线弹射次数的方法是使用俄罗斯轮盘赌算法（RR），该算法在保证期望正确的情况下大幅提高了渲染效率，因此我们用 RR 算法来限制光线弹射次数：

// 得到光线颜色
color ray_color(ray& r, const hittable& world) {
    hit_record rec;
    // 俄罗斯轮盘赌的生存概率
    auto RR = 0.8;
    // 计算漫反射颜色
    // 这里的t的下界设为0.001是为了防止一些光线弹射到物体上得到的t非常接近0，比如可能出现0.000001这样的值
    if (world.hit(r, 0.001, infinity, rec)) {
        // 以一定概率停止弹射
        if (random_double() >= RR) return color(0, 0, 0);
        // 随机选择漫反射光线弹射方向
        point3 target = rec.p + rec.normal + random_in_unit_sphere();
        ray bounce = ray(rec.p, target - rec.p);
        // 要记得除以生存概率才能得到正确的期望
        return 0.5 * ray_color(bounce, world) / RR;
    }
    vec3 unit_direction = normalize(r.direction());
    auto t = 0.5 * (unit_direction.y() + 1.0);
    return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}

主函数中之前做的修改可以 Ctrl + Z 了，现在无需做任何修改，得到的效果如下：

渲染这张图只用了不到 20 秒，效率大幅提升并且渲染效果更好。

3 伽马校正

在上面的例子中我们设置了一半的光线被吸收，一半的光线被反射，在现实中这个球体看起来应该更亮一些，呈现灰色，但上面的渲染结果中球体颜色非常暗，尤其是球体下的阴影处，这是因为我们没有进行伽马校正（Gamma Correction）。

伽马校正中的伽马一词来源伽马曲线。通常，伽马曲线的表达式如下：
$$
L_{out} = L_{in}^\gamma
$$
其中指数部分的发音就是伽马。最开始的时候，人们使用伽马曲线来对拍摄的图像进行伽马编码。事情的起因可以从在真实环境中拍摄一张图片说起。摄像机的原理可以简化为，把进入到镜头内的光线亮度编码成图像中的像素。如果采集到的亮度是 0，像素就是 0，亮度是 1，像素就是 1，亮度是 0.5，像素就是 0.5。如果我们只用 8 位空间来存储像素的每个通道的话，这意味着 0~1 区间可以对应 256 种不同的亮度值。但是，后来人们发现，人眼有一个有趣的特性，就是对光的灵敏度在不同亮度上是不一样的。在正常的光照条件下，人眼对较暗区域的变化更加敏感，如下图：

颜色越暗，我们就感觉从左到右的变化越明显。所以亮度上的线性变化对人眼的感知来说是非均匀的。

另一个例子可以说明这个现象，当一个屋子的光照由一盏灯增加到两盏灯的时候，人眼对这种亮度变化的感知性要远远大于从 101 盏灯增加到 102 盏灯的变化，但是从物理上来说这两种变化基本是相同的。

所以，如果使用 8 位空间来存储每个通道的话，我们仍然把 0.5 亮度编码成值为 0.5 的像素，那么暗部和亮部区域我们都使用了 128 种颜色来表示，但实际上，对亮部区域使用这么多颜色是种存储浪费。一种更好的方法是，我们应该把把更多的空间来存储更多的暗部区域，这样存储空间就可以被充分利用起来了。摄影设备如果使用了 8 位空间来存储照片的话，会使用大约为 0.45 的编码伽马来对输入的亮度进行编码，得到一张编码后的图像。因此，图像中 0.5 像素值对应的亮度其实并不是 0.5，而大约为 0.22。这是因为：
$$
0.5 \approx 0.22^{0.45}
$$
如上所见，对拍摄图像使用的伽马编码使得我们可以充分利用图像的存储空间。但当把图片放到显示器里显示时，我们应该对图像再进行一次解码操作，使得屏幕输出的亮度和捕捉到的亮度是符合线性的。

这时，人们发现了一个奇妙的巧合—— CRT 显示器本身几乎已经自动做了这个解码操作。在早期，CRT（Cathode Ray Tube，阴极射线管）几乎是唯一的显示设备。这类设备的显示机制是，使用一个电压轰击它屏幕上的一种图层，这个图层就可以发亮，我们就可以看到图像了。但 CRT 显示器有一个特性，它的输入电压和显示出来的亮度关系不是线性的，也就是说，如果我们把输入电压调高两倍，屏幕亮度并没有提高两倍。我们把显示器的这个伽马曲线称为**显示伽马 (diplay gamma)**。非常巧合的是，CRT 的显示伽马值大约就是编码伽马的倒数。CRT 显示器的这种特性，正好补偿了图像捕捉设备的伽马曲线。虽然现在 CRT 设备很少见了，并且后来出现的显示设备有着不同的伽马响应曲线，但是，人们仍在硬件上做了调整来提供兼容性。

随后，微软联合爱普生、惠普提供了 sRGB 颜色空间标准，推荐显示器的显示伽马值为 2.2，并配合 0.45 的编码伽马就可以保证最后伽马曲线之间可以相互抵消（因为 $2.2 \times 0.45 \approx 1$ ）。绝大多数的摄像机、 PC 和打印机都使用了上述的 sRGB 标准。

对于我们的渲染来说，如果我们直接输出渲染结果而不做任何处理，在经过显示器的显示伽马处理后，就会导致颜色偏暗的现象。因此我们在计算像素颜色时有必要进行伽马校正。

为了简化计算我们假设显示伽马为 2.0，因此我们的编码伽马为 0.5，在写入像素的时候对像素的最终颜色值进行伽马编码，就可以让颜色显示正常了：

// 输入的color是[0,1]范围的
inline void write_color(unsigned char*& p, color pixel_color, int samples_per_pixel)
{
    auto r = pixel_color.x();
    auto g = pixel_color.y();
    auto b = pixel_color.z();

    auto scale = 1.0 / samples_per_pixel;

    // 伽马校正，假设显示gamma=2.0
    r = sqrt(scale * r);
    g = sqrt(scale * g);
    b = sqrt(scale * b);

    *p++ = (unsigned char)(256 * clamp(r, 0.0, 0.999));
    *p++ = (unsigned char)(256 * clamp(g, 0.0, 0.999));
    *p++ = (unsigned char)(256 * clamp(b, 0.0, 0.999));
}

经过伽马矫正后的渲染结果如下：

4 True Lambertian Reflection

现在回顾上面在单位球体内选取随机点的实现。这样的实现会使得选取到的随机反射方向大概率接近法线，而以很小的概率接近掠射角方向，这是因为整个球体中大部分位置和表面交点的连线都接近法线方向，只有很小一部分接近掠射角方向，这代表我们随机选取的反射方向不是均匀分布的，但这似乎是合理的，因为越接近掠射角代表光线越接近该交点的切线方向，所以对最终颜色的贡献也更小。

而 True Lambertian Reflection 并不是这样的， True Lambertian Reflection 的随机方向更均匀，因为它是在单位球面上随机取点并构成反射方向，这样显然随机选取的反射方向会更加均匀。

我们可以通过先在球面内随机取点，并将其单位化，以得到球面上随机一点：

// 生成单位球面上随机一点
inline vec3 random_unit_vector() {
    return normalize(random_in_unit_sphere());
}

然后修改 ray_color 部分：

color ray_color(ray& r, const hittable& world) {
    hit_record rec;
    auto RR = 0.8;
    if (world.hit(r, 0.001, infinity, rec)) {
        if (random_double() >= RR) return color(0, 0, 0);
        // 这次使用球面上的随机点
        //point3 target = rec.p + rec.normal + random_in_unit_sphere();
        point3 target = rec.p + rec.normal + random_unit_vector();
        ray bounce = ray(rec.p, target - rec.p);
        return 0.5 * ray_color(bounce, world) / RR;
    }
    vec3 unit_direction = normalize(r.direction());
    auto t = 0.5 * (unit_direction.y() + 1.0);
    return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}

得到的效果如下：

可以注意到和之前的结果中两个不同的视觉变化：

阴影变得不那么明显了
物体变得稍微亮了一点

这两种变化都是由于光线散射更均匀，向法线附近散射的光线更少而产生的。对于漫反射物体，它们会显得更亮是因为更多的光线会反射到相机上。对于阴影，因为向法线附近散射的光线更少，所以大球体表面和上面的小球体的夹缝处就会有更多的光线散射出去，而不是在夹缝处一直弹射。

5 另一种散射方法

除了上面的在球体内随机取点和在球面上随机取点之外，还有一种随机散射的方法。在之前的方法中我们选取了一个单位球，这个单位球的球心相比于光线和表面的交点偏移了一个法线，但很难解释我们为什么这么做。一个更直观的方法是不进行法线偏移，在单位球体内随机取一点作为光线和物体的交点 p 的偏移，然后用偏移后的点 p 和原来的点 p 构成随机反射方向。这相当于以 p 为球心，在一个半球上随机取点构成反射方向，在实现中要注意如果偏移后的点 p 落入了下半球，意味着反射光线指向了物体内部，这是错误的，此时要对偏移量取反，以保证反射光线和该点的法线在同一个半球。

// 在半球内随机取点
inline vec3 random_in_hemisphere(const vec3& normal) {
    vec3 in_unit_sphere = random_in_unit_sphere();
    // 判断该偏移量是否落入了下半球，如果落入下半球则偏移量应该取反
    if (dot(in_unit_sphere, normal) > 0.0)
        return in_unit_sphere;
    else
        return -in_unit_sphere;
}

然后修改 ray_color 部分：

// 得到光线颜色
color ray_color(ray& r, const hittable& world) {
    hit_record rec;
    auto RR = 0.8;
    if (world.hit(r, 0.001, infinity, rec)) {
        if (random_double() >= RR) return color(0, 0, 0);
        // 在法线偏移的单位球体内部随机取一点得到反射方向
        //point3 target = rec.p + rec.normal + random_in_unit_sphere();
        // 在法线偏移的单位球体表面随机取一点得到反射方向
        //point3 target = rec.p + rec.normal + random_unit_vector();
        // 在以交点为球心的半径为 1 的半球内随机取一点得到反射方向
        point3 target = rec.p + random_in_hemisphere(rec.normal);
        ray bounce = ray(rec.p, target - rec.p);
        return 0.5 * ray_color(bounce, world) / RR;
    }
    vec3 unit_direction = normalize(r.direction());
    auto t = 0.5 * (unit_direction.y() + 1.0);
    return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}

得到的效果如下：

以上三种散射方法没有对错之分，在后面场景变得越来越复杂之后，可以通过尝试切换这三种漫反射渲染器来观察不同的方法对渲染效果的影响。