【RayTracer】（一）实现基本工具类

这部分我们将使用 C++ 从零开始实现一个光线追踪器。首先需要实现一些在简单的光线追踪器中要用到的基本工具类，包含三维向量类、光线类，以及一些之后可能频繁用到的工具函数。

1 三维向量类

尽管在正规的光线追踪器中使用更多的是四维向量，比如齐次坐标和带有 A 通道的颜色，但是对于我们这个简化的光线追踪器来说，三维向量已经足够了，我们可以使用三维向量表示位置、方向、颜色等，为了区分这三种表示，我们给三维向量类 vec3起两个别名 point3 和 color 以方便之后代码的编写和阅读，但他们实质上没有任何区别，我们没有为了不同的表示构造一个专门的类，这意味着一个颜色和一个位置可以进行相加，这在正常的光线追踪工程实现中是不被允许的，但我们毕竟是简化版本，只要在使用的时候注意即可。

我们首先在该类中实现一些基本的方法：

/*
  实现三维向量类，用于存储位置、向量、颜色等
*/
#pragma once
#ifndef VEC3_H
#define VEC3_H

#include <cmath>
#include <iostream>

using std::sqrt;

// 定义类及常用方法
class vec3
{
public:
    double e[3];
public:
    vec3() : e{ 0,0,0 } {}
    vec3(double e0, double e1, double e2) : e{ e0, e1, e2 } {}

    double x() const { return e[0]; }
    double y() const { return e[1]; }
    double z() const { return e[2]; }

    vec3 operator-() const { return vec3(-e[0], -e[1], -e[2]); }
    double operator[](int i) const { return e[i]; }
    double& operator[](int i) { return e[i]; }

    vec3& operator+=(const vec3& v) {
        e[0] += v[0];
        e[1] += v[1];
        e[2] += v[2];
        return *this;
    }

    vec3& operator*=(const double t) {
        e[0] *= t;
        e[1] *= t;
        e[2] *= t;
        return *this;
    }

    vec3& operator/=(const double t) {
        return *this *= 1/t;
    }

    double length_squared() const {
        return e[0] * e[0] + e[1] * e[1] + e[2] * e[2];
    }

    double length() const {
        return sqrt(length_squared());
    }
};

// 定义vec3的别名，分别用于存储点和颜色，提升代码可读性
using point3 = vec3;
using color = vec3;

#endif

在工程实践中，文件开头的 #pragma once 是必须的，否则可能因为头文件重复包含导致编译错误，定义类时的判断：

#ifndef VEC3_H
#define VEC3_H

...

#endif

也是必须的，同样是为了防止重复编译。

然后实现一些对向量操作的工具函数，大部分是运算符重载，以让我们可以按照之前的习惯操作三维向量：

/*******一些工具函数*******/
inline std::ostream& operator<<(std::ostream& out, const vec3& v) {
    return out << v.e[0] << ' ' << v.e[1] << ' ' << v.e[2];
}

inline vec3 operator+(const vec3& u, const vec3& v) {
    return vec3(u.e[0] + v.e[0], u.e[1] + v.e[1], u.e[2] + v.e[2]);
}

inline vec3 operator-(const vec3& u, const vec3& v) {
    return vec3(u.e[0] - v.e[0], u.e[1] - v.e[1], u.e[2] - v.e[2]);
}

// 对应元素相乘
inline vec3 operator*(const vec3& u, const vec3& v) {
    return vec3(u.e[0] * v.e[0], u.e[1] * v.e[1], u.e[2] * v.e[2]);
}
// 向量和标量运算
inline vec3 operator*(double t, const vec3& v) {
    return vec3(t * v.e[0], t * v.e[1], t * v.e[2]);
}
inline vec3 operator*(const vec3& v, double t) {
    return t * v;
}
inline vec3 operator/(const vec3& v, double t) {
    return (1 / t) * v;
}
// 点乘
inline double dot(const vec3& u, const vec3& v) {
    return u.e[0] * v.e[0] + u.e[1] * v.e[1] + u.e[2] * v.e[2];
}
// 叉乘
inline vec3 cross(const vec3& u, const vec3& v) {
    return vec3(u.e[1] * v.e[2] - u.e[2] * v.e[1],
        u.e[2] * v.e[0] - u.e[0] * v.e[2],
        u.e[0] * v.e[1] - u.e[1] * v.e[0]);
}
// 单位化
inline vec3 normalize(vec3 v) {
    return v / v.length();
}

// 向数组中写入一个颜色，用于最后的图像输出，用到了指针的引用传递
// 注意输入的color是[0,1]范围的
void write_color(unsigned char*& p, color pixel_color)
{
    *p++ = (unsigned char)(255.999 * pixel_color.x());
    *p++ = (unsigned char)(255.999 * pixel_color.y());
    *p++ = (unsigned char)(255.999 * pixel_color.z());
}

2 光线类

光线类是基于三维向量类的，我们按照图形学中射线的定义来实现一个光线类，给定空间中一个位置和一个方向就可以确定一条射线，再给定时间 t，就可以得到射线上任意一点：

/*
    实现光线类
*/
#pragma once
#ifndef RAY_H
#define RAY_H

#include "vec3.h"

class ray
{
public:
    ray() {}
    ray(const point3& origin, const vec3& direction) :
        orig(origin), dir(direction) {}

    point3 origin() { return orig; }
    vec3 direction() { return dir; }

    point3 at(double t) const {
        return orig + t * dir;
    }

public:
    point3 orig;
    vec3 dir;
};

#endif

3 图像输出

我们所有渲染结果最终都要输出到一张图片中，我们可以选择任何输出格式，这里使用了非常方便的开源的图像工具 stb_image ，将结果保存到数组中然后使用 stbi_write_png 函数保存为 PNG 格式图片。我们用一个生成渐变图片的例子来了解图像输出流程。

首先定义一个 ray_color 函数，根据给定的方向机型简单的线性插值，以混合两种不同的颜色：

// 根据归一化的方向的y坐标线性混合白色和蓝色，以得到自上而下的蓝白色渐变效果
color ray_color(ray& r)
{
    vec3 unit_dir = normalize(r.direction());
    // 归一化后y的范围是[-1,1]，将其映射到[0,1]作为混合系数
    auto t = 0.5 * (unit_dir.y() + 1.0);
    return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}

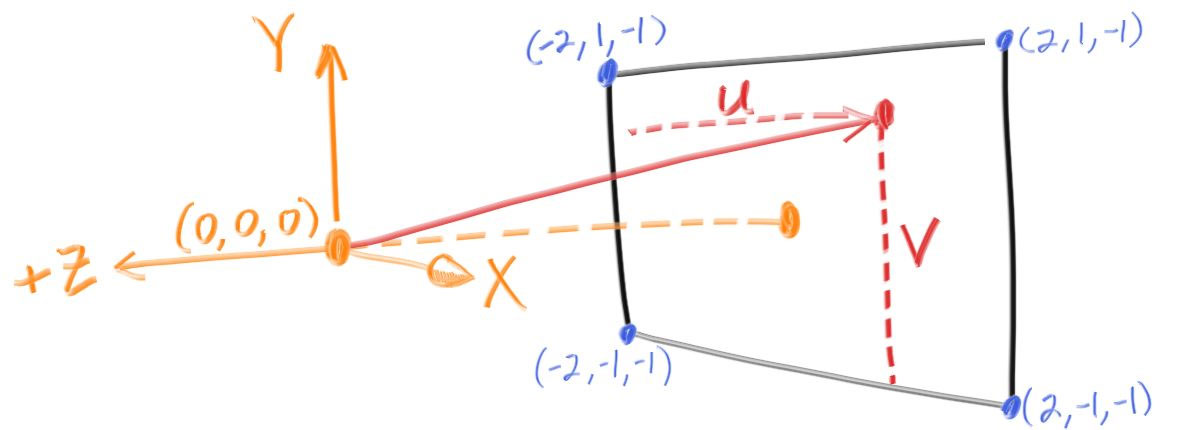
我们定义相机所在位置为 (0, 0, 0)，屏幕（输出的图片）比例为 16 : 9，因此我们的视口比例也要和最终的图片比例一致，然后从屏幕左上角开始遍历，从相机向屏幕投射光线，根据该光线方向通过 ray_color 函数计算插值颜色显示到屏幕上。场景大致如下：

下面实现主函数：

#include <iostream>
#include <string>
#define STB_IMAGE_WRITE_IMPLEMENTATION
#include "stb_image_write.h"
#include "vec3.h"
#include "ray.h"

int main()
{
    /*******图片属性*******/ 
    // 宽高比
    const auto aspect_ratio = 16.0 / 9.0;
    const int image_width = 400;
    // 使用static_cast可以明确告诉编译器，这种损失精度的转换是在知情的情况下进行的
    // 也可以让阅读程序的其他程序员明确你转换的目的而不是由于疏忽
    const int image_height = static_cast<int>(image_width / aspect_ratio);
    const int channel = 3;

    /*******相机属性*******/
    // 视口高度设为两个单位
    auto viewport_height = 2.0;
    // 视口宽度根据屏幕宽高比计算
    auto viewport_width = aspect_ratio * viewport_height;
    // 原点到视口平面距离为1个单位
    auto focal_length = 1.0;
    // 相机原点
    auto origin = point3(0, 0, 0);
    // 视口宽的一半
    auto horizontal = vec3(viewport_width, 0, 0);
    // 视口高的一半
    auto vertical = vec3(0, viewport_height, 0);
    // 相当于将(0,0,0)移动到视口平面的左下角，也就是得到左下角的点的位置
    auto lower_left_corner = origin - horizontal / 2 - vertical / 2 - vec3(0, 0, focal_length);

    
    /****图片保存，保存为png格式****/
    std::string SavePath = "D:\\TechStack\\ComputerGraphics\\Ray Tracing in One Weekend Series\\Results\\";
    std::string filename = "BlendColor.png";
    std::string filepath = SavePath + filename; 
    // 3通道图像存在一维数组
    unsigned char* odata = (unsigned char*)malloc(image_width * image_height * channel);
    unsigned char* p = odata;

    /******渲染部分*****/
    for (int j = image_height - 1; j >= 0; --j) {
        // 标准错误流显示进度信息，可以刷新显示
        std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
        for (int i = 0; i < image_width; ++i) {
            // x方向偏移
            auto u = double(i) / (image_width - 1);
            // y方向偏移
            auto v = double(j) / (image_height - 1);
            ray r(origin, lower_left_corner + u * horizontal + v * vertical - origin);
            color pixel_color = ray_color(r);
            write_color(p, pixel_color);
        }
    }
    stbi_write_png(filepath.c_str(), image_width, image_height, channel, odata, 0);
    std::cerr << "\nDone.\n";
}

得到的结果如下：