【数据结构】优先队列和堆

优先队列（Priority Queue）是计算机科学中的一类抽象数据类型。优先队列中的每个元素都有各自的优先级，优先级最高的元素最先得到服务；优先级相同的元素按照其在优先队列中的顺序得到服务。堆（Heap）是一种数据结构，是实现优先队列的一种方式。所以堆并不等同于优先队列。

优先队列还有其他的实现方式，比如数组和链表。但是，这些实现方式只能保证插入操作和删除操作中的一种操作可以在 O(1) 的时间复杂度内完成，而另外一个操作则需要在 O(N) 的时间复杂度内完成。堆能够使优先队列的插入操作在 O(log N) 的时间复杂度内完成，删除操作在 O(log N) 的时间复杂度内完成。

1 堆的定义和基本操作

堆是一种特殊的二叉树，满足以下两个条件：

是完全二叉树，所谓完全二叉树是指叶子节点只能出现在最下层和次下层的二叉树，树中每一个结点的编号都和满二叉树一一对应
每一个节点的值都必须大于等于或者小于等于其孩子节点的值

堆具有以下特点：

可以在 O(logN) 的时间复杂度内向堆中插入元素；
可以在 O(logN) 的时间复杂度内在堆中删除元素；
可以在 O(1) 的时间复杂度内获取堆中最大或最小的元素；

堆分为小顶堆和大顶堆两类：

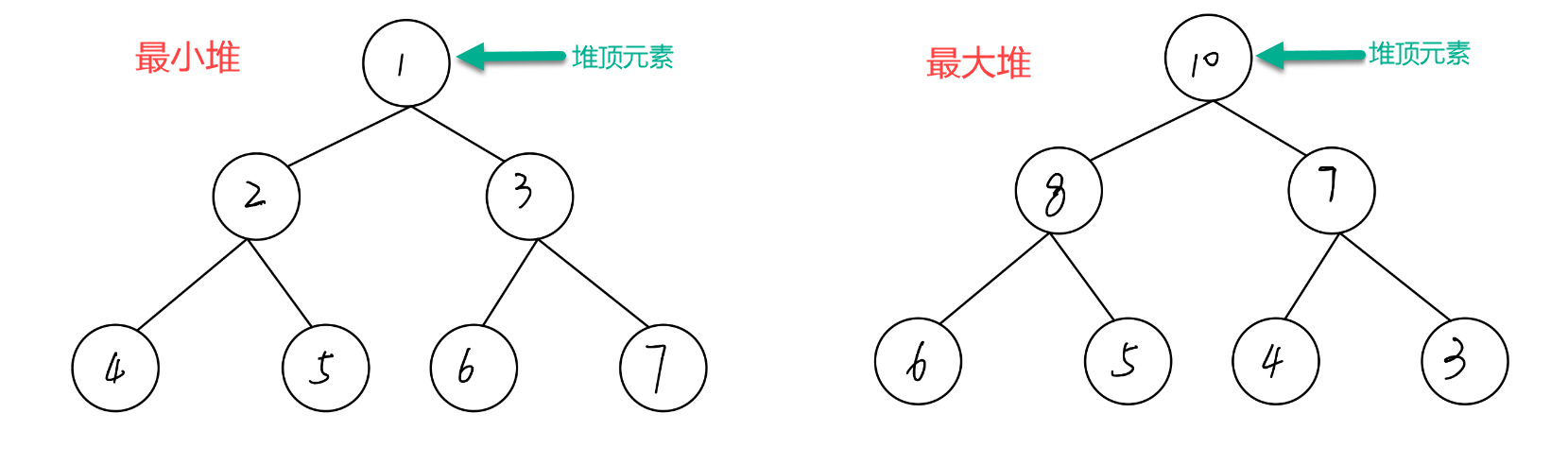
堆的基本操作有插入（在堆中插入一个元素同时保持堆的性质不变）、删除（删除堆顶元素同时保持堆的性质不变）和获取堆顶元素。

在 C++ 中已经有内置方法实现了堆，所以一般来说并不需要我们去实现一个堆。我们只需要掌握堆在 C++ 中的常用方法，使我们能灵活的运用堆去解决问题即可。

C++ STL 实现了对存储在数组或 vector 中的元素进行堆操作的函数，包括创建堆和堆的基本操作：

创建堆：make_heap(_First, _Last, _Comp)，默认是大顶堆
在堆中添加元素：push_heap(_First, _Last, _Comp)，该函数实际上是用来调整堆序的，要先在 vector 中 push_back 一个元素到尾部，然后再使用 push_heap，例如：

1 2	max_heap.push_back(15); push_heap(max_heap.begin(), max_heap.end());

在堆中删除元素：pop_heap(_First, _Last, _Comp)，该函数是删除原本的堆顶元素，并将该元素放到 vector 末尾，用 vector 原来的末尾元素作为新的堆顶元素，因此该函数执行完毕后要取走原本的堆顶元素还要使用 vector.pop_back()，例如：

//取出了堆顶元素（也叫删除堆顶元素），放到了底层容器的末尾，原来末尾的元素替代堆顶，end迭代器减1，重新siftdown了堆
pop_heap(max_heap.begin(), max_heap.end());
//从底层容器（数组或vector）中删除了元素
max_heap.pop_back();

堆排序：sort_heap(_First, _Last, _Comp)，既然每次 pop_heap 可以获得堆顶的元素（假如是大顶堆，每次都获得最大的元素，取出放到了底层容器的末尾），那么我们持续对整个 heap 做 pop_heap 操作，每次将操作的范围向前缩减一个元素（就是每次 end 迭代器减 1 ）。最终我们可以获得一个递增的序列。

下面是基本使用示例：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

void printHeap(vector<int> &v){
    for(vector<int>::iterator it= v.begin();it!=v.end();++it){
        cout<< *it <<" ";
    }
    cout<<"\n"<<endl;
}

int main()
{
    vector<int> min={10,30,22,6,15,9};

    //建立小顶堆
    make_heap(min.begin(), min.end(), greater<int>());
    printHeap(min);//6 10 9 30 15 22

    //插入元素
    min.push_back(20);
    push_heap(min.begin(),min.end(), greater<int>()); //该算法前提：必须在堆的条件下
    printHeap(min); //6 10 9 30 15 22 20  仍为小顶堆

    //删除堆顶元素
    pop_heap(min.begin(),min.end(), greater<int>());
    printHeap(min);//9 10 20 30 15 22 6  不为小顶堆 这个pop_heap操作后，实际上是把堆顶元素放到了末尾
    min.pop_back();//这才彻底在底层vector数据容器中删除
    printHeap(min);//9 10 20 30 15 22  仍为小顶堆

    //堆排序  保持greater，小顶堆，得到的是降序
    sort_heap(min.begin(),min.end(), greater<int>()); //试了用less，结果杂乱无章
    printHeap(min);//30 22 20 15 10 9 注意结果是降序的哦!!!其实是调用了很多次pop_heap(...,greater..)，每一次都把小顶堆堆顶的元素往末尾放，每放一次end迭代器减1

    return 0;
}

如果把上面code里所有的第三个参数改为less<int>()，就是大顶堆和排序为升序。

C++ 中还有优先队列的实现，和普通队列的用法类似，只是在创建时略有不同：

//默认按照元素从大到小的顺序出队
priority_queue<int> q;   　　
//按照元素从小到大的顺序出队，第二个参数是容器类型
priority_queue<int,vector<int>, greater<int> > q; 
//自定义优先级
struct cmp {     
　　operator bool ()(int x, int y)     
　　{        
　　　　 return　x > y;
　　}
};
priority_queue<int, vector<int>, cmp> q;
//结构体声明，重载 < 运算符
struct node {     
　　int x, y;     
　　friend bool operator < (node a, node b)     
　　{         
　　　　return a.x > b.x;    //结构体中，x小的优先级高     
　　}
};
priority_queue<node>q;

2 堆的应用

2.1 堆排序

C++ 中已经提供了堆排序，我们也已经了解了堆排序的过程，之后会在专门的排序算法专题中再次学习堆排序。

2.2 Top K 问题

Top K 问题是最经典的用堆（优先队列）解决的问题。

最小的k个数

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

一种解法是创建小顶堆，然后取 k 次堆顶元素：

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> ans;
        make_heap(arr.begin(), arr.end(), greater<int>());
        for(int i = 0; i < k; ++i)
        {
            pop_heap(arr.begin(), arr.end(), greater<int>());
            ans.push_back(arr.back());
            arr.pop_back();
        }
        return ans;
    }
};

这种方法调用了 K 次删除操作，因此时间复杂度是 O(KlogN)。

另一种解法是创建大顶堆，向堆中添加元素，当堆中有 K 个元素时，每次添加元素前与堆顶元素对比，如果当前元素比堆顶元素大则舍弃，如果当前元素比堆顶元素小，则删除堆顶元素并将当前元素加入堆，这样遍历完整个数组后，堆中的元素就是最小的 k 个元素。

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> ans;
        if(k == 0) return ans;
        make_heap(ans.begin(), ans.end(), less<int>());
        for(int i = 0; i < arr.size(); ++i)
        {
            if(k > 0)
            {
                ans.push_back(arr[i]);
                push_heap(ans.begin(), ans.end(), less<int>());
                --k;
            }
            else
            {
                if(arr[i] < ans[0])
                {
                    pop_heap(ans.begin(), ans.end(), less<int>());
                    ans.pop_back();
                    ans.push_back(arr[i]);
                    push_heap(ans.begin(), ans.end(), less<int>());
                }
            }
        }
        return ans;
    }
};

最坏情况下每一次都要替换堆顶元素，因此时间复杂度为 O(NlogK)。可以看出使用堆的实现会使代码显得非常繁琐，因此一般使用优先队列编码：

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> ans;
        if (k == 0)  return ans;
        priority_queue<int> q;
        for (int i = 0; i < k; ++i) {
            q.push(arr[i]);
        }
        for (int i = k; i < arr.size(); ++i) {
            if (q.top() > arr[i]) {
                q.pop();
                q.push(arr[i]);
            }
        }
        for (int i = 0; i < k; ++i) {
            ans.push_back(q.top());
            q.pop();
        }
        return ans;
    }
};

当然由于 STL 的 priority_queue 内部实际上也是使用堆实现的，因此效率不如我们直接调用堆函数高。但使用起来更方便，更符合 STL 一般容器的常规用法。

数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

找的最大元素用小顶堆，算法同上，这次我们只需要输出堆顶元素即可：

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        priority_queue<int, vector<int>, greater<int>> q;
        for(int i = 0; i < nums.size(); ++i)
        {
            if(k > 0)
            {
                q.push(nums[i]);
                --k;
            }
            else
            {
                if(nums[i] >= q.top())
                {
                    q.pop();
                    q.push(nums[i]);
                }
            }
        }
        return q.top();
    }
};

数据流中的第 K 大元素

设计一个找到数据流中第 k 大元素的类（class）。注意是排序后的第 k 大元素，不是第 k 个不同的元素。

请实现 KthLargest 类：

KthLargest(int k, int[] nums) 使用整数 k 和整数流 nums 初始化对象。

int add(int val) 将 val 插入数据流 nums 后，返回当前数据流中第 k 大的元素。

我们使用优先队列直接解决：

class KthLargest {
public:
    priority_queue<int, vector<int>, greater<int>> q;
    int k;
    KthLargest(int k, vector<int>& nums) {
        this->k = k;
        for (auto& x: nums) {
            add(x);
        }
    }
    
    int add(int val) {
        q.push(val);
        if (q.size() > k) {
            q.pop();
        }
        return q.top();
    }
};

在上面的问题中我们都直接使用了 STL 提供的堆的实现，接下来借这道题，我们来自己手写一个堆的实现。

自己实现一个堆

首先根据之前学习的堆的基本知识我们知道，堆是一个完全二叉树，但是在编程语言中并不是用二叉树来实现堆的，而是用一个数组来实现。这是因为堆中父节点和子节点之间的编号是有一定的关系的：

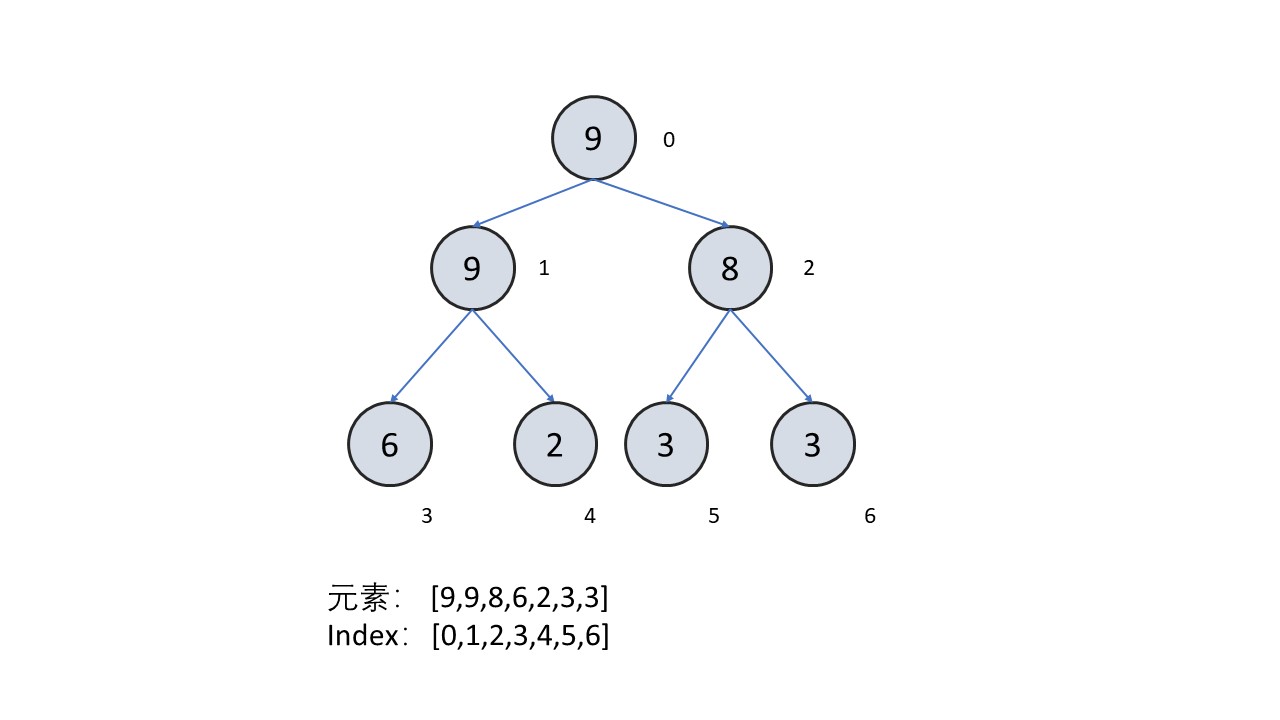
从上图可以看出堆中父节点和子节点的编号的关系：

已知一个节点编号 index ，它的父节点的编号为：

$$
index_{parent} = \lfloor \frac{index-1}{2} \rfloor
$$

已知一个节点编号 index ，它的左孩子节点的编号为：

$$
index_{leftchild} = 2 \times index + 1
$$

已知一个节点编号 index ，它的右孩子节点的编号为：

$$
index_{rightchild} = 2\times index + 2
$$

有了这个关系我们可以轻松的在一个数组中找到给定节点的父节点和孩子节点，接下来考虑如何实现堆的基本操作：插入和删除元素。

向堆中插入一个元素：我们只需要把该元素插入数组末尾，然后不停的向上调整该元素的位置直到符合堆的要求
在堆中删除一个元素：我们把当前堆顶和末尾元素交换，然后将新的堆顶元素向下调整位置直到符合堆的要求

具体的过程可以看手写堆实现动画，更方便理解。

因此为了达成上面的操作，我们需要写两个调整元素位置的函数，以及其他基本功能。

class Heap {
public:
    vector<int> heap;
    bool greater = 0;   //默认为大顶堆
    void BuildHeap(vector<int>& nums, int greater = 0)
    {
        this->greater = greater;
        for(int x : nums)
        {
            heap.push_back(x);
            AdjustUp(heap.size() - 1);
        }
    }
    
    int size()
    {
        return heap.size();
    }
    
    int top()
    {
        return heap[0];
    }

    bool compare(int i, int j)
    {
        return greater ? heap[i] < heap[j] : heap[i] > heap[j];
    }

    void swap(int i, int j)
    {
        int temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }
	// 向下调整节点
    void AdjustDown(int index)
    {
        //如果有孩子节点
        while(index * 2 + 1 < heap.size())
        {
            int largest = index;
            int leftchild = 2 * index + 1;
            int rightchild = 2 * index + 2;
            if(compare(leftchild, largest)) largest = leftchild;
            if(rightchild < heap.size() && compare(rightchild, largest)) largest = rightchild;
            if(largest == index) break; //如果当前根节点已经是当前子树最大或最小的节点则调整完毕
            swap(largest, index);
            index = largest;
        }
    }
	//向上调整节点
    void AdjustUp(int index)
    {    
        while(index)
        {
            int parent = (index - 1) / 2;
            if(compare(parent, index)) break;
            swap(index, parent);
            index = parent;
        }
    }
	//插入元素
    void push(int val)
    {
        heap.push_back(val);
        AdjustUp(heap.size() - 1);
    }
	//删除元素
    void pop()
    {
        swap(0, heap.size() - 1);
        heap.pop_back();
        AdjustDown(0);
    }
};

前 K 个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

哈希表统计频数即可，主要是学习C++优先队列如何自定义比较函数：

class Solution {
public: 
    struct cmp{
        bool operator() (pair<int, int>& x, pair<int, int>& y)
        {
            return x.second > y.second;
        }
    };
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int, int> map;
        for(int& x : nums)
        {
            ++map[x];
        }

        priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> q;
        for(auto& [num, count] : map)
        {
            if(q.size() == k)
            {
                if(count > q.top().second)
                {
                    q.pop();
                    q.push(pair(num, count));
                }
            }
            else q.push(pair(num, count));
        }
        vector<int> ans;
        while(!q.empty())
        {
            ans.push_back(q.top().first);
            q.pop();
        }
        return ans;
    }
};

上面是定义了一个结构体，在结构体中定义比较函数，构造优先队列时相当于传入函数对象。还可以用下面的方法：

static bool cmp(pair<int, int>& m, pair<int, int>& n) {
	return m.second > n.second;
}
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> q(cmp);

decltype 函数用于获取函数指针，传入的是函数的地址。