材质(Materials)
这一节开始学习图形学中材质的相关内容。我们之所以能看到现实世界中不同的物体有不同的材质,本质上就是因为不同材质对光线的吸收、反射、折射的能力不同,而描述这种能力的函数就是我们上一节中简单了解过的双向反射分布函数(BRDF),上一节中也说过,BRDF 就是材质,因此这一节讨论的内容实际上就是 BRDF。
双向反射分布函数(BRDF)描述反射的性质,那自然也存在双向折射分布函数(BTDF),他们统称为 BSDF,但一般来说 BRDF 也可以广义上代表折射或其他,因此也并没有严格的区分,说到 BRDF 就可以代表各种材质。
1 漫反射材质
漫反射是最简单的一种反射,但也算是最常见的,光线朝四面八方反射出去,如下图:
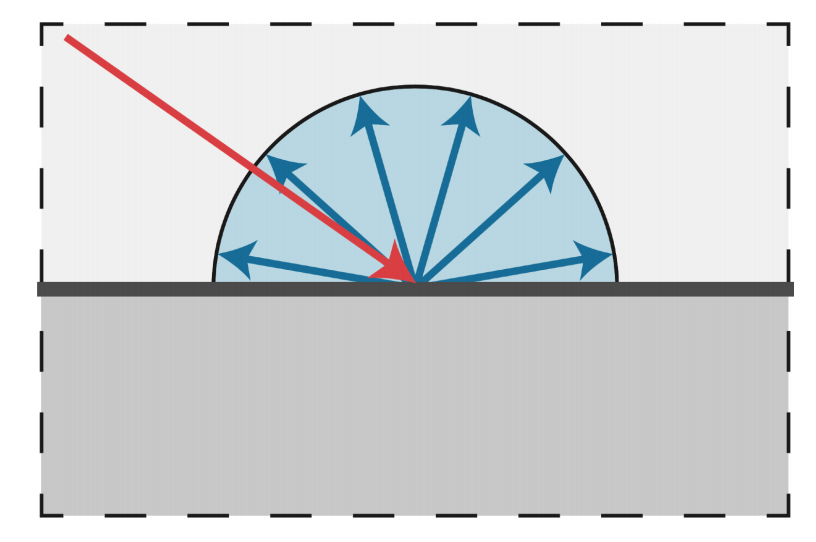
漫反射材质也是最简单的一种材质,是我们日常生活中经常见到的:

它的 BRDF 也非常简单,回顾布林冯光照模型中对漫反射的描述,其中漫反射系数当时我们理解为一个颜色,并且漫反射系数取值在 [0, 1] 之间,描述有多少光被反射了出去,那实际上漫反射系数的功能不就和 BRDF 一样吗,现在我们用之前学过的知识来推导漫反射系数到底是什么。
我们先考虑一个最简单的情况:
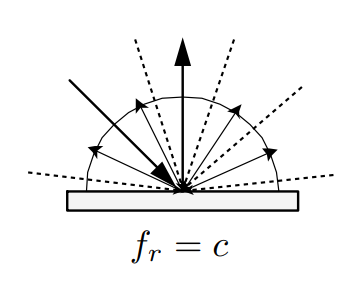
假设一个着色点的所有入射光,也就是各个方向入射的 Radiance 都是相等的,并且之前我们学过,漫反射与观察方向无关,也是均匀的向各个方向反射出去,也就是说各个方向出射的 Radiance 也是相等的。而 BRDF 是关于方向的函数,可漫反射又与方向无关,这说明漫反射的 BRDF 就是一个常数,只是一个系数用来描述入射进来的光有多少被反射出去。因此我们可以写出反射方程:
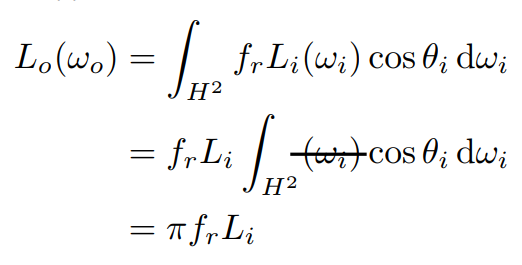
因为入射的 Radiance 都是相等的,所以 $L_i(\omega_i)$ 与 $\omega_i$ 无关,就可以统一写成一个常数 $L_i$,而 BRDF 也是常数,因此反射方程就是一个在半球面上关于函数 $cos\theta$ 的积分,积分结果就是 $\pi$,因此我们可以得到:反射出去的光 $L_o$ 就等于 $\pi f_r$ 倍的入射光 $L_i$ ,那么假设现在这个表面完全不吸收光,有多少入射就全部反射出去,那也就是 $L_o=L_i$ ,即 $\pi f_r=1$,因此这种情况下,漫反射的 BRDF 就是:
$$
f_r = \frac{1}{\pi}
$$
当然实际情况是表面一定会吸收一定的能量,因此漫反射的 BRDF 为:
$$
f_r = \frac{\rho}{\pi}, \ \rho \in [0,1]
$$
这样就描述了入射的光有多少被反射了出去,因此漫反射的 BRDF 的取值范围不是 $[0, 1]$,而是 $[0,\frac{1}{\pi}]$,当然 $\rho$ 也可以是一个三维向量,分别对应 [r, g, b] 分别反射多少。
2 Glossy 反射材质
Glossy 反射我们也很熟悉了,之前经常提到,上一节中也解释了 Glossy 反射是因为表面相对较为粗糙,以至于入射光不能完美的沿着镜面反射方向反射,而是沿着镜面反射方向一定范围内的区域反射出去,如下图:
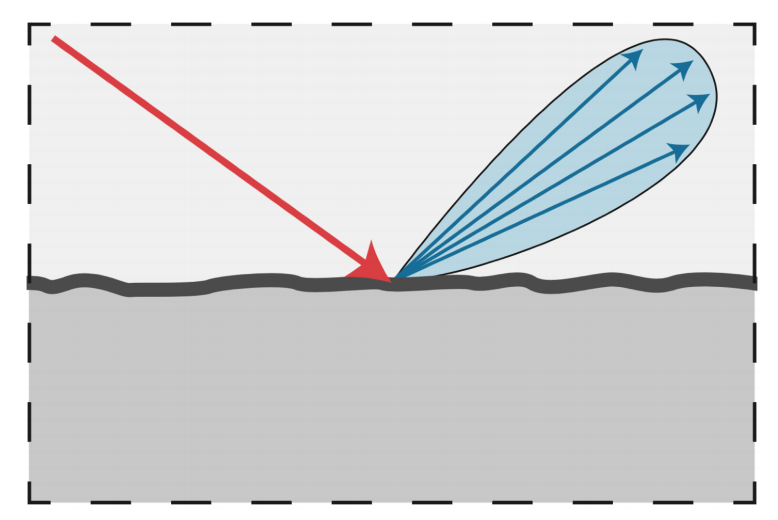
Glossy 材质的效果如下图:

3 折射材质
折射我们学过物理应该也很熟悉,类似水、玻璃之类的都是折射材质:
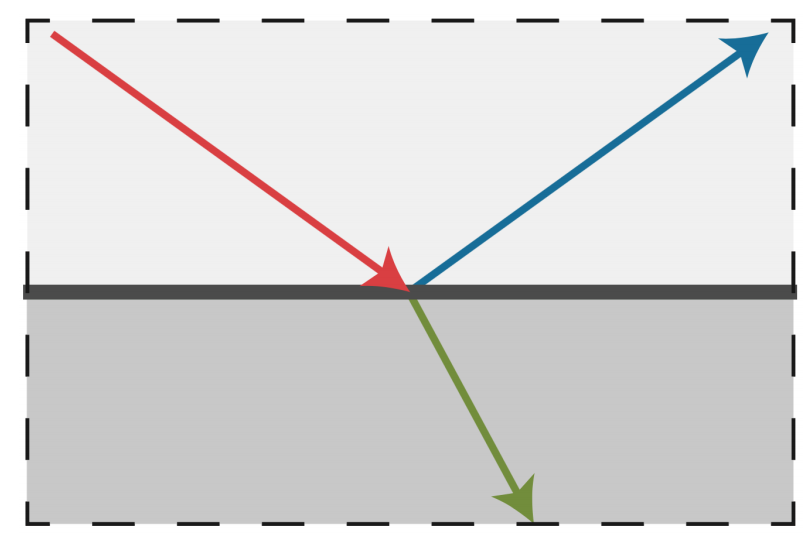
折射材质的效果:

左边是空气到水面,右边是空气到玻璃。折射材质表面的反射可以看成是完美的镜面反射,那么如何描述一个完美的镜面反射呢,我们知道空间中可以靠一个方位角 $\phi$ 和一个俯仰角 $\theta$ 来确定一个方向,那么描述完美镜面反射其实也就是描述入射光和反射光方向的关系。
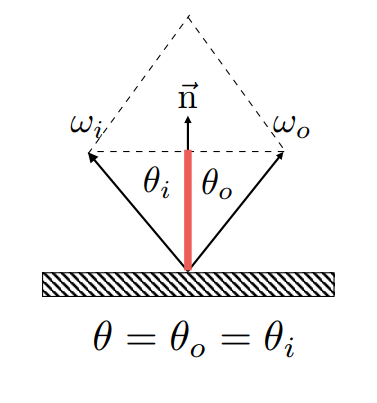
对于俯仰角,两条光线的俯仰角要一样,那也就是两个方向向量的和的长度刚好是图中红线的二倍:
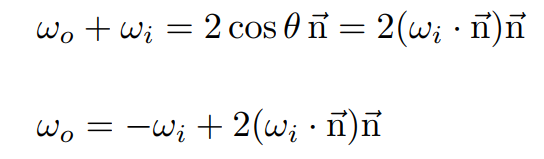
这样就得到用入射方向表示的出射方向了,对于一个完美镜面反射,只要知道了入射方向向量我们就可以算出出射方向。
对于方位角,就简单很多,如下图,是上面的场景的俯视图:

显然,只要两个方向共线即可。
接下来讨论折射,学过物理我们知道折射与折射率有关,因此折射的俯仰角和方位角的关系如下:
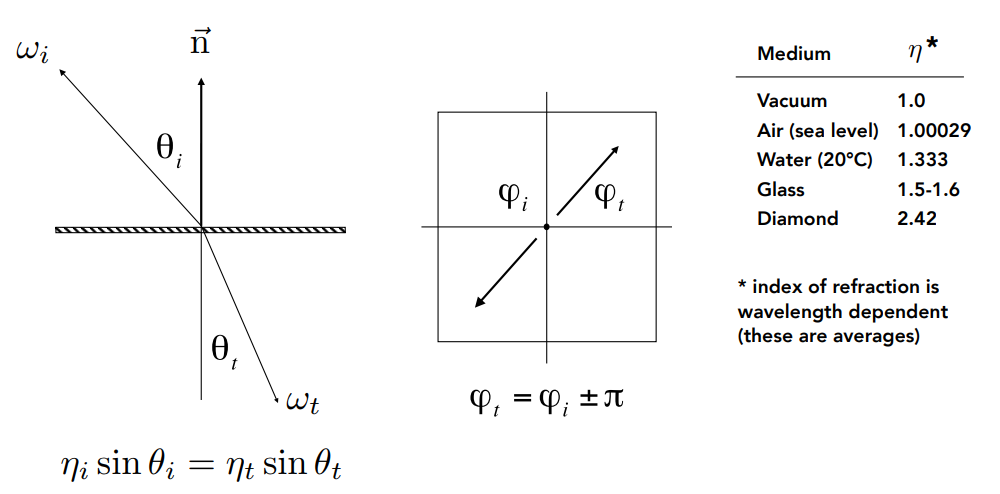
俯仰角满足入射光线与法线夹角乘以入射材质的折射率等于出射光线与法线夹角乘以出射材质的折射率,方位角关系和反射一样,右边还给出了常见材质的折射率。
于是根据这样的关系,知道了入射方向与法线的夹角,就可以得到出射方向与发现的夹角了,我们还可以稍微进行一下变形:
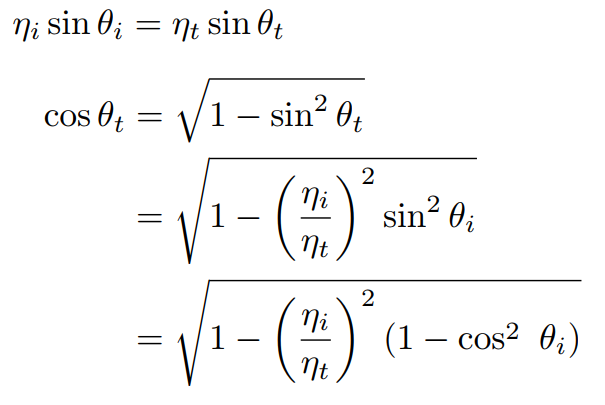
对于出射角 $\theta _t$ 来说,它的余弦必须是实数,而右边的根号可能会得到非实数,这样就没有意义,也就相当于折射不会发生,因此当根号下的数小于0 时,不会发生折射。而我们观察整个根号下的式子,要想小于0 ,就必须使得:
$$
(\frac{\eta_i}{\eta_t})^2(1-cos^2\theta_i) > 1
$$
显然 $(1-cos^2\theta_i)$ 不可能大于 1 ,因此只有当 $\frac{\eta_i}{\eta_t} > 1$ 时,不会发生折射,也就是入射材质的折射率大于出射材质的折射率时,折射可能不会发生,比如从水面向空气中传播的光线,就会有一部分不会发生折射:
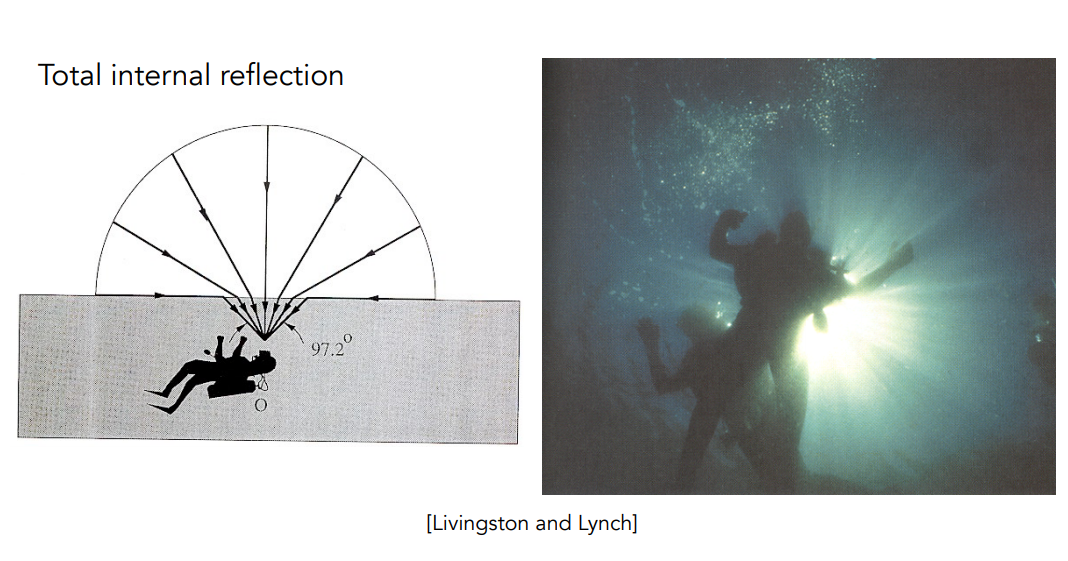
因此我们在水下看向水面永远只能看到一个锥形区域,而其它部分都是黑的。
4 菲涅尔项
生活中我们有很多现象与菲涅尔项描述的问题有关,比如:

我们从不同的视角看这本书,看到的书在桌面上的反射是不同的,这是因为最左边的图,我们视线的入射角大,因此观察到的反射就弱,而右边我们视线的入射角小,观察到的反射就强:
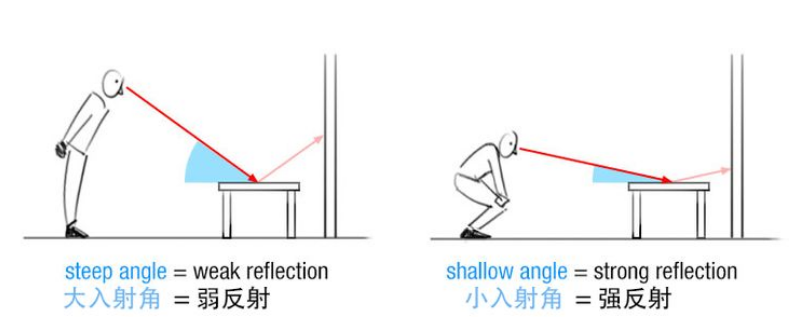
这就是菲涅尔项描述的东西。可以做一个简单的理解:菲涅尔效果就是在反射效果中,离你近的反射得更模糊,离你远的反射得更清晰。
当然从科学上解释就相对比较复杂了,目前只要知道菲涅尔项描述的是光在两种不同折射率的介质中传播时的反射和折射就可以了。
下图展示的是折射率为 1.5 的绝缘体的入射角和反射率之间的关系:
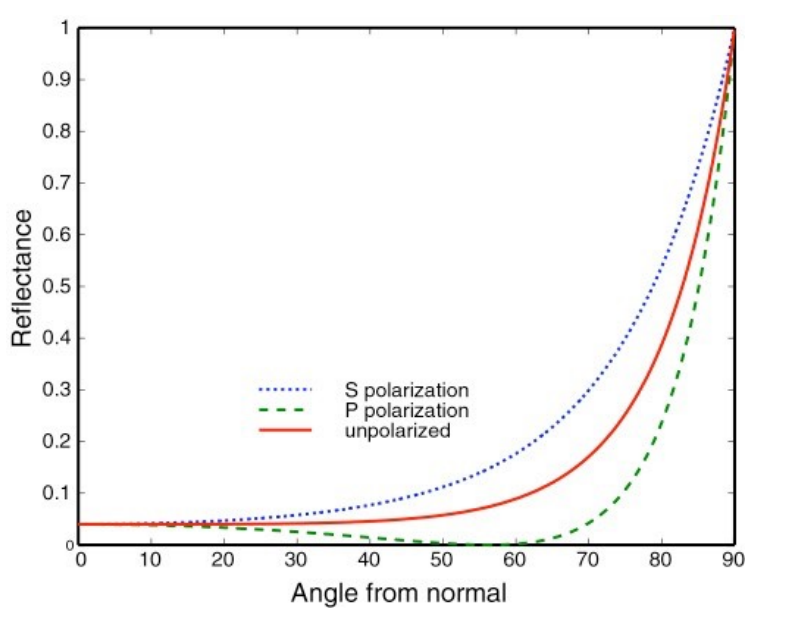
可以看到入射方向和法线夹角越大,相当于我们的观察角度越小,反射就越强。虚线代表极化后的光线的反射率,整体趋势是一样的。
下图是导体的反射率:
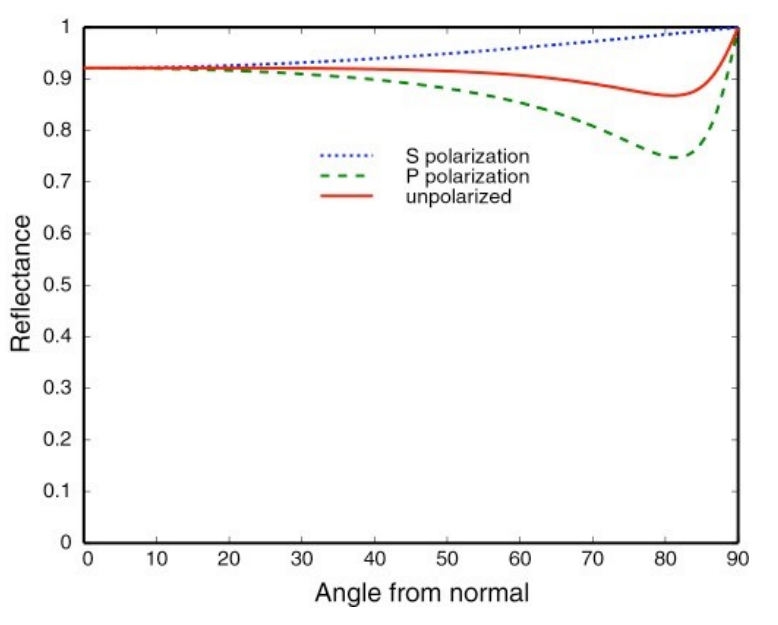
这说明导体无论从什么视角看,都可以看到相对明显的反射,比如金属之类的材质。
菲涅尔项的数学公式如下:

其中 $R_S$ 和 $R_P$ 是水平和垂直偏振光,也就是极化光的菲涅尔公式,我们在渲染中一般不考虑极化,因此取二者的平均即可。但是由于菲涅尔公式比较复杂,因此一般用 Schlick’s 近似来近似菲涅尔系数;
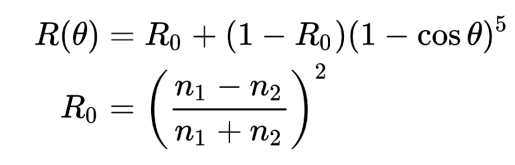
$R_0$ 是初始反射率,可以看到与两种材质的折射率有关, Schlick’s 近似显然会随着入射方向和法线夹角增大使得反射率从 $R_0$ 变为 1,和我们上面看到的图是差不多的,因此可以近似地表示菲涅尔项。
总体来说菲涅尔项描述的就是有多少光会发生反射,于是剩余的光就发生折射,在之后的渲染中我们也是用菲涅尔系数来混和计算得到的反射颜色和折射颜色的。
利用菲涅尔项还可以解释金属为什么几乎不会产生漫反射,因为金属的折射率是复数,对于金属来说, 由于金属内部是可以自由运动的电子,菲涅尔项表示反射的部分光,那么剩余的部分则是折射进金属内部被自由电子转化为其他形式的能量,相当于直接被金属吸收了,不会在内部发生次表面散射再从表面其他位置出去,因此也就几乎没有漫反射,而菲涅尔项表示的反射部分是高光反射,金属的菲涅尔项的基础反射率一般都代表了高光反射的颜色,也就体现为金属的颜色,例如金子的金色和铝的银色等。而对于非金属材质,高光反射颜色比较单一,并且会发生次表面散射,因此大部分被我们看到的是漫反射颜色。
5 微表面材质
微表面材质是现在应用极为广泛的材质,简单来说就是一个凹凸不平的表面在近处看可以看出凹凸的材质,但在远处看就只能看到一个光滑的镜面反射,这也符合我们生活中的物理事实,关键在于如何用 BRDF 来描述微表面材质。
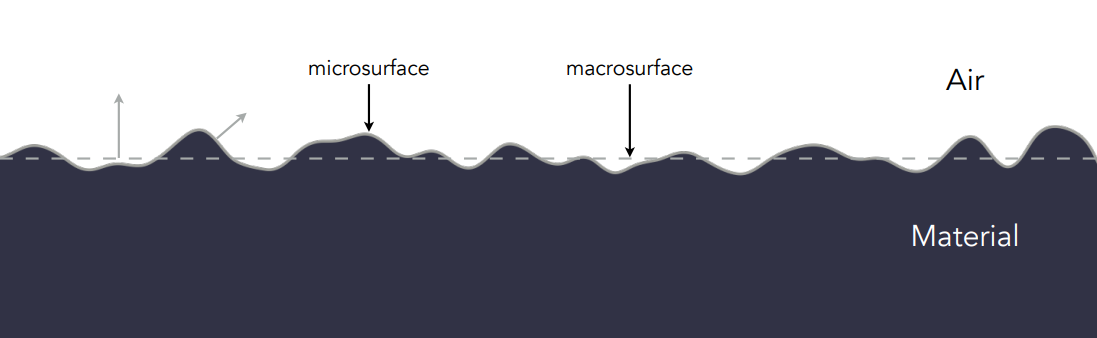
上面的图实际上已经体现了微表面材质的一个核心思想,就是凹凸不平的表面的每一个微表面的法线方向会有明显的不同,如下图:
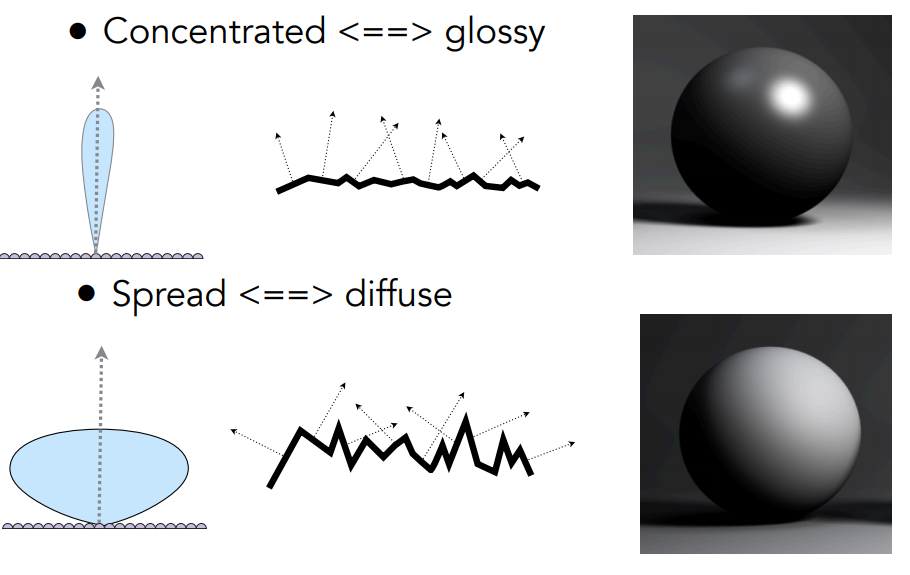
对于一个相对平滑的表面,它的各个微表面的法线方向会集中在一个范围内,但是对于一个粗糙的表面,它的各个微表面的法线方向分布会较为分散,因此描述微表面的 BRDF 的一个关键就是法线分布。微表面的 BRDF 写成如下形式:
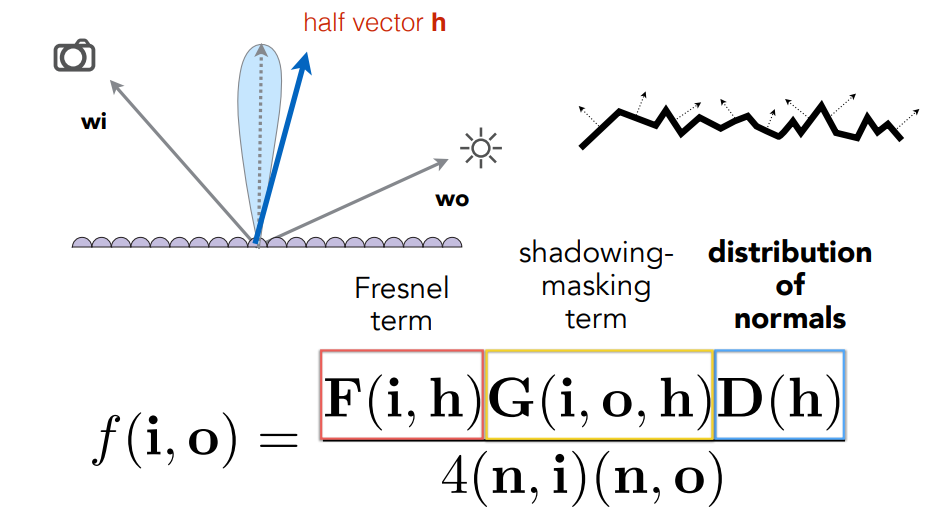
其中 D 是法线分布函数,表示有多少微表面会被看到,只有微表面的法线方向在光线入射方向和观察方向的半程向量方向才会被看到,如下图 (a) ;G 是阴影项,因为微表面凹凸不平,那么当入射光线贴着表面入射时,表面上就会有一部分微表面被其他微表面遮挡住而产生阴影,类似于我们之前说的环境光遮蔽,G 就是用来描述法线方向是半程向量的微表面中有多少微表面会因为互相遮挡而不被看到; F 是菲涅尔项,表示这些微表面有多少光会被反射,如下图 (b) 和 (c):
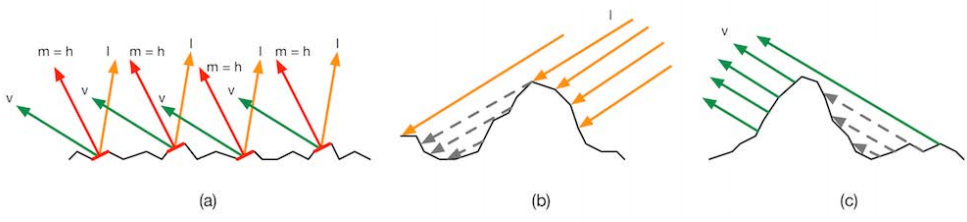
G 就是用来描述物体表面本身的遮挡的。
微表面非常强大,下面是一些利用微表面材质渲染的效果:

可以看到表面镌刻、尼龙等细节表现得很好,而这些物体当我们离远看的时候自然不会有这样的细节,表现出的就是正常的镜面反射。
6 各向同性和各向异性材质
我们生活中还有一些现象,比如:

铝合金锅底的这种放射的纹路,再比如电梯间的光会呈现出拉线的形状:

仔细观察这些现象,是因为材质表面具有一定的方向性,比如上图中的电梯间的金属,明显是有竖直方向的磨砂纹路的,这样的材质就称为各向异性材质,而我们正常见到的材质被称为各向同性材质。

可以看到各向同性材质的表面上每个点的法线方向分布是均匀的,而各向异性材质表面的法线分布是明显具有方向性的。
体现到 BRDF 上,各向同性材质的 BRDF 只与入射方向和出射方向的相对位置有关,也就是只要两个方向的相对位置不变,无论这两条线怎么旋转,BRDF 都是一样的;而各项异性材质的 BRDF 还与入射方向和出射方向的绝对位置有关,即使二者的相对位置不变,但是绝对位置发生变化,也会影响反射效果,即各向异性材质的 BRDF 满足:
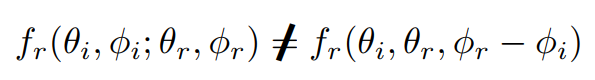
生活中还有很多各向异性材质,比如天鹅绒:

再比如尼龙材质:

还有刚才说到的金属锅、水壶之类的:

7 总结 BRDF 的性质
我们见过了这么多 BRDF ,现在来总结一下 BRDF 的性质:
- 首先是非负性,这是一定的,因为能量是守恒的,反射出去的能量只能变小或者不变,不可能反射出更多的能量:
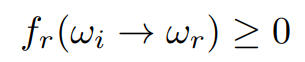
- 线性,BRDF 可线性累加
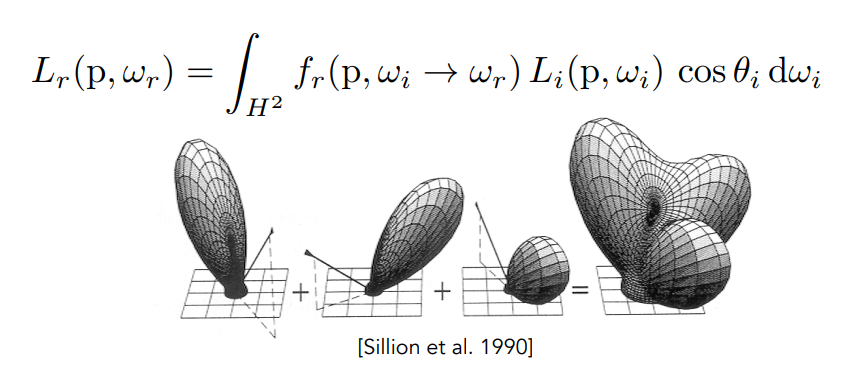
- 双向性, BRDF 的名字就叫双向反射分布函数,说明入射方向和出射方向可以对调,也满足同一个 BRDF
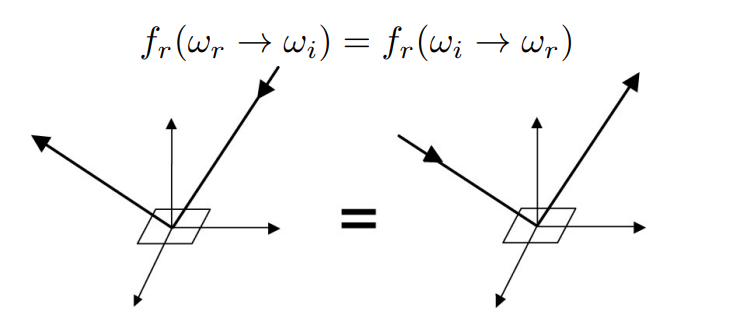
- 能量守恒,同样是刚才说过的,反射出的能量不可能变多,最多也就是和入射的能量一样
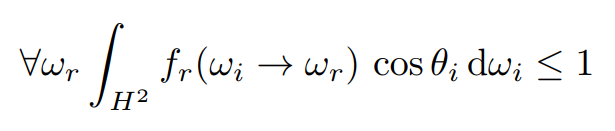
8 测量BRDF
所谓测量 BRDF 是因为材质的反射性质很多时候由我们直接去定义一个函数一定是不够准确的,因此很多时候需要我们实际去测量某一种材质的 BRDF,然后再利用测量的准确值去帮助渲染。
要测量 BRDF 我们只需要知道入射方向、出射方向,和这两个方向上的 Radiance 就可以得到,这些值都可以借助仪器直接测量出来,因此我们只要固定光源,然后移动相机就可以得到一个入射方向上所有出射方向的 BRDF ,如下图:
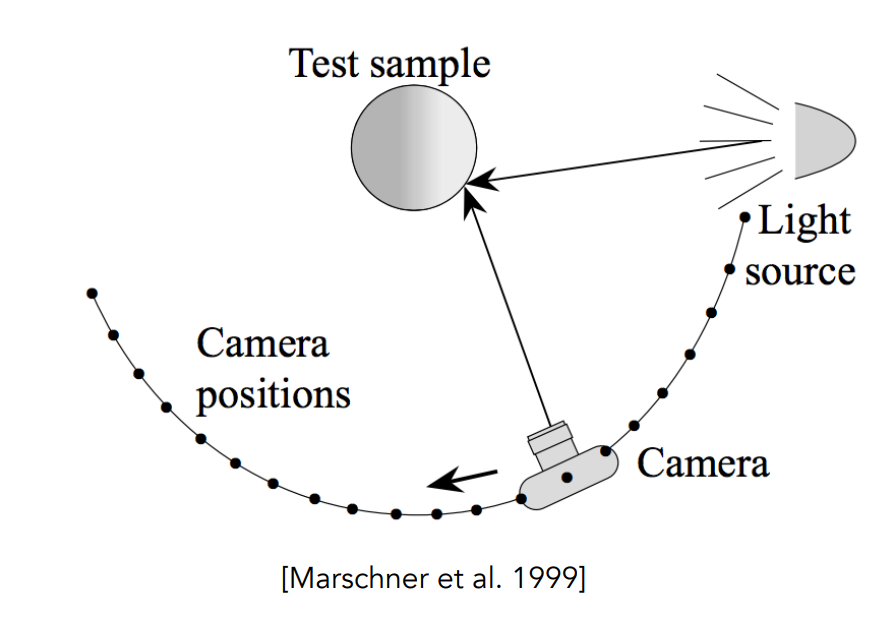
然后再把所有光源位置也都测一遍,就得到了整个材质的 BRDF,下图是一个测量 BRDF 的仪器:

但是我们知道 BRDF 是四维的,因为它表示的是两个三维空间方向之间的关系,每一个三维空间方向可以用一个方位角和一个俯仰角表示,所以 BRDF 有四个维度,这对于测量来说,要测量的数据量会非常庞大,并且怎么样存储这些 BRDF 值也是一个巨大的挑战。
但我们上面刚刚学习过,各向同性 BRDF 满足:
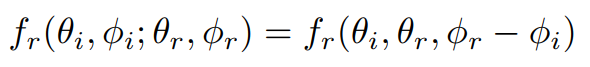
因此,只要知道了两个方向的相对角度,就可以确定 BRDF,所以,原本四维的 BRDF 如果是各向同性的,就可以变为三维:
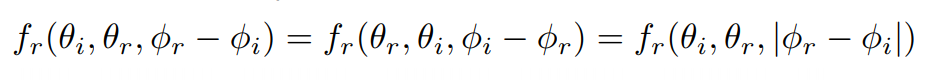
减少了一个维度,这会使 BRDF 的测量数据量大幅减少。至于如何存储又是另一个专门研究的领域,各种压缩算法,这里不再讨论。
MERL BRDF 数据库很早之前就测量了各种各向同性材质的 BRDF(可能现在还补充了大量各向异性材质),因此我们现在需要不同材质的 BRDF 可以直接利用这些测量好的数据,而无需考虑复杂的测量和存储方式是如何实现的:
