【计算机图形学】（十三）路径追踪

路径追踪（Path Tracing）

这一节我们正式开始学习路径追踪技术，首先我们要利用上一节的辐射度量学基础理解双向反射分布函数并推导出反射方程和渲染方程，然后利用渲染方程理解全局光照，之后简单复习一下蒙特卡洛积分的相关内容，最后通过解渲染方程来构建路径追踪算法。这一节内容可能非常硬核，涉及物理、微积分、概率论等多方面的知识，但这也是迈向真正的现代图形学大门的第一步。

1 双向反射分布函数（BRDF）

在学习路径追踪之前我们还需要一系列的前置知识，第一个就从双向反射分布函数（Bidirectional Reflectance Distribution Function）开始。

我们假设一个平面 dA 从某个方向 $\omega_i$ 接收到的 Radiance 会被转化成这个平面上的能量 $E(\omega_i)$ ，然后这些能量又会从 dA 向四面八方反射出去，但一般情况下不会全部反射出去，而是会有一部分能量被保留，另外的能量被反射出去，假设在某个方向 $\omega_r$ 反射出去的能量是 $L_r(\omega_r)$，那么在平面 dA 从方向 $\omega_i$ 接收到的能量 $E(\omega_i)$ 中有多少能量会被反射到 $\omega_r$ 方向成为 $L_r(\omega_r)$，这二者之间存在一个关系，这个关系就叫做双向反射分布函数。

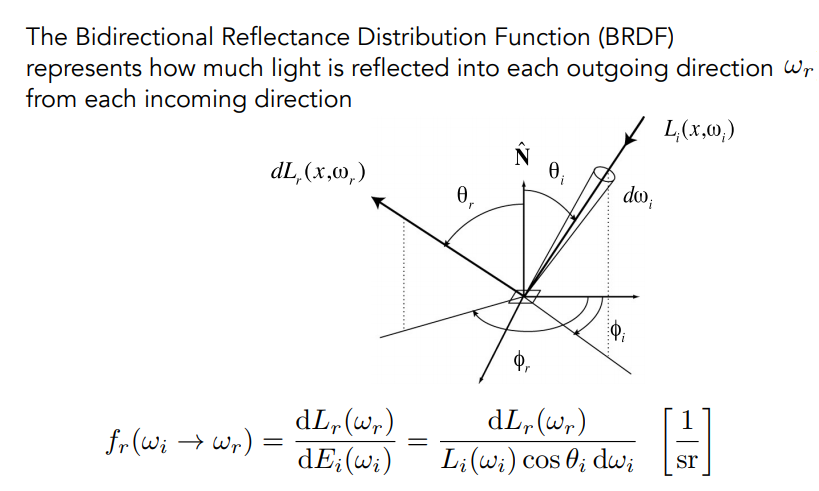
可以看到 BRDF 就是 $L_r(\omega_r)$ 和 $E(\omega_i)$ 的比值，它描述的就是一个平面从某个方向接收到的能量会往另外某个方向反射多少。

从物理意义上来说， BRDF 描述的其实就是物体表面的材质属性，物体之所以在我们看来会显示出不同的材质，就是因为它的表面对光的吸收能力不同，反射能力不同，BRDF 描述的正是一个表面的这种反射光的能力，因此我们说 BRDF 本质上表示的是表面的材质。

2 反射方程

有了 BRDF，现在我们考虑一个着色点 $p$，回顾上一节最后我们说的 Radiance 和 Irradiance 的联系，$p$ 点的 Irradiance 就是 Radiance 在各个方向上的积分，那么现在我们从一个方向 $\omega_r$ 去观察点 $p$，也就相当于去计算 $p$ 点从各个方向接收到的能量在 $\omega_r$ 方向总共能反射出多少，那不就是点 $p$ 从每个方向 $\omega_i$ 接收到的能量 $L_i(p,\omega_i)$ 乘以 $\omega_i$ 方向到 $\omega_r$ 方向的 BRDF 再全部积分起来就可以了吗。

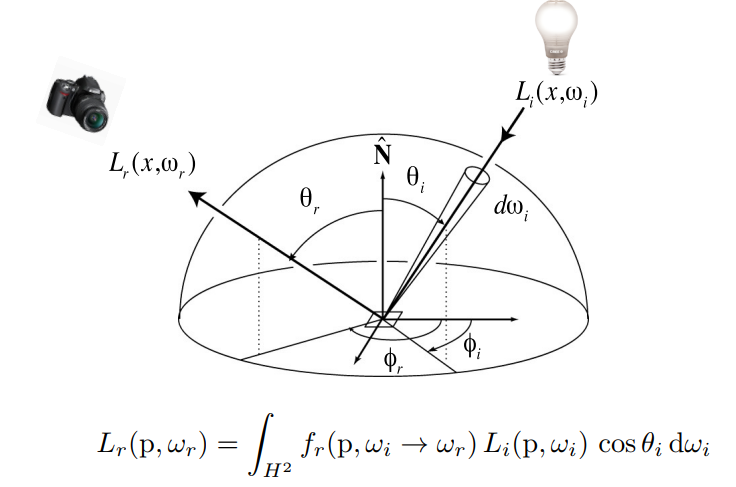
上面的公式表达的意思就是刚才说的，点 $p$ 从每个方向 $\omega_i$ 接收到的能量 $L_i(p,\omega_i)$ 乘以 $\omega_i$ 方向到 $\omega_r$ 方向的 BRDF 再全部积分起来，就得到了一个着色点从四面八方接收到的能量往观察方向反射了多少。这个公式就叫做反射方程。

3 渲染方程

反射方程计算的是一个表面从外界接收到的光，能被我们看到多少，如果这个物体本身就会发光呢？那它本身也会向我们的观察方向 $\omega_r$ 发出能量，因此我们可以在反射方程上加上一个自发光项 $L_e(p,\omega_o)$：

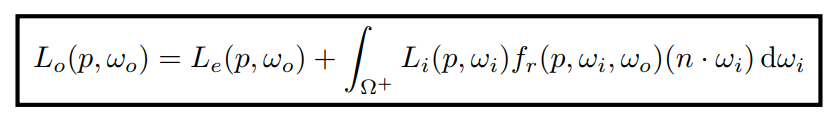
这样就得到了能描述更一般情况的渲染方程，上式中 $L_o(p,\omega_o)$ 就是 $p$ 点在 $\omega_o$ 方向反射出的总能量， $L_e(p,\omega_o)$ 是 $p$ 点自身在 $\omega_o$ 方向放射出的能量，球面积分就是 $p$ 点从四面八方接收到的光反射到 $\omega_o$ 方向的总能量，$\Omega^+$代表上半球面，$f_r(p,\omega_i,\omega_o)$ 表示点 $p$ 从 $\omega_i$ 方向到 $\omega_o$ 方向的 BRDF，这里的余弦同样用向量点乘表示，因为所有这些向量也都是指示方向的单位向量，并且都是和布林冯模型中一样，从点 $p$ 指向外边的。

4 全局光照

渲染方程就可以描述我们之前经常说到的全局光照，这也是光栅化不好去解决的问题（不代表不能解决），因为光栅化中光线只弹射一次，而全局光照正是因为光线会弹射很多次使得本来光线达到不了的地方能被照亮。

接下来我们就从简单情况开始，理解渲染方程为什么能表示全局光照。首先考虑只有一个点光源的情况，也是之前我们讨论的最多的情况：

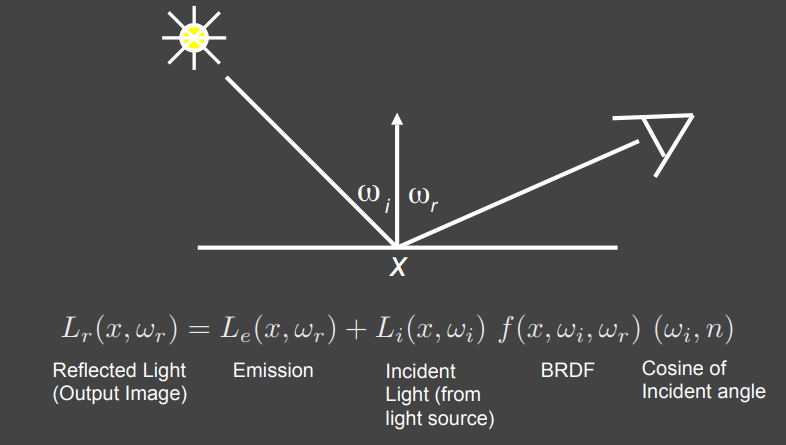
这时的渲染方程就可以写成上面的形式，相当于只有一个方向有入射的 Radiance ，那如果现在有多个点光源：

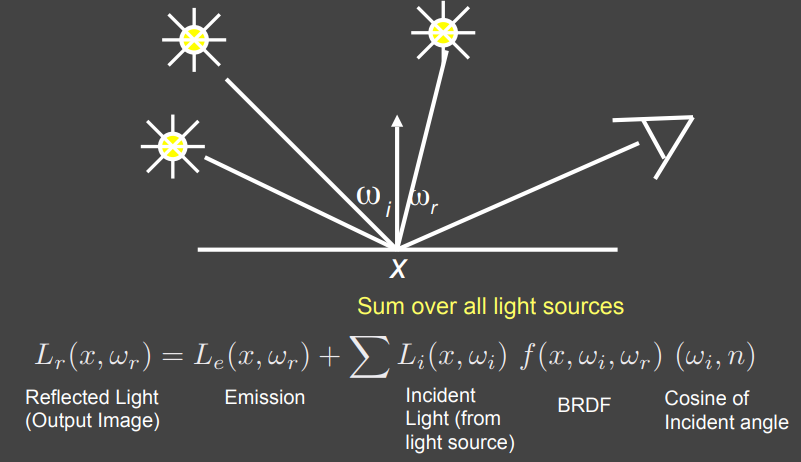
渲染方程也很简单，就是把全部的点光源反射加起来。接下来如果点光源变成了面光源，相当于从离散到连续：

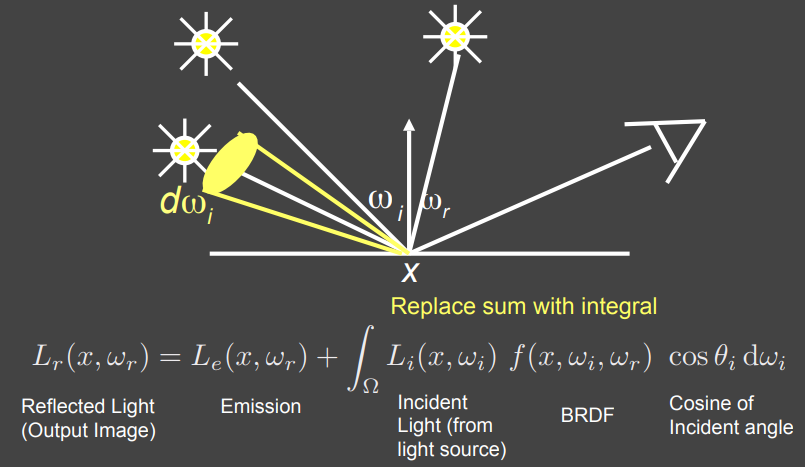
我们也能理解，离散的求和就是连续的积分，这也是我们刚才得到的最一般的渲染方程。

到此为止我们讨论的都是光源照射到物体上，也就是直接光照的情况，那对于一个物体表面，他接收到的光不全是从光源来的，还可能是从其他物体表面反射出来的光：

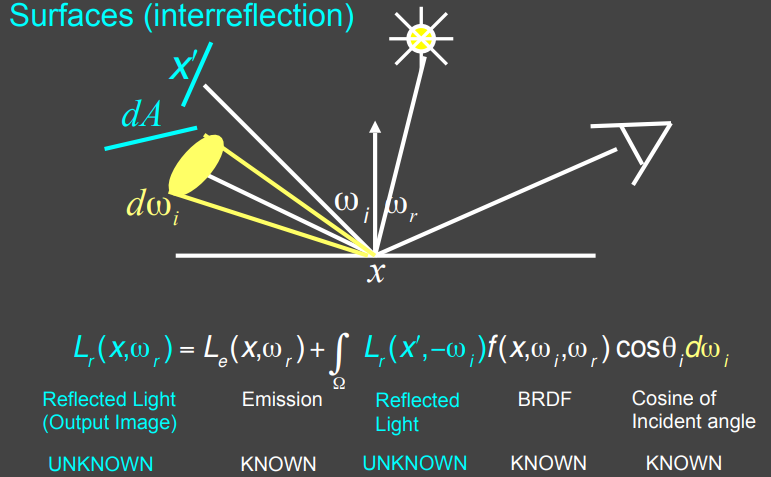
比如上图中的 $X’$ 是其他物体的表面，反射出的光同样会被我们的观察点接收到，这时着色点 $x$ 接收到的从平面 $X’$ 反射来的光相当于我们从点 $x$ 沿着 $-\omega_i$ 方向观察平面 $X’$ 得到的结果，因此着色点 $x$ 接收到的从平面 $X’$ 反射来的光就是上面式子中的 $L_r(X’,-\omega_i)$，从这个渲染方程我们可以看出整个过程是一个递归的过程，当前物体反射的光不仅取决于光源，还取决于其他物体反射的光，其他物体反射的光又取决于光源和别的物体，这也正是渲染方程能够表示全局光照的原因。

我们继续观察上面的渲染方程，我们要求解的未知数也包含在积分中，所以这是一个积分方程，并且这个看似复杂的积分方程实际上是一个经典的积分方程，叫做弗雷德霍姆积分方程（Fredholm Integral Equation），这个方程可以简化的写成如下形式：

这满足第二类弗雷德霍姆积分方程的一般形式，其中 $K(u,v)dv$ 被称为光线传播算子，表示的是光线 $l(v)$ 经过光线传播算子就传播到了 光线 $l(u)$ 上，这和我们之前说的一个点吸收的光再反射出去的概念其实是一样的。

接下来我们再进一步简化，把这个方程写成矩阵形式：

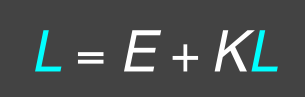
至于积分怎么写成矩阵形式，这里不展开讨论，这对我们来说也不重要，总之写成这样的形式之后，我们就可以进一步操作，移项之后再左乘对应的逆矩阵：

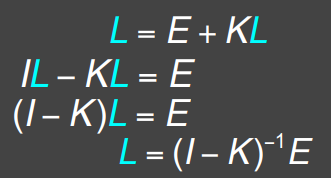
然后根据二项式定理，对于矩阵也存在类似泰勒展开的形式， $(I-K)^{-1}$ 的泰勒展开就类似于 $\frac{1}{1-x}$ 的泰勒展开，于是上式可以写成：

我们把这个式子展开进行分析：

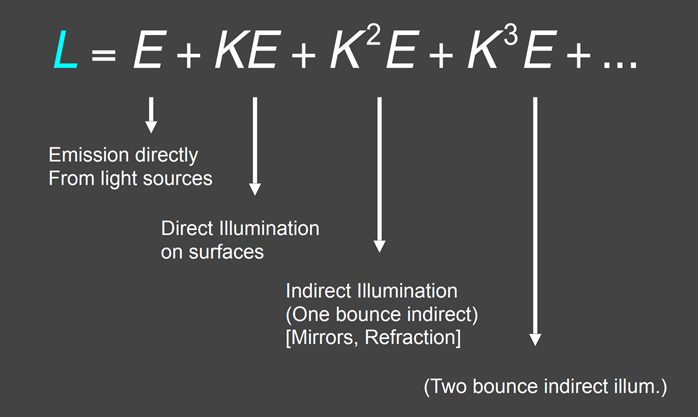
先明确这里面各个字母代表什么，在他们没变成这样之前，$L$ 是各个平面反射出的光（可能是我们观察的平面，也可能是其他平面），$E$ 是来自于光源的光，$K$ 是光线传播算子，所以直接来自于光源的光 $E$ 每乘一次光线传播算子 $K$ 就代表光线弹射了一次，所以 $KE$ 表示直接光照，也就是光线只在观察表面弹射了一次进入我们的眼睛，$K^nE$ 表示在多个表面弹射了 n 次之后进入我们的眼睛，我们观察到的光是所有这些光线的总和。

换句话说，渲染方程表示：我们看到的光是直接来自于光源的光和经过若干次反射后达到我们眼睛的光的总和。这显然是符合物理世界本身的规律的。而之前的光栅化着色过程，相当于只有前两项：

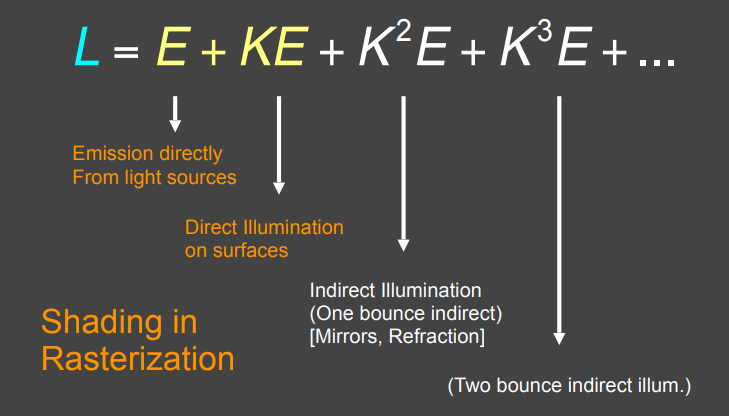
因此渲染方程可以表示全局光照，因为它考虑了整个场景中经过若干次弹射的光线。

下图是只有直接光照渲染出来的图：

可以看到因为只计算了直接光照，也就是光线只弹射一次，所以没有光线直接照射到的地方，比如点 $p$ 就是全黑的。下面是计算了一次全局光照渲染出来的图，一次全局光照是指光线额外弹射了一次：

点 $p$ 可以被看到了，但是注意房顶上的吊灯，此时它还是黑色的，下面是计算了四次全局光照的效果：

点 $p$ 变得更清晰了更亮了，而且房顶上的吊灯也变得透明了，因为它是玻璃材质，透射的光进入它的内部在只计算一次额外弹射的情况下是无法被反射出去被我们看到的，所以经过多次弹射后就会显示出来，这也是合理的。下面是计算了十六次全局光照的效果：

可以看到整个画面已经没有太大的变化了，这说明光线弹射的次数越多并不会使画面越亮，而是会逐渐收敛到一个状态，因为光线弹射的越多能量衰减的也越多，这也是和现实世界完全一致的，因此整个渲染方程非常科学的描述了整个场景中光线的传播，所以用渲染方程渲染出的画面自然也就更加接近真实世界。

5 蒙特卡洛积分

彻底理解了渲染方程之后，我们就要开始用渲染方程构建图像渲染算法了，但对于我们编码来说，只有这个渲染方程是不够的，因为我们要能够解出这个方程，得到一个计算便捷的表达式，才能去写代码，而我们知道计算机解方程使用的是数值的方法，尤其是对于这样复杂的积分方程，所以我们先简单复习一下计算定积分的常用数值方法——蒙特卡洛积分。

一般来说计算定积分，我们会先把不定积分算出来，然后再把区间端点代入相减就得到了区间上的定积分，但是对于形态比较复杂的函数来说，我们不容易求出它的不定积分，如下图：

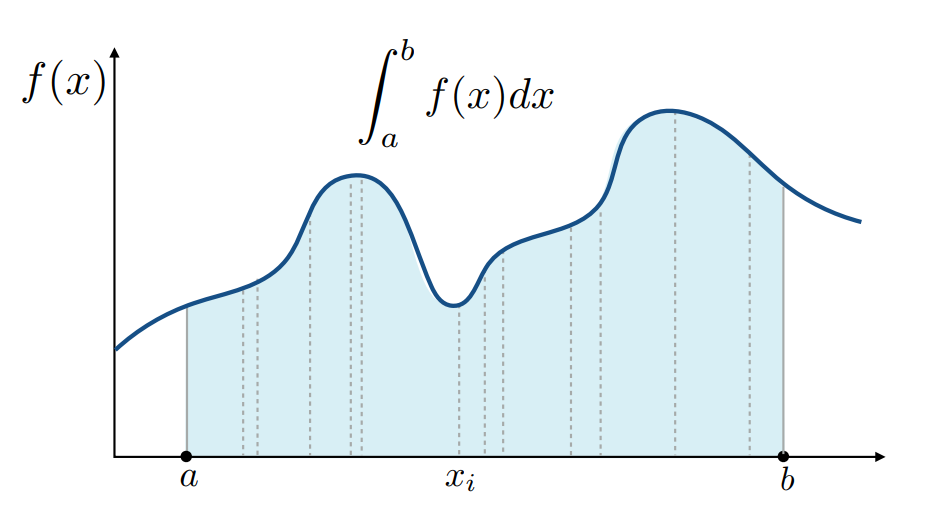
这时就要用数值方法去求积分了，我们知道积分就是面积，经典的黎曼积分就是在区间内取无数个小的长条把他们的面积加起来，而蒙特卡洛积分则是结合了概率论的方法，在区间 $(a,b)$ 内以某种概率分布随机的取一个点，把这个点的函数值作为矩形的高，然后区间长度作为矩形的宽，求出一个矩形面积，随着采样次数增多，把所有的矩形面积取平均就得到了整个区间的近似积分，采样点越多，结果自然也就越接近真实结果。

所以假设我们要计算定积分：
$$
\int_{a}^{b}f(x)dx
$$
我们以一个概率分布 $p(x)$ 在区间 $(a,b)$ 内随机的选取采样点 $X_i$，概率论告诉我们 $p(x)$ 叫做概率密度函数（pdf），则该定积分的蒙特卡洛估计为：
$$
F_N = \frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)},\ X_i \sim p(x)
$$
以均匀分布为例，区间 $(a,b)$ 上的均匀分布的概率密度函数就是：
$$
X_i \sim p(x) = \frac{1}{b-a}
$$
于是利用均匀分布采样的蒙特卡洛估计为：
$$
F_N = \frac{b-a}{N}\sum_{i=1}^{N}f(X_i)
$$

6 路径追踪

有了前面所有的前置知识，现在我们来正式学习路径追踪。学习一个方法的时候，要学习的第一件事就是为什么要学习这个方法？

我们之前学习 Whitted 风格光线追踪是为了解决光栅化渲染中的不足，所以路径追踪自然是为了解决 Whitted 风格光线追踪的不足。现在来回顾 Whitted 风格光线追踪有哪些问题。

首先，在一开始学习 Whitted 风格光线追踪时我们就假设了，所有光线的反射都是完美的镜面反射，也就是只沿着镜面反射方向传播，这显然是不合理的，比如我们之前也提到过的 Glossy 反射：

不过之前我们没有说 Glossy 反射为什么会呈现出这样的效果，这就是因为它的表面没有那么光滑，不足以使光线完美的沿着镜面反射方向传播，而是使光线在镜面反射方向附近一定范围内散射出去，所以呈现出来就是这样模糊的效果。因此 Whitted 风格光线追踪不好处理 Glossy 反射。

其次，光线遇到漫反射就会停下来。在之前的布林冯光照模型中，只有直接光照会使物体表面显示出颜色，而且这个颜色在之后的传播中也不会继续传播，所以相当于光线遇到漫反射就不再弹射了，如下图：

这是一个只有漫反射的场景，左图是只有直接光照的效果，所以天花板没有光源直接照射就是黑的，并且长的立方体左表面也是黑的；而右图是全局光照的效果，可以看到长的立方体左表面是红色的，这是因为左边的墙是红色的，显然右边的图更接近真实场景，这个真实场景也是存在的，后面我们会看到。

综上， Whitted 风格光线追踪实际上是错误的，因为它并不符合现实世界的物理规律，而之前我们推导的渲染方程是绝对符合物理规律的正确的光线计算方式。而要使用渲染方程来渲染图像，就要解方程，接下来我们从最简单的情况来分析如何求解渲染方程。

先考虑只有直接光照的情况，我们只考虑一个着色点，场景中只有一个面光源，如下图：

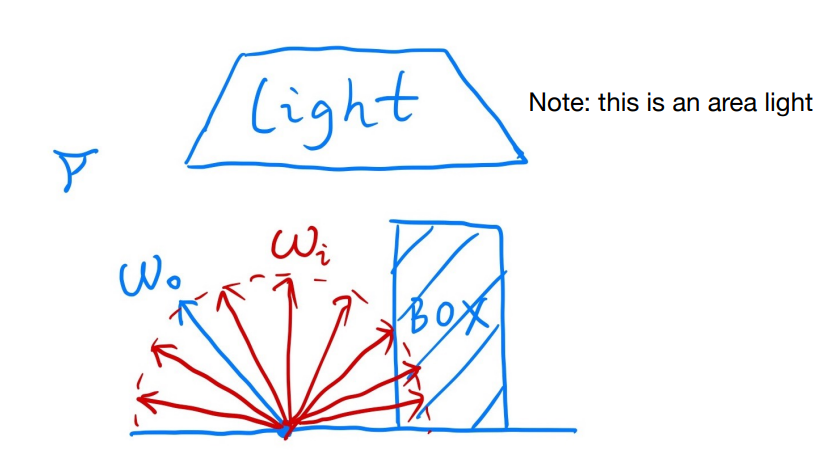
我们的观察方向是 $\omega_o$，不考虑着色点本身发射的光，于是可以得到一个渲染方程：

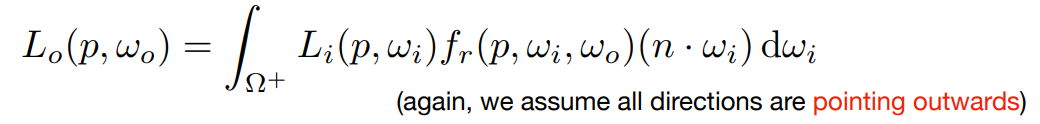
现在用蒙特卡洛积分来解这个方程，回顾蒙特卡洛估计的一般形式：
$$
F_N = \frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)},\ X_i \sim p(x)
$$
我们只要知道被积函数 $f(x)$ 和概率密度函数 $p(x)$ 就可以了，在这里被积函数 $f(x)$ 显然就是：

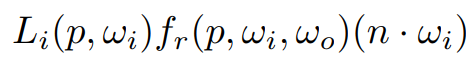
概率密度函数 $p(x)$ 我们就取均匀分布，但现在是一个半球面上的积分，半球面的均匀分布自然是：

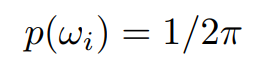
于是我们的渲染方程就可以写成：

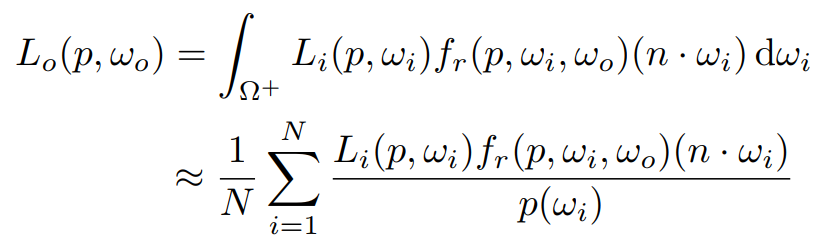
我们把积分转化成了求和的形式，这意味着我们可以写代码了，根据这个求和表达式，就能写出一个计算着色的算法：

shade(p, wo)
    Randomly choose N directions wi~pdf		//随机的选择N个方向，服从某个概率密度函数pdf的分布，这里是均匀分布
    Lo = 0.0
    For each wi		
        Trace a ray r(p, wi) 		//对每一个方向从着色点打出一条光线
        If ray r hit the light		//如果这个光线能到达光源，就按照公式计算着色
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi) 
    Return Lo

OK，现在我们考虑更复杂一点的情况，如果场景中有其他物体，那么公式中的来自各个方向的光就不一定是来自于光源了，也就是说我们从着色点打出一条光线可能不是达到光源，而是到达其他物体表面：

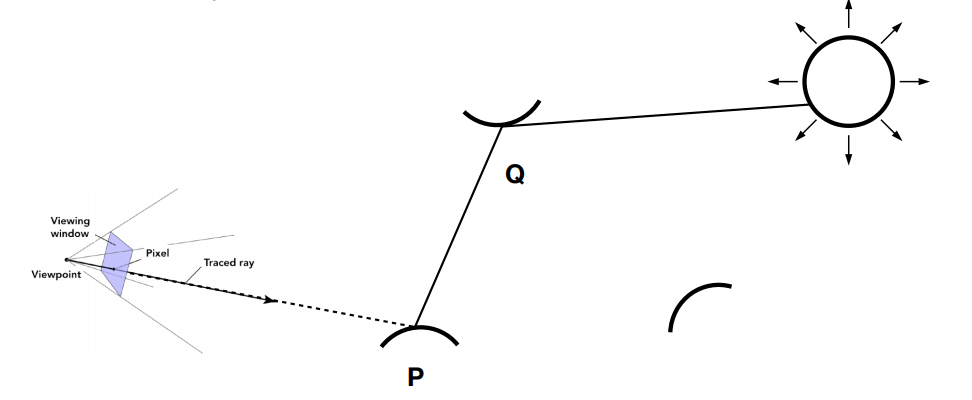
这时就按我们之前的递归做法，把着色点 P 当成观察点，然后计算 Q 点的着色，所以我们的代码只要加上另一个 if 判断：

shade(p, wo)
    Randomly choose N directions wi~pdf		//随机的选择N个方向，服从某个概率密度函数pdf的分布，这里是均匀分布
    Lo = 0.0
    For each wi		
        Trace a ray r(p, wi) 		//对每一个方向从着色点打出一条光线
        If ray r hit the light		//如果这个光线能到达光源，就按照公式计算着色
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi) 
        Else If ray r hit an object at q	//如果达到了其他物体表面，就递归地计算
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi)
    Return Lo

这样似乎就完成了一个像素的着色，但这样可以吗？一定是不行的，因为这样去追踪光线会导致计算量爆炸，下面的图说明了这种情况：

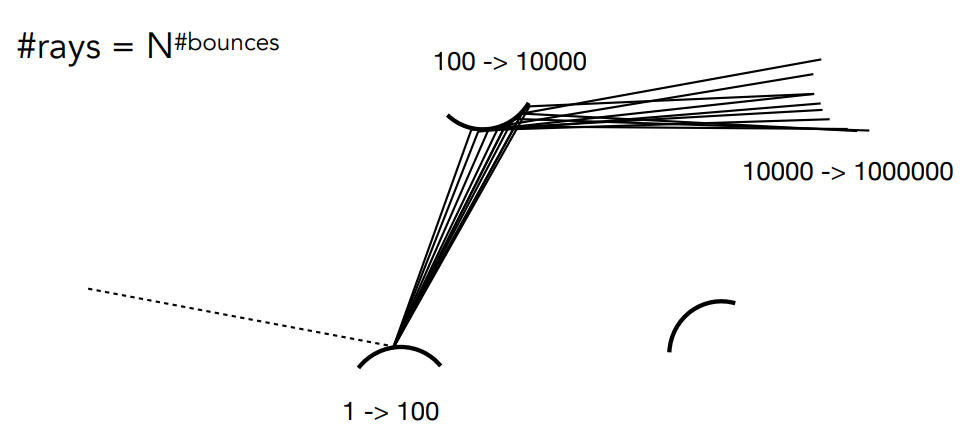
假设我们每次随机采样就选了 100 个方向，那么我们就要追踪 100 条光线，每一条光线如果打到其他物体表面又会采样出 100 条光线，这样经过两次弹射我们就要追踪 100 万条光线，这显然是不能接受的，因此我们就要考虑怎么样才能不让光线数量爆炸，因为这是呈指数增长的，所以只有当光线数量为 1 的时候，不管怎么弹射，它都还是一条光线。于是我们就随机采样一条光线，只跟踪这一条光线，那循环也不需要了，我们的代码就可以简化为：

shade(p, wo)
    Randomly choose 1 direction wi~pdf		//随机的选择1个方向	
    Trace a ray r(p, wi) 		//从这个方向打出一条光线
    If ray r hit the light		//如果这个光线能到达光源，就按照公式计算着色
        Lo += (1 / N) * L_i * f_r * cosine / pdf(wi) 
    Else If ray r hit an object at q	//如果达到了其他物体表面，就递归地计算
        Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi)
    Return Lo

上面的代码就是路径追踪的基本思路，只跟踪一条光线，就叫做路径追踪。

显然，这样的方法计算出来的着色会有非常大的噪声，说白了这个着色算出来是多少全靠运气，没关系，我们可以透过一个像素投射出多条视线，然后把所有视线计算出的 Radiance 平均起来作为这个像素的结果：

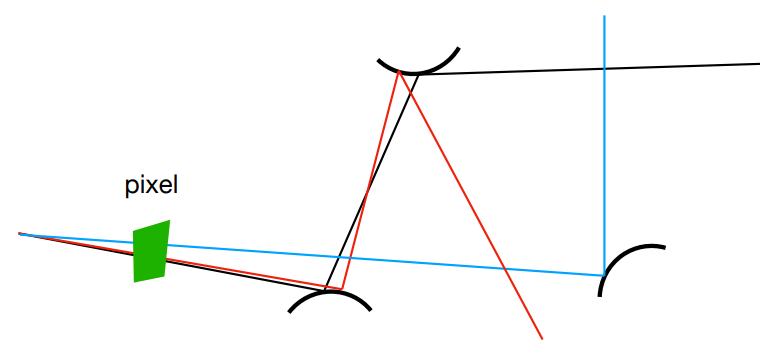
因此我们可以再写一个生成视线的函数：

ray_generation(camPos, pixel)
    Uniformly choose N sample positions within the pixel	//在每个像素内选择N个采样点
    pixel_radiance = 0.0
    For each sample in the pixel
        Shoot a ray r(camPos, cam_to_sample) 	//每个采样点投射出一根光线
        If ray r hit the scene at p		//如果光线打到了着色点就调用着色函数
            pixel_radiance += 1 / N * shade(p, sample_to_cam) 
    Return pixel_radiance

这样就OK了，如果这时候代码都写完了而且能正确运行了，我们会发现渲染一张图片还是迟迟渲染不出来，这回绝不是因为效率太低，而是因为我们的着色函数是递归调用的，但是没有递归结束的条件。因此我们需要设定一个结束条件，最简单的就是规定弹射多少次就不再计算了，毕竟之前我们也看过渲染效果，弹射 4 次和弹射 16 次渲染出来的效果不会差太多，但是给定弹射次数太少会直接切断能量的传播，如果给定次数太多又有很多计算没有意义，因此这里要用一种相对妥善的解决方案，叫做俄罗斯轮盘赌（Russian Roulette ），简称 RR，这类似于左轮手枪装弹后，再把弹匣一转，这时候打出子弹的概率如果是 P，那么打不出子弹的概率就是 1 - P，我们借鉴这样的方法，给定一个生存概率 P，每次还是按照正常流程计算 Lo，并且以 P 的概率返回 Lo / P，以 1 - P 的概率返回 0 ，这样当返回 0 的时候递归就终止了，也就是递归每次会有 1 - P 的概率中止。

可是为什么这样做呢？这是因为这样做可以保证我们最终计算出的 Lo 的期望是正确的。上面的方法相当于就是一个最简单的二值分布，那么它的期望就是：
$$
E = P * \frac{Lo}{P} + (1-P)*0 = Lo
$$
也就是说按照 RR 的方法我们既能保证中止递归，还能期望得到正确的 Lo ，非常巧妙！

体现在代码上：

shade(p, wo)
    Manually specify a probability P_RR		//给定一个生存概率
    Randomly select ksi in a uniform dist. in [0, 1] 	//随机生成一个[0,1]之间的数
    If (ksi > P_RR) return 0.0;		//如果这个数大于生存概率，直接返回0，对应1-P的情况
    //否则和之前一样，但是要记得除以生存概率
    Randomly choose 1 direction wi~pdf		//随机的选择1个方向	
    Trace a ray r(p, wi) 		//从这个方向打出一条光线
    If ray r hit the light		//如果这个光线能到达光源，就按照公式计算着色
        Lo += (1 / N) * L_i * f_r * cosine / pdf(wi) / P_RR
    Else If ray r hit an object at q	//如果达到了其他物体表面，就递归地计算
        Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR
    Return Lo

现在我们就基本得到了一个正确版本的路径追踪算法。当然这个算法还有问题，那就是我们对一个像素投射出多条光线，可又该投射多少呢？如下图：

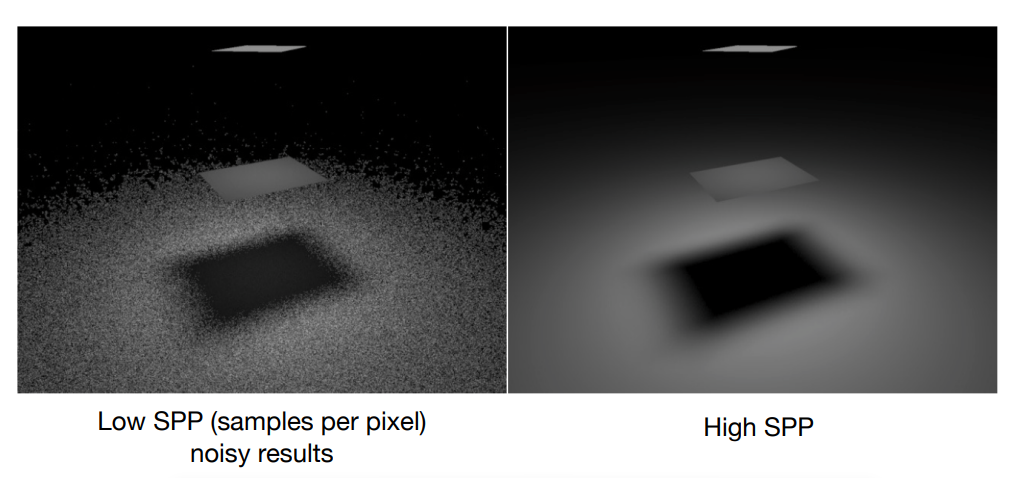
对每个像素的采样数量简称为 SPP，SPP 低的时候得到的结果噪声会很大，这很好理解；而 SPP 高的时候效果很好但是效率又非常低，前人大佬们自然是不能容忍这样的问题存在的，那能不能既快效果又好呢，一定是可以的。

考虑我们现在的方法，只跟踪一条光线，这条光线再朝哪个方向投射光线是完全随机的，对于下面几种情况：

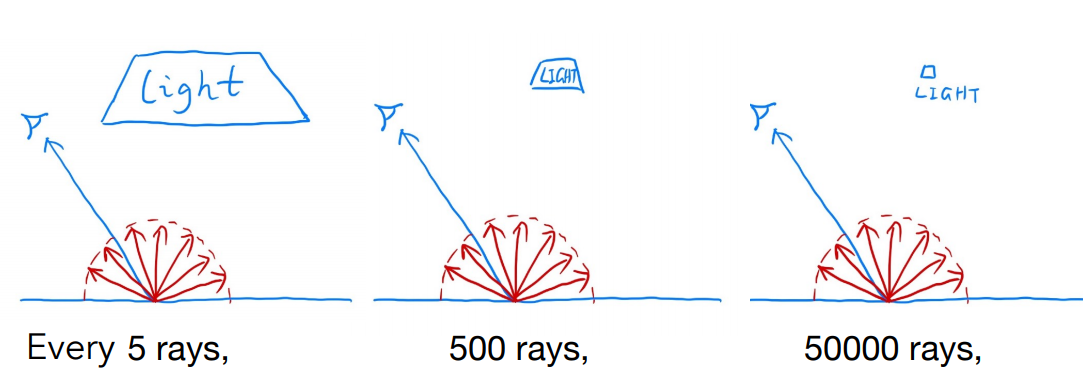
如果场景的光源面积很大，那投射出的光线到达光源的概率就高，可能每 5 条光线就有 1 条能打到光源上，就能计算出一个值；可如果光源面积很小，可能我们投射出了很多光线，但都没有打到光源上，那么这些光线就是没用的，对我们的计算结果没有任何影响，完全浪费掉了，可我们明明知道光源在哪，为什么还要随机选择投射方向呢？

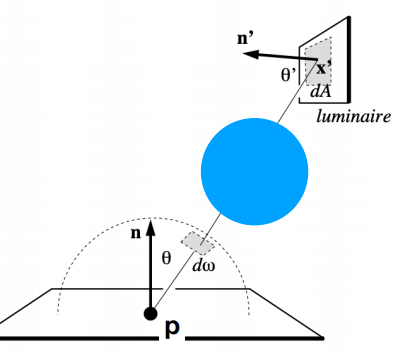
我们完全可以直接对面光源进行采样，直接在光源上进行采样，这样就能保证每一条光线都能打到光源上，一个都不浪费，但是蒙特卡洛积分要求，对谁积分就得对谁采样，因此我们要对光源平面 $dA$ 采样，就得把渲染方程对 $d\omega$ 的积分改写成对 $dA$ 的积分，实际上就是积分变量替换，只要找到 $dA$ 和 $d\omega$ 的关系就可以了。

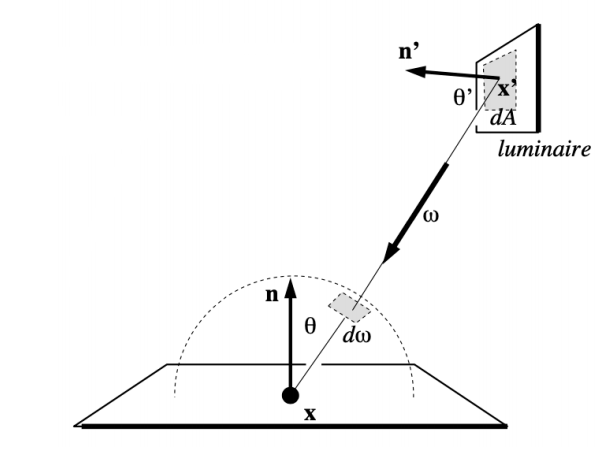
我们知道 $d\omega$ 是立体角，立体角的定义是从球心向球面上投射出的一块区域的面积和球半径平方的比值，那么 dA 的立体角就是 dA 在球心方向的投影的面积除以到球心的距离的平方，而立体角是指示方向的，所以 dA 的立体角和 $d\omega$ 表示的是一样的，因此二者相等，所以可以得到：
$$
d\omega = \frac{dA \ cos\theta’}{| x’ - x |^2}
$$
于是渲染方程就可以改写为：

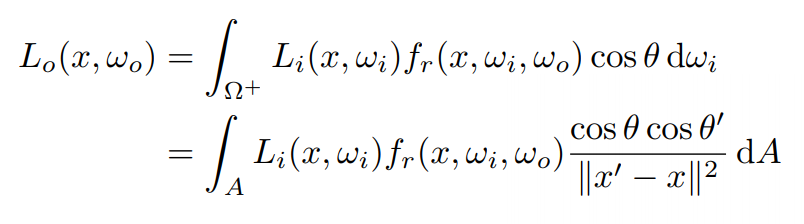
同时，对于一个面光源 A，均匀采样的概率密度函数就是：
$$
pdf = \frac{1}{A}
$$
这样也就可以用蒙特卡洛积分解方程了。

因此路径追踪的算法又要改一下，现在我们一个着色点从其他地方入射来的 Radiance 就分为两部分：

• 一部分来自光源，这部分直接对光源采样，按照上面的改写后的积分计算结果即可，并且不需要 RR 控制终止
• 另一部分来自其他物体表面反射，按照原来的积分计算结果，并需要 RR 控制终止

于是现在的路径追踪算法的伪代码就是：

shade(p, wo)
    //来自于光源的部分
    Uniformly sample the light at x’ (pdf_light = 1 / A)	//在光源平面采样
    L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light		//计算着色
	
    //来自其他的部分
    L_indir = 0.0
    Test Russian Roulette with probability P_RR
    Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi) 
    Trace a ray r(p, wi)
    If ray r hit a non-emitting object at q		//这里判断要改成光线打到非光源上才计算，不然就和上面重复了
        L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR 
    
    Return L_dir + L_indir

到此为止我们就得到了一个完全正确的路径追踪算法。

还有最后一个小问题，如何判断在光源平面采样的光线和着色点之间是否有阻挡？

只需要从着色点再打出一条光线看能不能达到光源就可以了，如果有阻挡，这条打出去的光线就会碰到其他物体。

现在可以说路径追踪的全部入门内容就彻底结束了！

最后来看看路径追踪的效果：

左边是一张真实的相机拍摄的图片，右边是路径追踪算法渲染出来的图片，可以看到渲染的非常真实，可以说是无限接近真实场景，这就是路径追踪的强大之处。

7 总结

以上就是路径追踪的全部基础内容，看似已经非常细节了，但实际上还有无数的细节问题没有讨论到，比如：

• 如何对一个球面均匀采样？
• 蒙特卡洛积分采样的概率分布是不是应该根据渲染的场景来选择合适的分布才能达到更好的效果，均匀采样只是最简单的一种；
• 随机数的质量直接影响渲染效果，如何生成分布均匀概率准确的高质量随机数？
• 是不是可以把着色点的方向采样和光源平面采样结合起来以达到更好的效果？
• 渲染方程计算出来的就是最终显示在像素上的颜色吗？当然不是的，还要经过伽马矫正等一系列操作才能转变为颜色，而颜色这部分还涉及到颜色空间，HDR之类的问题……

所以我们看似搞懂了路径追踪，其实最多也只能算是刚刚入门，还有太多的东西没有了解到。这一路过来可以说整个路径追踪的流程非常复杂，光是最基础的理论推导都如此困难，那想把代码写对就更是难上加难，并且永远不要忘了我们还只是在学习前人留下的经验。这节课最后闫令琪老师说的话对我的启发非常大：“我学了十年渲染，至今还觉得我什么都不会”。更何况你我呢？

敬畏科学，学无止境。