辐射度量学(Radiometry)
上一节我们学习了 Whitted 风格光线追踪的基本原理和优化结构,Whitted 风格光线追踪是基于布林冯光照模型的渲染方式,回顾布林冯光照模型,其中有一个概念我们一直不清楚,那就是所有光照公式中的光照强度 $I$ 是如何定义的,光照强度到底是什么,是从哪里来的,又要用什么去衡量?并且上一节中我们也看到了,其实利用 Whitted 风格光线追踪渲染出来的图片并没有想象中那么真实,这是因为我们从头到尾都没有准确的对光照进行度量和描述,所有公式中的光都是抽象的,简化的结果。因此也无法解释上面的一系列问题。
从这一节开始我们将学习更为先进的路径追踪技术,路径追踪技术是基于辐射度量学的光线追踪算法,而辐射度量学是可以准确描述光线的空间属性的体系,可以保证在物理上绝对正确的情况下进行各种光照的计算。
为了之后更好的学习,这一节首先介绍基础辐射度量学的各种概念和公式,由于许多概念没有太准确的中文翻译,所以这一节中的概念只能在保留英文原词的基础上尽可能的加以说明。
1 Radiant Energy 和 Flux(Power)
Radiant Energy 简单来说就是指光线的能量,物理上能量的单位是焦耳(J),所以 Radiant Energy 的单位自然也是焦耳。
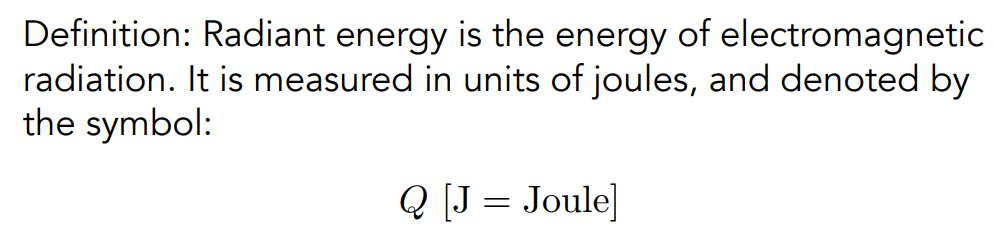
Radiant Flux 物理上叫做辐射通量,也称为功率(Power),是指单位时间内,放射、反射、折射或者接收到的光的能量,物理上功率的单位一般是瓦特(W),光学中有一个专门的单位流明(lm)。
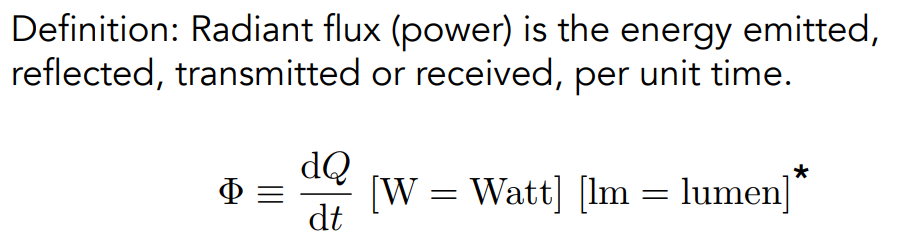
辐射通量还可以理解为一个光源放射出光线,在单位时间内通过一个平面的光线的数量,这样理解更符合”通量“这个概念,但辐射通量(功率)用我们生活上的经验来理解指的其实就是”亮度“,比如我们买灯泡,功率越大肯定就越亮,所以 Radiant Flux 描述的就是光的亮度,因此功率就代表光的强度。后文中提到的所有光的强度指的都是辐射通量,也就是功率。
2 Radiant Intensity
之前我们一直不知道如何描述一个点光源向四面八方辐射出的光线的强度,因为我们不知道如何定义空间中任意一个方向。回顾平面中我们是如何定义任意一个方向的:
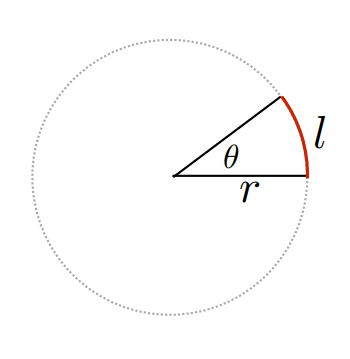
显然是用角度来定义的,一个单位圆就可以定义平面中任意一个方向,高中知识也告诉我们这个角度等于弧长除以半径,因为整个圆的周长是 $2\pi r$,所以角度最大就是 $2\pi$,单位是弧度(radians)。那这个概念能不能推广到空间中呢?当然可以。
空间中的一个单位球就可以定义任意一个方向,从圆心向球面投射出一块小的区域 A ,当这个区域足够小的时候这个锥体就指示了一个方向,我们用这个椎体的面积除以球的半径的平方就得到了类似于二维中的角度,我们把这个角度称为立体角(Solid Angle),因为球的表面积是 $4\pi r^2$,所以立体角最大是 $4\pi$,单位是 sr(steradians).

Radiant Intensity 就是用来描述一个点光源放射出的单位立体角上的光的强度的物理量。所谓单位立体角,我们永远可以理解为它就是一个方向。这句话非常关键,对于后面其他概念的理解很有帮助。
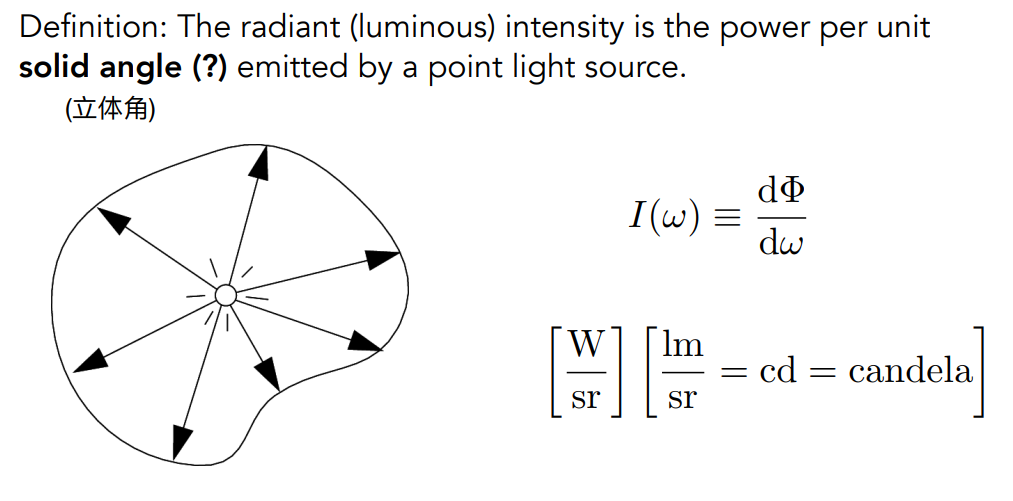
根据上面的公式,Radiant Intensity 的单位是(lm / sr),有一个专门的名字叫做 candela,candela 也是国际标准单位之一。
其中微分立体角 $d\omega$ 如何表述呢?可以利用微积分知识得到另一个表达式,考虑空间中的单位球体:
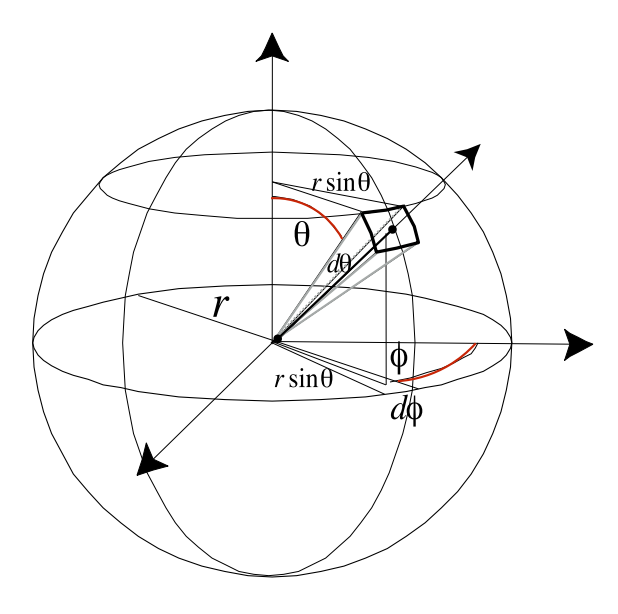
实际上之前定义空间中任意一个方向我们更为熟悉的方式是用角度 $\theta$ 和 $\phi$ 来唯一确定球上任意一个半径方向,也就指示了空间中任意一个方向,其中 $\theta$ 是半径与 Z 轴的夹角, $\phi$ 是半径绕 Z 轴旋转的角度。那么考虑一个单位立体角,假设这个立体角是半径分别在 $\theta$ 和 $\phi$ 方向上移动 $d\theta$ 和 $d\phi$ 角度形成的,于是它对应球面上一个非常小的矩形 $dA$,我们要计算这个矩形的面积就要求出它的两个边长,矩形垂直的边长对应的就是以 $r$ 为半径的圆上的一段圆弧,圆弧对应的角度是 $d\theta$ ,所以矩形的垂直边长就是 $r·d\theta$,同理矩形水平的边长对应的是以 $r·sin\theta$ 为半径的圆上的一段圆弧,圆弧对应的角度是 $d\phi$ ,所以矩形的水平边长就是 $r·sin\theta ·d\phi$,因此可以得到微分矩形的面积:
$$
\begin{split}
dA &= (r·d\theta)(r·sin\theta ·d\phi) \\
&= r^2 sin\theta \ d\theta \ d\phi
\end{split}
$$
于是微分立体角就是:
$$
d\omega = \frac{dA}{r^2} = sin\theta \ d\theta \ d\phi
$$
之前说过,因为立体角表示的是整个球面上某一块的面积与半径平方的比值,所以立体角最大就是 $4\pi$,因此在球面上对所有立体角 $\omega$ 积分一定得到的是 $4\pi$,整个球面对 $\omega$ 积分实际上就是对 $\theta$ 在 $[0,\pi]$, $\phi$ 在 $[0,2\pi]$ 上积分,就是一个简单的二重积分:
$$
\begin{split}
\Omega &= \int_{S^2} d \omega \\
&=\int_{0}^{2\pi} \int_{0}^{\pi} sin\theta \ d\theta \ d\phi \\
&= 4\pi
\end{split}
$$
现在再回顾 Radiant Intensity 的定义,Radiant Intensity 描述的就是一个点光源朝四面八方辐射出去的光的通量(功率)。如果我们假设一个点光源向各个方向辐射出的强度是相同的,那么每个单位立体角上的强度就是一样的,假设为 $I$,则光源本身的强度 $\Phi$ 相当于每个单位立体角上的强度 $I$ 的积分:
$$
\begin{split}
\Phi &= \int_{S^2} I \ d\omega \
&= 4\pi I
\end{split}
$$
因此每个单位立体角上的强度 $I$ 就是:
$$
I = \frac{\Phi}{4\pi} \ (candelas)
$$
比如一个 LED 灯泡的功率是 815 流明,那么它的 Radiant Intensity 就是:
$$
Intensity = \frac{815 \ lm}{4\pi \ sr} = 65 \ candelas
$$
3 Irradiance
Intensity 是用来描述一个光源发出的光的强度的物理量,那自然要有一个物理量用来描述一个点接收的光有多少,Irradiance 表示单位面积入射的光的强度,单位是 $lm / m^2$,也有一个专门的名字叫做 lux。
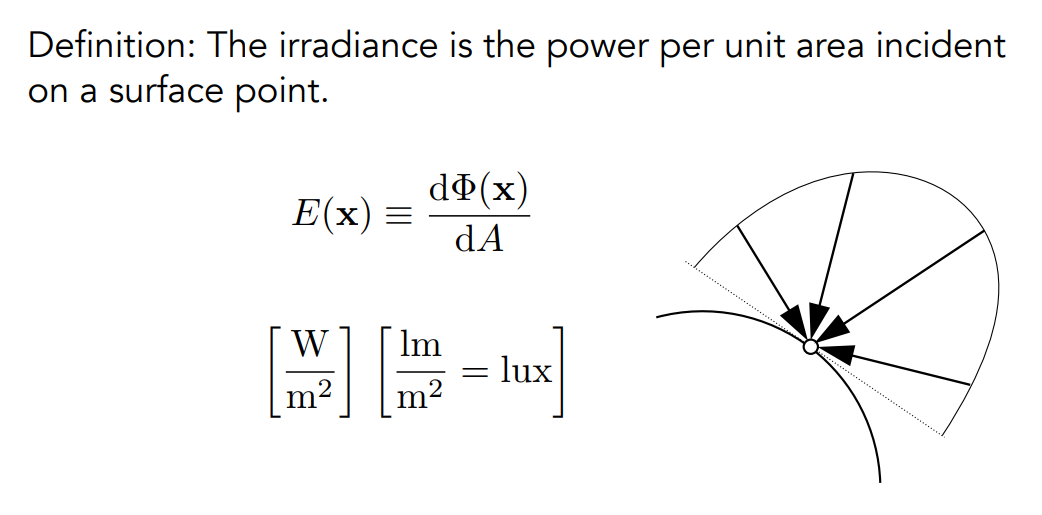
这里的单位面积指的是投影单位面积,我们规定只有光线和这个面垂直,才去计算 Irradiance,因此如果这个面和光线入射方向不垂直,那就把这个面投影到垂直的方向上再计算,实际上这也是之前布林冯光照模型中用到的 Lambert’s 余弦定理的原理。
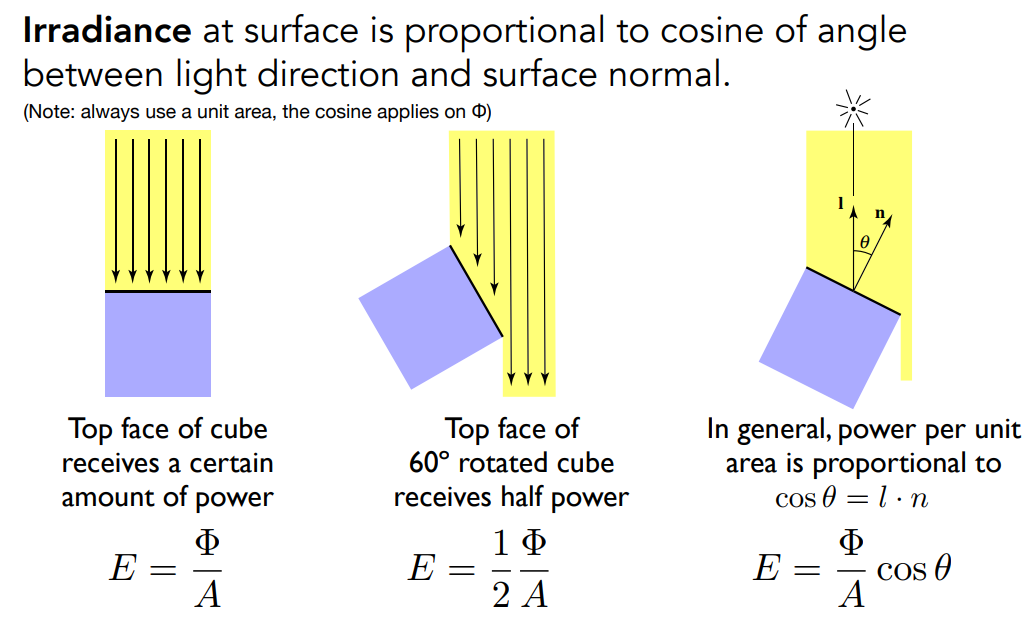
因此一个表面和入射光的夹角越接近直角,它单位面积接收到的光的能量就越大。
利用 Irradiance 还可以解释布林冯光照模型中光的强度随距离衰减为什么是 $I/r^2$。回顾当时的一张图:
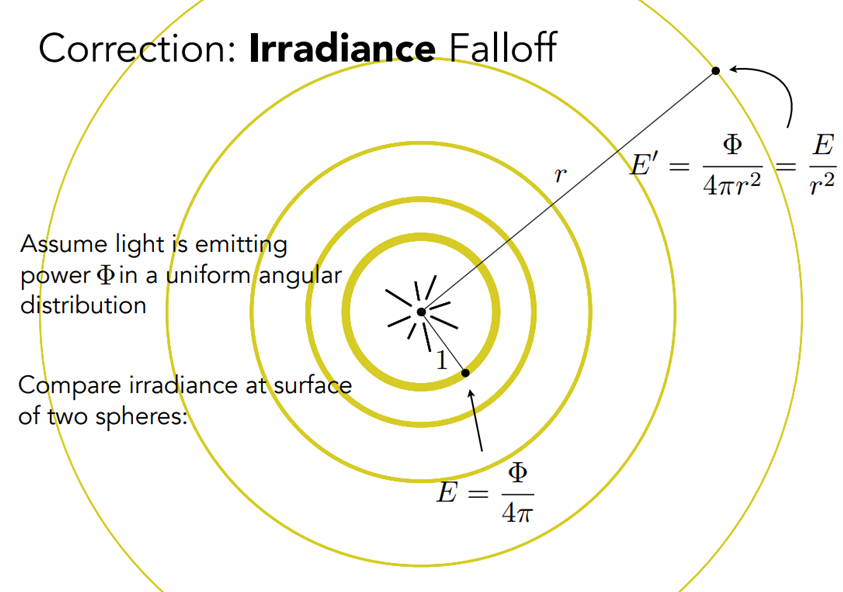
现在我们用辐射度量学的角度来理解这张图,如果光源的强度是 $\Phi$,假设光源向四面八方都是均匀辐射的,在光源处有一个单位球面把光源包起来,那么这个球面上每一处的 Irradiance 就是光源的强度除以球的表面积,单位球半径为1,因此:
$$
E = \frac{\Phi}{4\pi}
$$
而距离光源半径为 $r$ 的球面上每一处的 Irradiance 就是:
$$
E’ = \frac{\Phi}{4\pi r^2} = \frac{E}{r^2}
$$
所以之前说的光的强度随距离衰减实际上是 Irradiance 在随着距离衰减。
4 Radiance
到目前为止,我们已经有了描述光源发出的光的强度的物理量 Intensity 和描述单位面积接收到的光的强度的物理量 Irradiance,接下来就是最重要的一个概念——Radiance,Radiance 是用来描述光线的物理量,而我们后续渲染时的所有计算都是基于光线的计算,所以说 Radiance 是最重要的一个概念。
Radiance 定义为单位立体角、单位投影面积上发射、反射、折射或入射的光的强度。单位是 $lm/(sr·m^2)$,也有一个专门的名字叫做尼特(nit)。
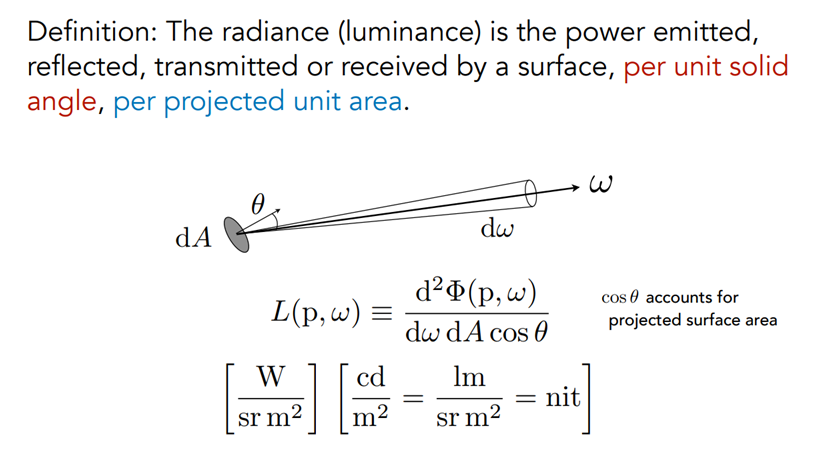
虽然已经有了心理准备,但这个概念还是太过抽象了。不过我们可以一点一点拆开来看。从上面的公式可以看到,实际上 Radiance 就是单位立体角、单位面积的光的强度。
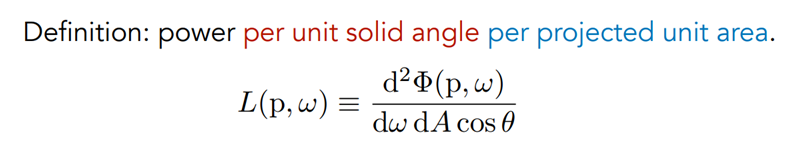
回顾 Radiant Intensity 的定义,Radiant Intensity 是单位立体角上的光的强度,那么 Radiance 不就是单位面积上的 Radiant Intensity 吗;同理,Irradiance 是单位面积上的光的强度,那么 Radiance 不也可以是单位立体角上的 Irradiance 吗。
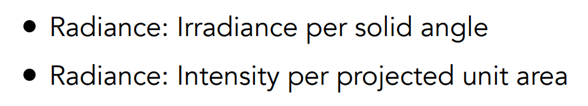
现在我们在抽象上好像明白 Radiance 是什么了,接下来分别分析一下这两种说法对应的都是什么物理意义。
- Radiance 相当于单位面积上的 Radiant Intensity,Radiant Intensity 是指一个点光源放射出的单位立体角上的强度,所以Radiance就是一个光源单位面积上放射出的单位立体角的上的光的强度。之前说过,单位立体角我们永远可以理解为它就是一个方向,因此上面这句话就可以理解成一个光源单位面积上放射出的某个方向上的光的强度。这相当于我们不考虑整个光源向某个方向放射出的能量有多少,而是只考虑光源上的某一个单位平面向某个方向放射出的能量有多少,同样这里的单位面积一定是投影单位面积。因此从这个角度来说,Radiance 表示的是沿着某个立体角表示的方向 $\omega$ 离开单位平面 dA 的光的强度。这里的”离开“自然可以代表发射、反射、折射等等。

- Radiance 相当于单位立体角上的 Irradiance,Irradiance 表示单位面积入射的光的强度,单位立体角又表示方向,所以Radiance 就是单位面积在某个方向上入射的光的强度。也就是一个单位平面从四面八方都会接收到光,但 Radiance 只表示这个单位平面接收到的从某个方向 $\omega$ 入射来的光的强度。

下面的图有助于更进一步理解 Radiance 和 Irradiance 的关系:
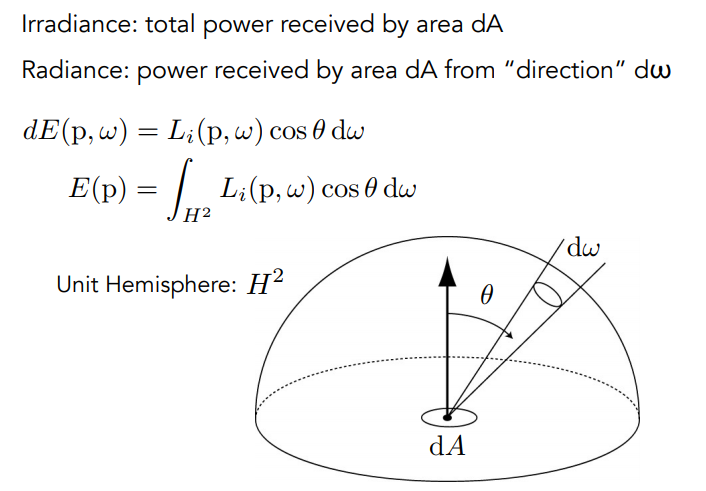
Irradiance 是单位平面 $dA$ 从各个方向接收到的全部的光的强度,Radiance 是单位平面 $dA$ 从单位立体角 $d\omega$ 方向接收到的光的强度,因此对 Radiance 在半球面的各个方向 $d\omega$ 上积分,得到的就是各个方向接收到的光的强度的总和,也就是 Irradiance 。
这样一来我们就可以理解 Radiance 的物理含义了,同时也就明白为什么开头说 Radiance 是表示光线的物理量,因为它既有方向,又有大小。