从这一节开始我们将了解图形学中的光线追踪(Ray Tracing)技术,包括经典的 Whitted 风格光线追踪技术和效果更好的路径追踪技术。并且在之后的高质量实时渲染专题中还会进一步学习最新的工业界实时光线追踪技术。
Whitted 风格光线追踪(Whitted-Style Ray Tracing)
1 为什么需要光线追踪?
之前我们学习了光栅化渲染的基本原理,光栅化中,一开始就假设了光源是点光源且光线只弹射一次,但在大多数实际场景中并不是这样的,比如:

Glossy 反射是指这种半磨砂材质的反射,这种材质用光栅化技术无法渲染的非常逼真,另外就是一些间接光照的场景,比如右边的图没有直接光源,但是因为光线在场景中弹射了许多次,所以我们可以看到整个场景中的各个物体。另外,上一节中我们学习了阴影映射,阴影映射生成的只能是边界清晰的硬阴影,无法生成更为逼真地软阴影。而光线追踪就可以解决以上这些问题,光线追踪尽可能地模拟光线的传播过程,对整个场景进行光照计算。
但并不是说光线追踪就比光栅化好,现在的大多数游戏中还是使用实时光栅渲染,因为光栅渲染的快速高效是光线追踪无法比拟的,比如 PUBG超大的地图,为了保证游戏正常运行只能使用光栅渲染,并且牺牲一些图像细节:

光线追踪能带来更好的画面细节,但速度慢,开销大,对硬件要求高,所以大多数情况下用来离线渲染一些动画、视频等,近些年游戏中的实时光线追踪技术我们将在另外一个专题更进一步讨论。

2 基础光线追踪算法
为了之后讨论光线追踪算法更方便,我们要先对光线做一个图形学上的定义,注意这里的图形学定义大多数都不符合物理学和光学规律,但一定是符合我们人类的直觉的。我们规定:
- 光是沿直线传播的
- 光线在发生交叉的时候不会产生碰撞,也就是光线传播互相不会产生影响
- 我们能看到物体是因为光线从光源经过一系列反射、折射达到了人的眼睛
虽然上面这些定义都不一定符合物理事实,但却为我们的光线追踪算法提供了很重要的思路,尤其是最后一条,也就是我们能看到的光线一定是达到了我们眼睛的光线。
2.1 光线投射
根据上面的核心思想,我们能看到的光线一定是达到了我们眼睛的光线,那么我们可以从眼睛投射出一条“光线”到物体上,把这条“光线”称为视线(Eye Ray),视线将会和场景中的物体相交,把交点和光源相连就构成了一条光路,于是就说明存在一条光路使光线从光源经过物体上的这个点射进我们的眼睛。这就是光线投射的思想。
我们把这个思想应用到渲染过程中,我们要把场景渲染到屏幕上才能被眼睛看到,因此我们就从眼睛透过屏幕上的每一个像素向场景中投射一条视线,这条视线会与场景中的物体存在很多交点,如下图,那么肯定离屏幕最近的交点才是我们能看到的点,也就是能显示在屏幕上的点,这一步相当于把屏幕上的像素所显示的场景中的点找到,并且顺便完成了深度测试。(注意体会和光栅化的区别)
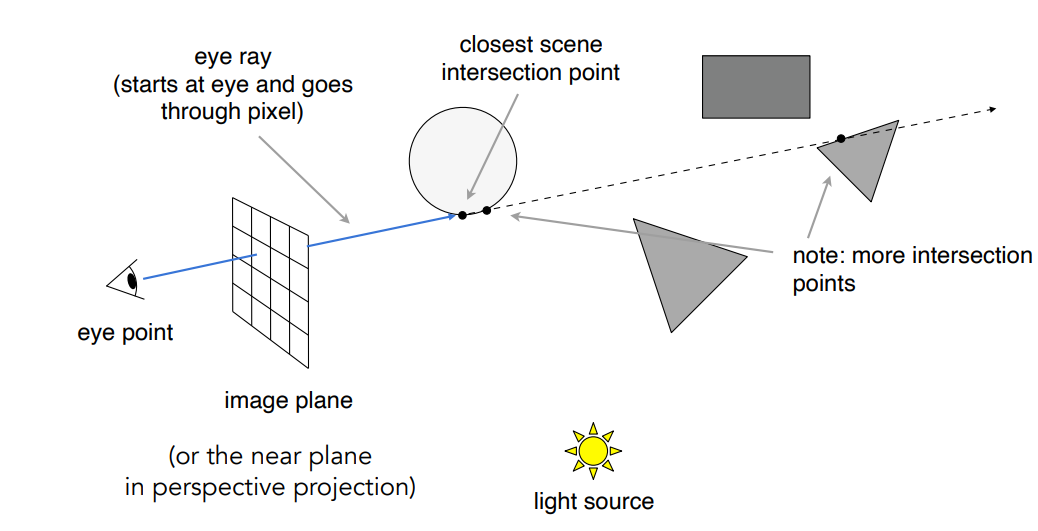
然后连接交点和光源,这样一来,我们相当于拥有了光线入射方向,平面法线方向和观察方向三个方向向量,那就可以计算这一点的着色了,计算完成后把这个着色显示在像素上,之后对每个像素都这么做就完成了整个渲染过程。
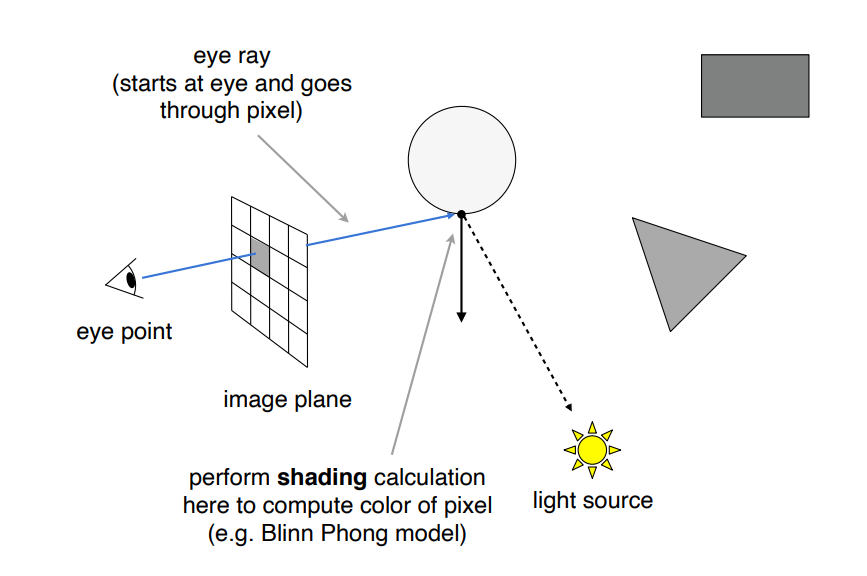
这只是光线投射的基本思想,到现在为止光线还是只弹射了一次,还谈不上“追踪”,要更真实的模拟光的传播就需要考虑光线的多次反射和折射,这就是 Whitted 风格光线追踪算法。
2.2 Whitted风格光线追踪
Whitted 风格光追是按照光线投射的思路递归地进行计算,具体过程如下:
还是从眼睛透过屏幕上的每一个像素向场景中投射一条视线,找到与场景中的物体最近的一个交点:
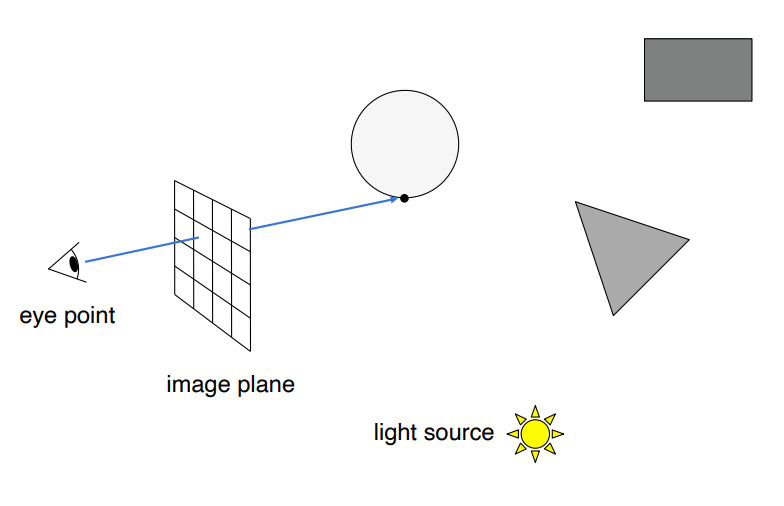
然后我们假设光线的反射是完美反射,也就是朝镜面反射方向传播,因此我们可以计算出反射后光线的方向,继续计算反射光线和其他物体的交点:
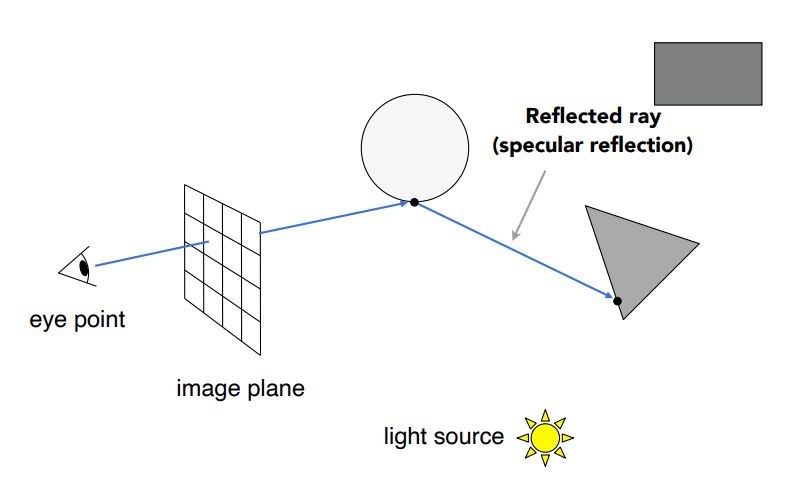
当然如果物体是透明的,那光线不止发生反射,还会发生折射,我们还可以计算折射光线:
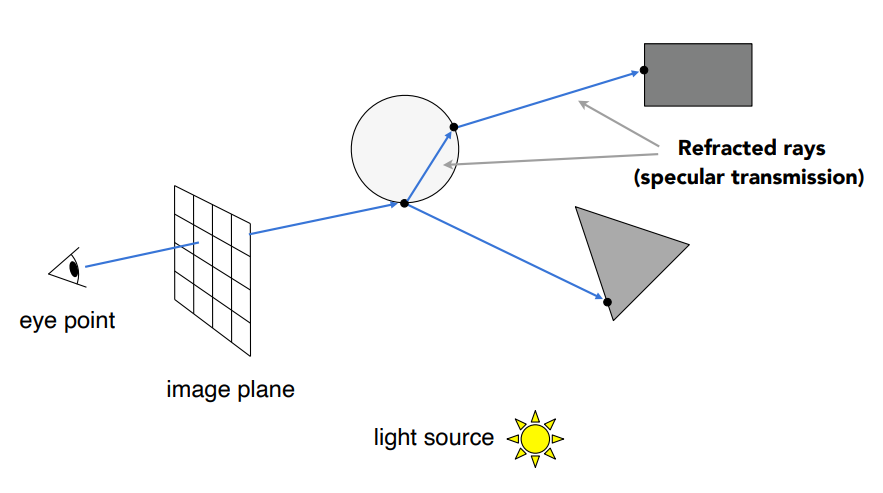
算出这些光线的交点之后,把这些交点全部和光源连接起来,那么这个示例场景中就形成了四条光路:
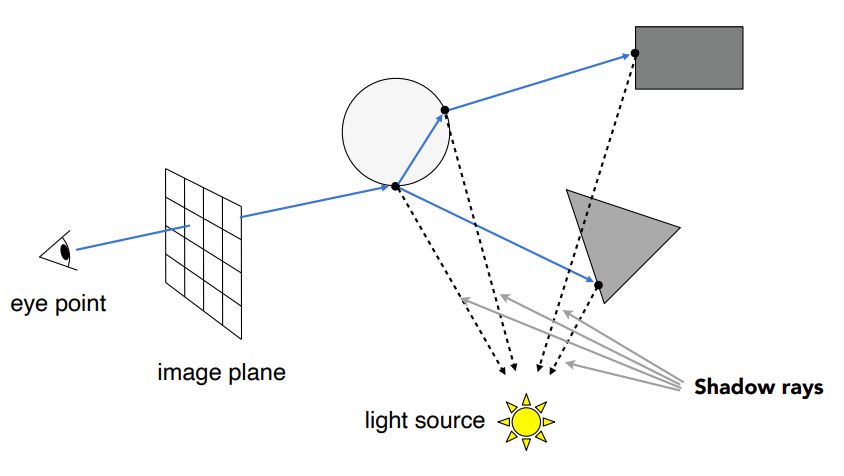
这些光路都是可以到达我们的眼睛的,因此我们计算每个点的着色,然后全部加起来给到这个像素上作为它显示的像素值。当然这里一定不是简单的累加,光线在传播过程中会有能量损失,具体到一个物体表面会有多少能量被反射,多少能量被折射是与材质有关的,我们只要知道把这些着色值全部作为像素显示的一部分就可以了,因为这些都是可以被看到的部分。下面是光线追踪渲染的一个效果图,可以看到透明球体的折射也显示出来了,并且透明球体的阴影也要比实心球体暗一些。

那么了解了基本原理接下来就是解决具体的实现问题了,上面的流程中第一个要解决的问题就是如何计算视线和场景中物体的交点。
3 光线和平面的交点
3.1 光线的数学定义
这里的光线是广义的,就是指空间中一条射线,自然也可以是视线,定义很简单,空间中只要给定一个出发点和一个发射方向(单位向量)就可以唯一确定一条射线,如下图:
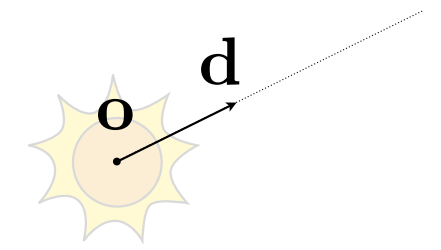
那么光线在时刻 t 所在的位置就可以表示为:
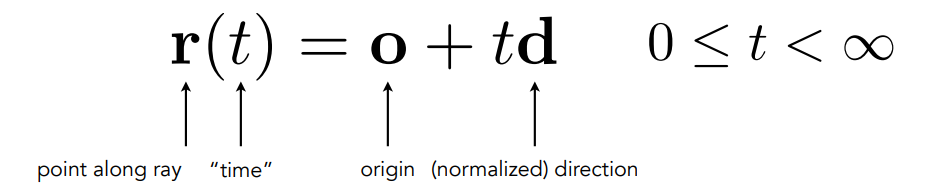
3.2 隐式表示求交点
有了光线的数学定义,如果我们有物体的隐式表示,比如代数方程,那么很容易可以求出光线和物体表面的交点。以球面为例,对于空间中以 $c$ 为球心,$R$ 为半径的球面上的任意一点 $p$,代数形式可以表示为:
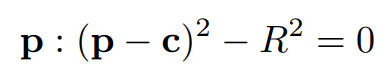
我们要求光线和球面的交点,也就是联立两个方程求光线传播时间 t :
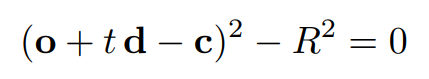
整理一下可以得到一个关于 t 的一元二次方程,剩下的就是高中数学知识:
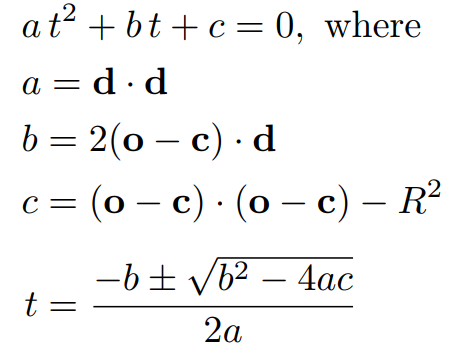
这里要特别强调的是 t 的物理意义,t 表示光线传播的时间,因此 t 需要大于0,并且必须是实数,所以要得到光线和物体表面离屏幕最近的一个交点就相当于解方程求一个最小的正实根。这个方法自然也可以推广到任意用隐式方程表示的物体:

至于有些方程非常难解这个不需要我们担心,计算机本身也是用数值方法求解方程,所以无论多复杂都一定可以求出满足条件的解,关于复杂方程的数值求解方法这不是我们讨论的重点。
3.3 显示表示求交点
上面说的隐式方程求交点是我们早就了解的数学知识,只是应用到了这里,但通过之前的学习我们知道,图形学中更常用的表示方法是显式表示,并且计算光照、阴影等都要用显式表示去计算,因此计算光线和显式表示的交点是必须要解决的问题,并且解决了这个问题还可以顺便解决之前我们提到的,显式表示不好判断一个点是否在物体内部的问题。
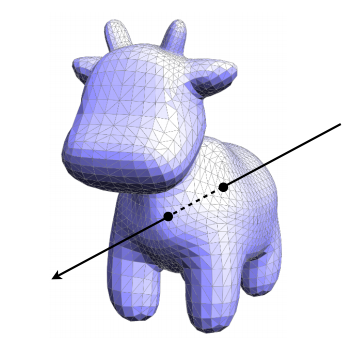
先说明如何通过光线和物体的交点判断一个点是否在物体内部。我们可以从空间中任意一点向任意方向发出一条射线,如果这条射线和物体表面有奇数个交点,那么它就在物体内部,如果有偶数个交点就一定在物体外部。可以在二维中验证这一理论。
接下来具体讨论如何计算光线和显式表示的物体表面的交点。最简单的方法就是和每一个三角形计算交点,全算完之后就可以得到和物体的交点,但这显然太慢了,屏幕上每个像素投射一条视线,然后每条视线和场景中每个三角形计算一次交点,并且还要计算光线反射和折射之后的其他交点,对于下图这样的复杂场景,有两千万个三角形,如果是一张 4K 的图,那这个计算量无法被接受的,因此一定需要做加速,具体如何加速我们之后再看,在这之前要先了解怎么计算光线和一个三角形的交点。

直接求光线和三角形的交点是不容易想到的,那我们可以分两步进行,先求光线和三角形所在平面的交点,再判断交点是否在三角形内部即可,而这两步计算都是很简单的。
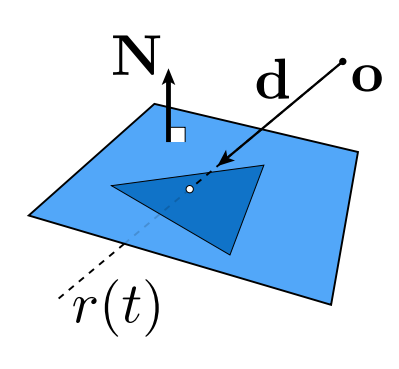
先考虑空间中对一个平面的定义,只要给定空间中一个点和一个法向量就可以唯一确定一个平面:
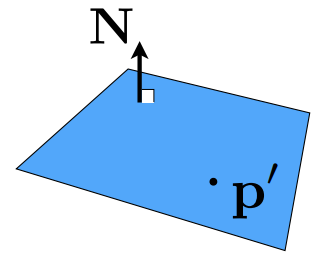
于是平面上任意一点就可以表示为:
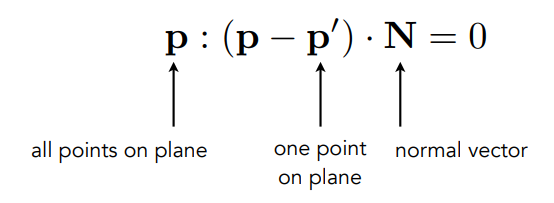
那么求光线和平面的交点同样联立解方程即可,这次的方程还更加简单:
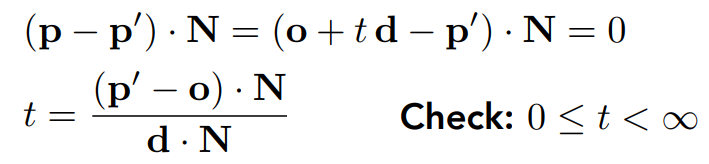
至于算出交点后如何判断在否三角形内部就不多说了。
上面是分了两步计算光线和三角形交点,那能不能直接计算呢?当然是可以的,这个计算的方法叫做 MT 算法(Möller Trumbore Algorithm),实际上也很简单。
回顾之前学过的三角形重心坐标,利用三角形的重心坐标可以表示三角形所在平面上的任意一点,因此光线和平面的交点一定满足:
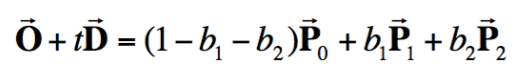
还是解方程,这里有三个未知数 $t、b_1、b_2$,而所有的坐标也都是三维坐标,所以这个关系式实际上表示的是一个三元一次方程组,利用克莱默法则可以快速求出解向量:
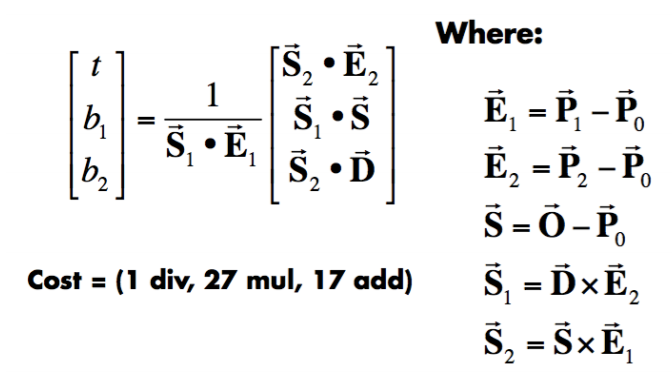
当然还是要保证解出来的 t 为正才有意义,同时也可以直接判断交点是否在三角形内部,因为三角形内部的点重心坐标非负。
知道了如何计算光线和三角形的交点,接下来就是一个更麻烦的问题,既然不可能每个三角形都算一次交点,那么如何加速?
4 交点计算加速
加速实际上就是减少计算交点的三角形个数,那么首先想到的就是把一个物体看作整体,先判断和物体有交点再去一个一个三角形具体计算交点在哪。
4.1 包围体(Bounding Volumes)
类似于Bounding Box ,我们用简单的几何体把物体包围起来,然后计算光线和这个几何体是否存在交点。

最常用的包围体自然是长方体,并且为了方便计算我们用的一般是轴对齐包围体(Axis-Aligned
Bounding Box),简称为 AABB ,所谓轴对齐包围体就是指包围体每个平面的法向量都和坐标系三个坐标轴对其,通俗的说就是一个“横平竖直”的长方体。然后为了便于理解,我们把空间中的长方体理解为是由三对平面的交集形成的几何体。也就是把六个平面想成无限大,这个立方体就是这六个平面相交的部分形成的。
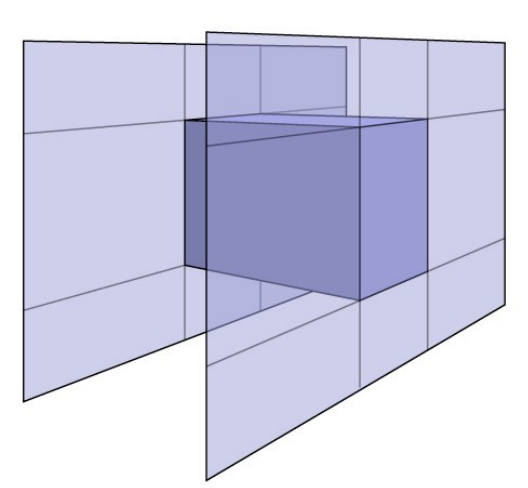
那么计算光线和立方体的交点就是计算光线和六个平面的交点,再加以判断即可。首先我们从简单的二维情况开始,先计算一条光线和一个长方形的交点:
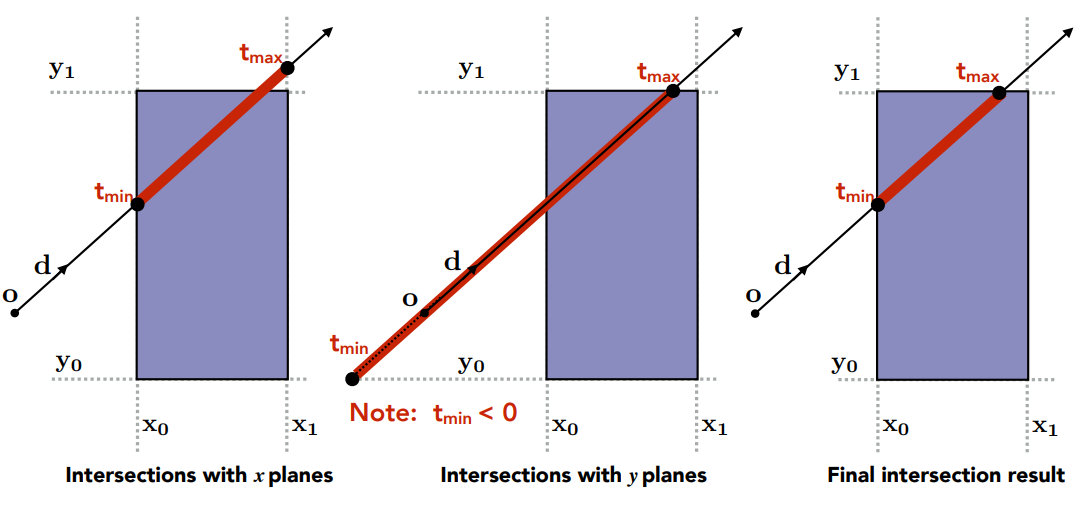
首先计算光线和长方形两条垂直边的交点,两条垂直边可以理解为一对平面 $x_0$ 和 $x_1$,可以得到一条线段,如上图左;
同理计算光线和长方形两条水平边的交点,两条水平边可以理解为一对平面 $y_0$ 和 $y_1$,可以得到另一条线段,如上图中,这里我们先假设光线是直线而不是射线,可以向两边延长,因此得到的 $t_{min}$ 可以为负数;
然后将得到的两条线段取交集就是光线在长方形内部的部分。
接下来推广到三维的情况,首先根据二维情况可以整理出两个关键的信息:
- 光线必须进入所有三对平面才代表光线进入了整个立方体
- 光线只需要离开任意一对平面就代表光线离开了整个立方体
基于上面关键信息,我们分别计算光线和立方体三对平面交点,得到三个 $t_{min}$ 和 $t_{max}$,那么光线在立方体中的部分就是:
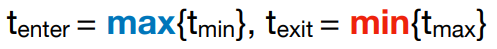
如果 $t_{enter} < t_{exit}$,那么就说明光线在这段时间是在立方体中的。接下来考虑几个特殊情况,刚才我们把光线当成了直线去计算交点,因此计算出来的 $t_{min}$ 和 $t_{max}$ 有正有负,所以最终得到的 $t_{enter}$ 和 $t_{exit}$ 也会有正有负:
- 如果 $t_{exit} < 0$,代表光线离开立方体的时间是负的,说明立方体在光线后面,因此光线不会和立方体有交点
- 如果 $t_{enter} < 0$ 且 $t_{exit} \geq 0$,代表光线起点就在立方体内,因此光线和立方体有交点
综上,光线和立方体有交点,当且仅当 $t_{enter} < t_{exit}$ && $t_{exit} \geq 0$.
回顾计算直线和平面的交点:
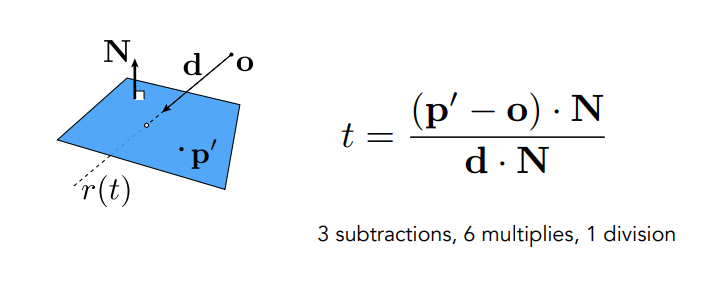
正常情况下我们要带入三维向量去计算,但是因为这里使用的是 AABB ,每个平面都和坐标平面平行,因此我们计算每对平面的交点时,只要用一个维度的坐标代入计算即可:
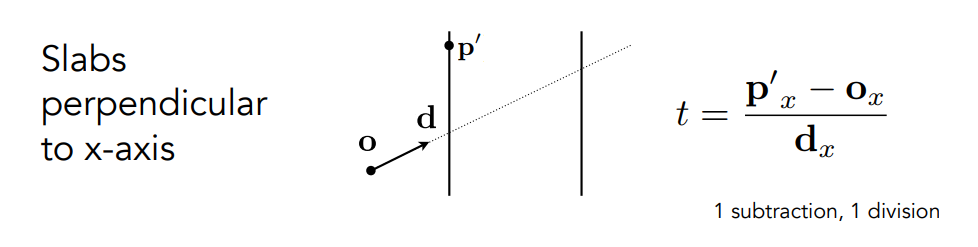
这也是使用轴对齐包围盒的原因之一,可以大幅减低计算量,使得计算光线和立方体的交点成为一个时间复杂度非常低的过程,为后续的优化奠定基础。
4.2 均匀空间划分(Uniform Spatial Partitions)
上面说了计算光线和三角形的交点不容易,但计算光线和立方体的交点非常方便,因此我们加速要尽量多做立方体判断以减少三角形计算。一种方法是对场景进行均匀空间划分,把给定的场景均匀的分成许多个小立方体,具体过程如下:
- 首先找到整个场景中所有物体的 bounding box;
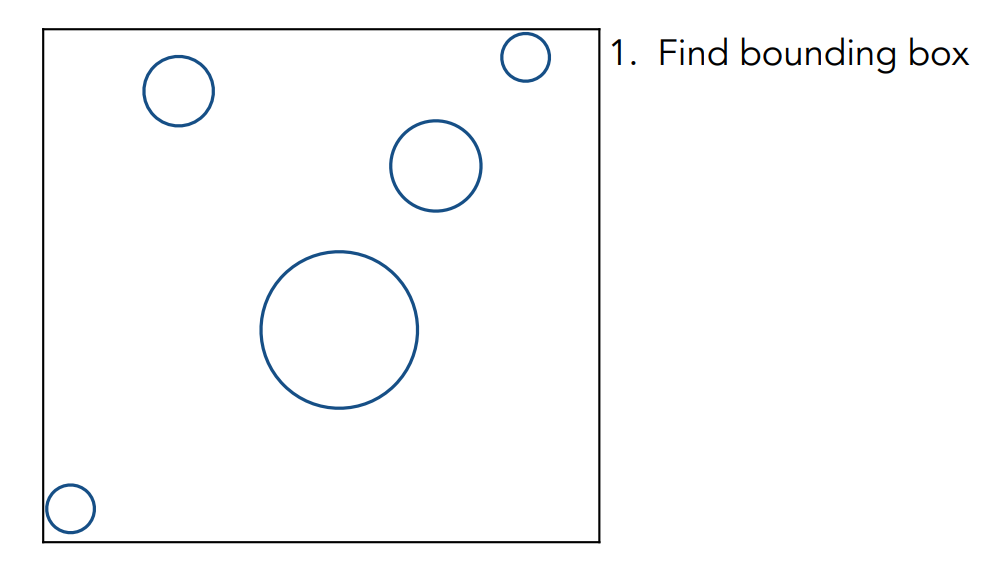
- 然后把把场景划分成均匀的网格:
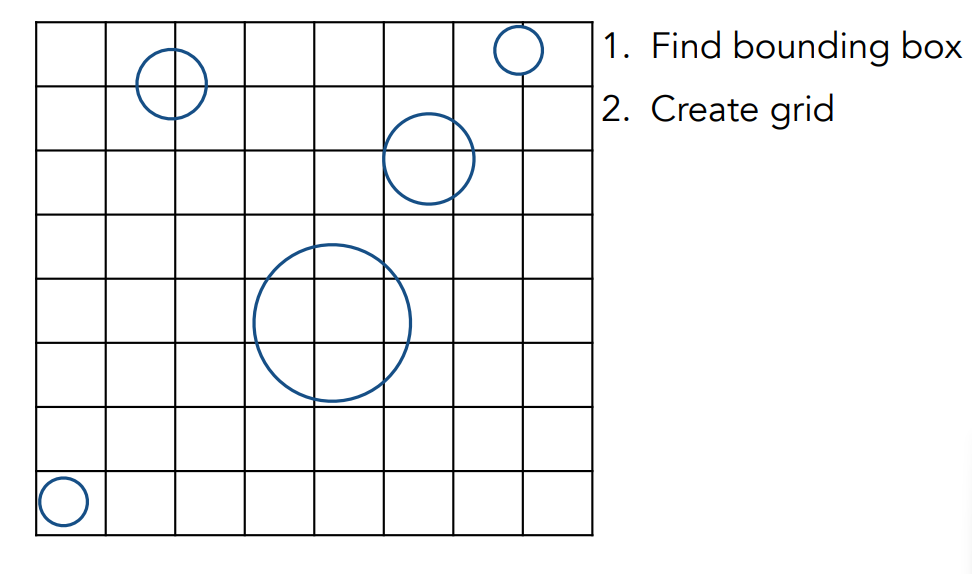
- 然后看哪些网格中包含了物体的表面,在这个网格中把这个物体存下来:
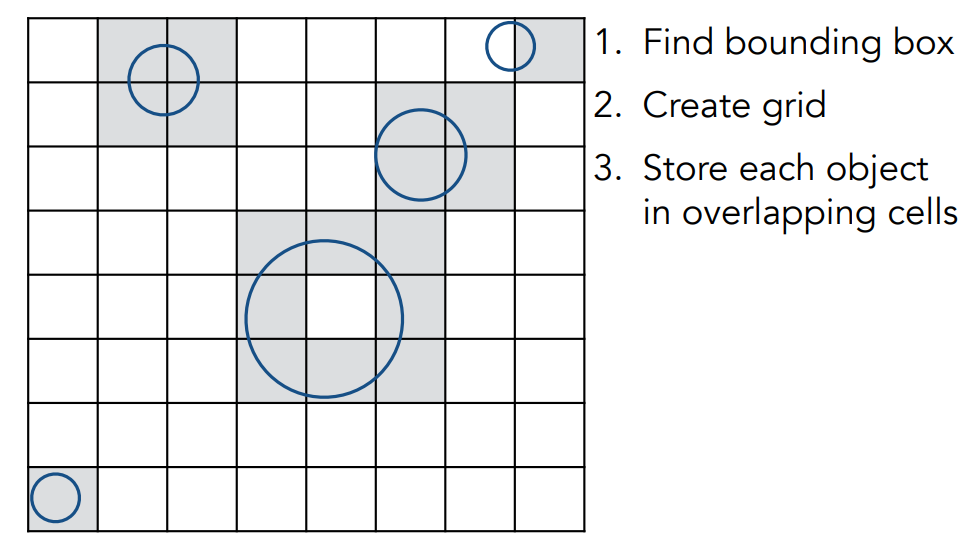
- 光线射入的时候计算光线经过的每个立方体,如果这个立方体内有物体,就计算光线和这个立方体内存储的所有物体的交点,至于光线经过了哪些立方体,可以用类似于光栅化中画直线的方法,就不多说了:
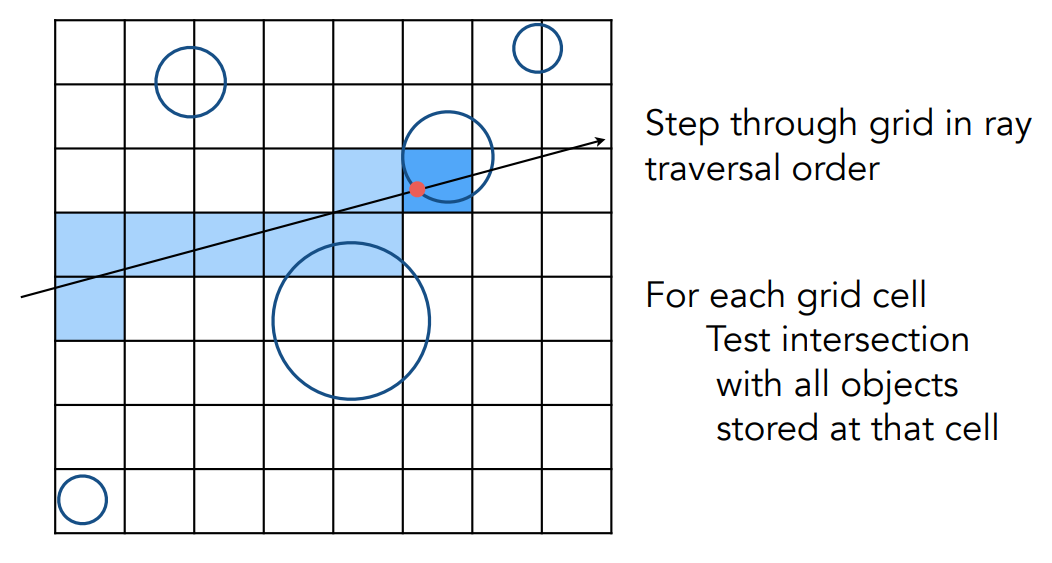
均匀空间划分的方法对于网格划分的密度很敏感,网格太小会导致效率很低:
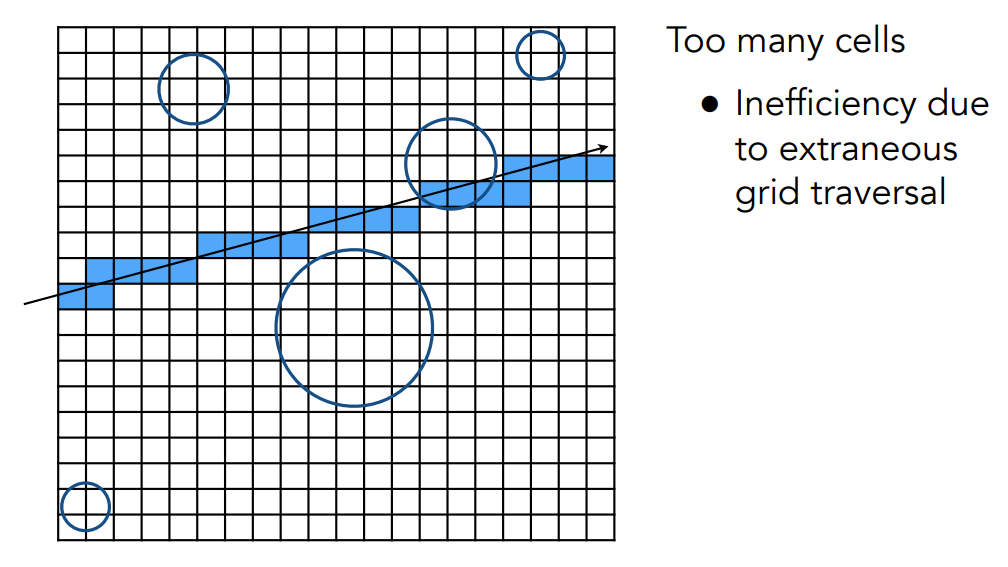
因此需要一个好的划分细度,人们根据经验得出一般把场景划分为 27 倍的物体数量个网格:
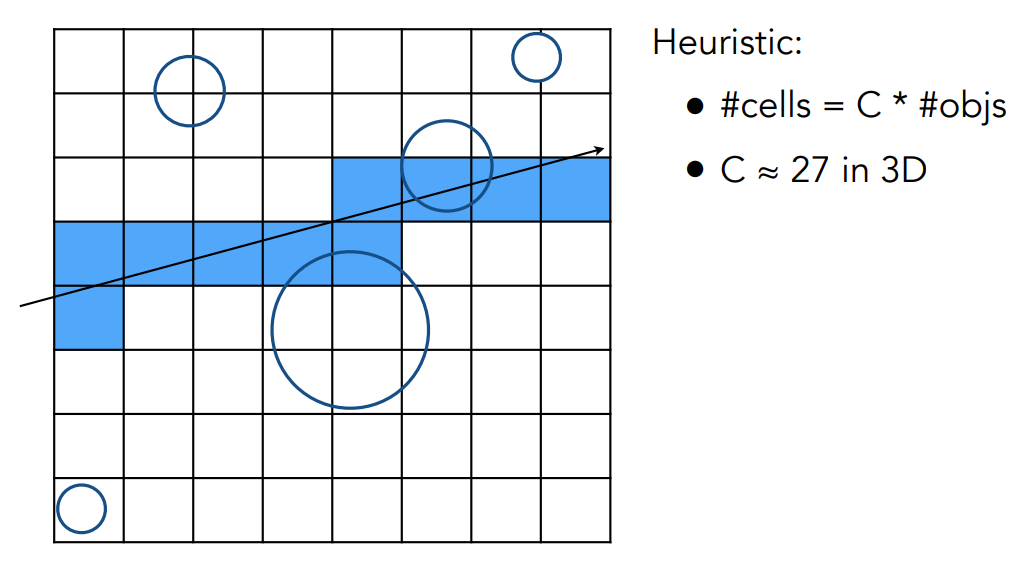
回顾均匀空间划分的方法我们发现对于物体很密集的场景,比如之前的草地,可以得到很好的效果,但是如果场景非常空旷,比如一个体育场中间有一个茶壶,那光线还是要经过许多次立方体的判断才能到达茶壶所在的立方体再去计算交点,因此我们希望空间划分不要非常均匀,很大一片没有物体的地方就可以划分成一个立方体,这样只要一次判断就能到达茶壶所在的立方体。
4.3 非均匀空间划分
非均匀空间划分是一个经典的问题,有许多非常成熟的方法,图形学中只是拿来应用,常见的有以下几种方法:
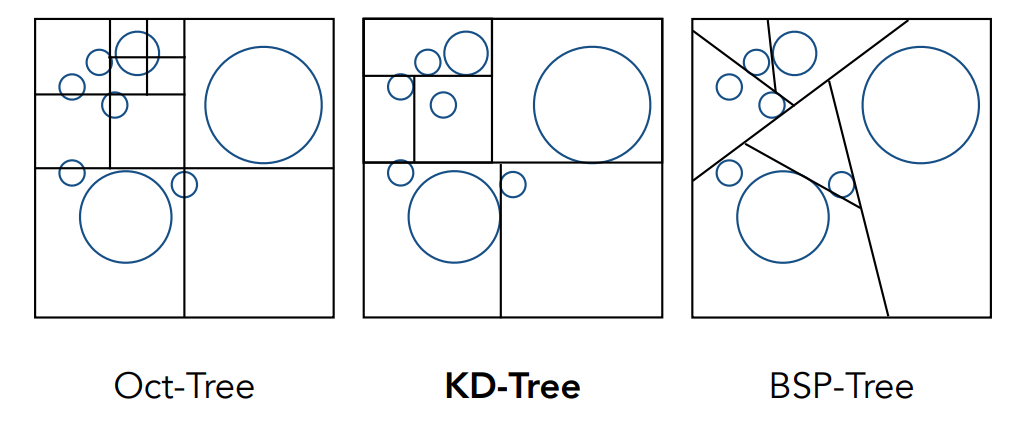
- Oct树也叫八叉树,每次把立方体均匀的分成八块,上图是一个立方体的侧视图,然后看分开的每个空间内物体的密度,如果没有物体或者只有很少个就不用继续分了,否则按照这种方法继续划分,这样划分出来的区域就有大有小
- KD树是八叉树的改良,八叉树在四维的时候就会变成十六叉树,更高维会呈指数增长,并且每次都是平均分,并不灵活。KD树每次只切一刀把立方体分成两部分,比如第一次沿 x 轴切,分成两部分,下一次在两个区域中沿 y 轴切,再下一次每个区域都沿 z 轴切,这样每次都只把一个区域分成两块,且划分方向交替进行,也保证了相对均衡,因此在图形学中KD树更为合适
- BSP树类似于KD树,只是划分方向可以是任意方向,但因为我们图形学中用的是轴对齐包围盒所以这种方法不适用
接下来我们按照上面说的KD树的思路我们来看KD树是如何工作的。
首先是构造KD树,我们先把一个场景划分一次,形成两个子区域:
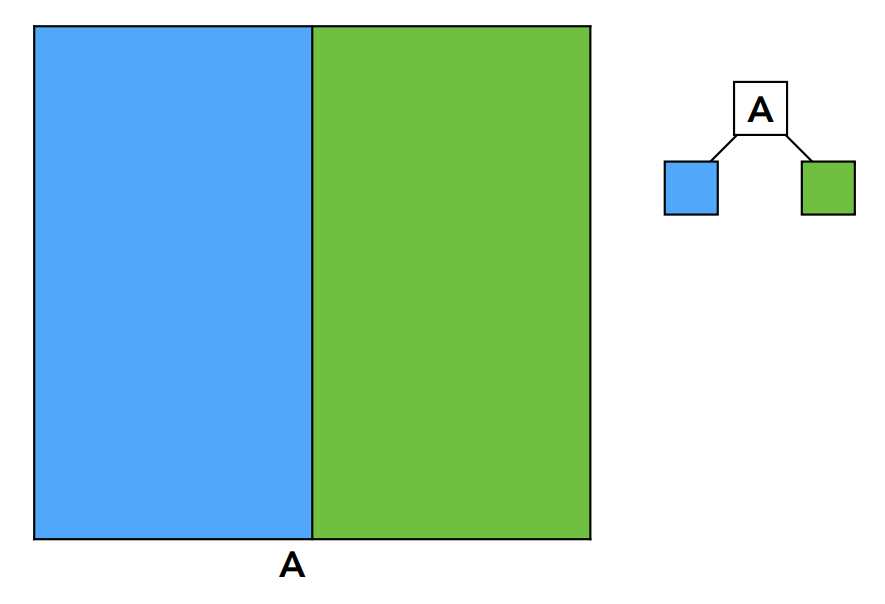
然后对每个子区域继续划分又分别得到两个子区域,这里我们只划分了绿色的子区域,实际上蓝色的也应该继续划分:
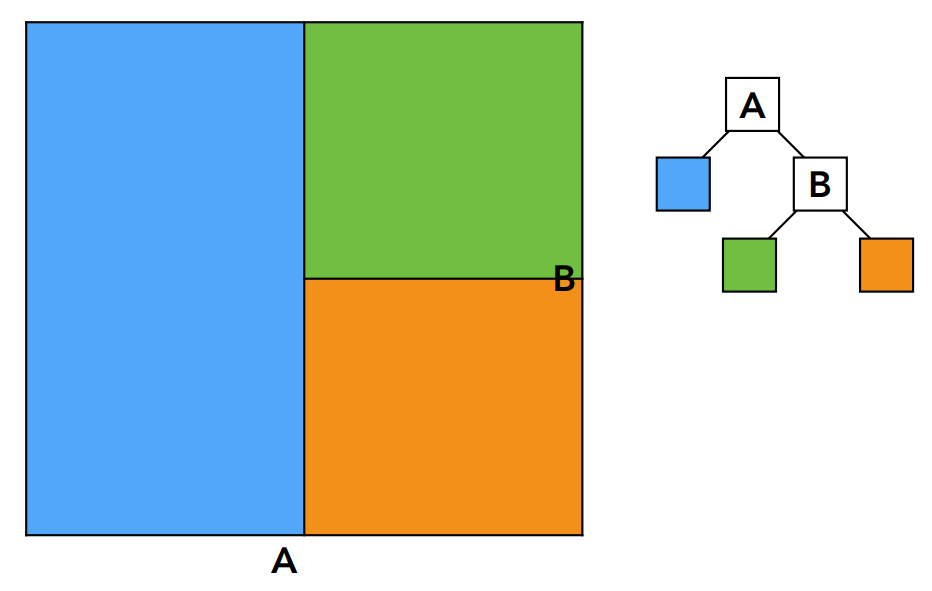
然后继续划分:
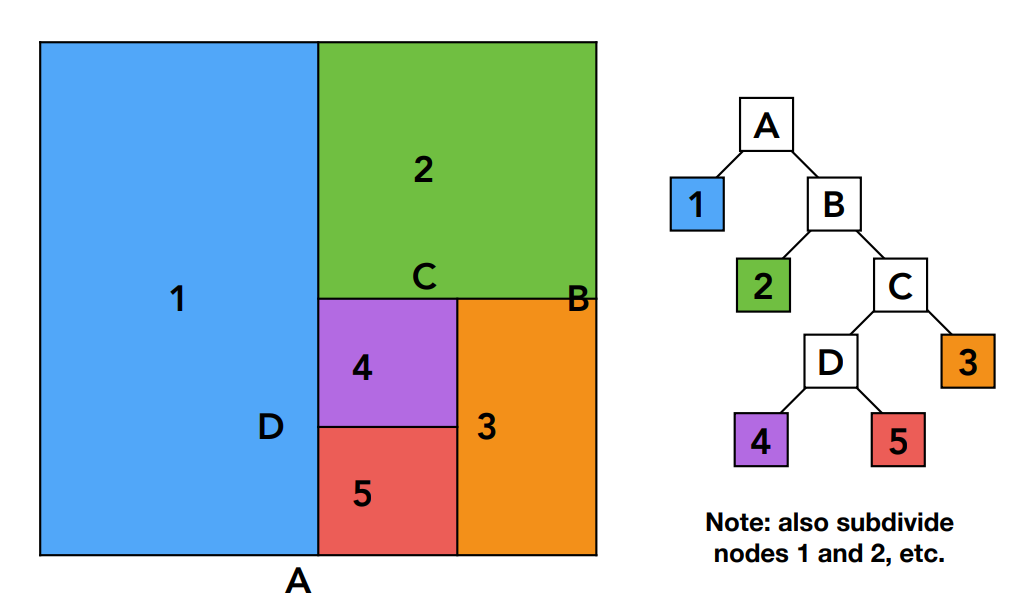
这样我们得到了一个KD树,KD树中的节点分为两类:
- 中间节点:代表一个大区域,中间节点不存储物体信息,只存储这个区域下一次的划分方向(沿 x,y,z轴),划分的位置(这里都是从中间划分,实际可以根据物体位置计算划分位置)以及孩子节点
- 叶子节点:叶子节点存储在这个区域中所有的物体列表
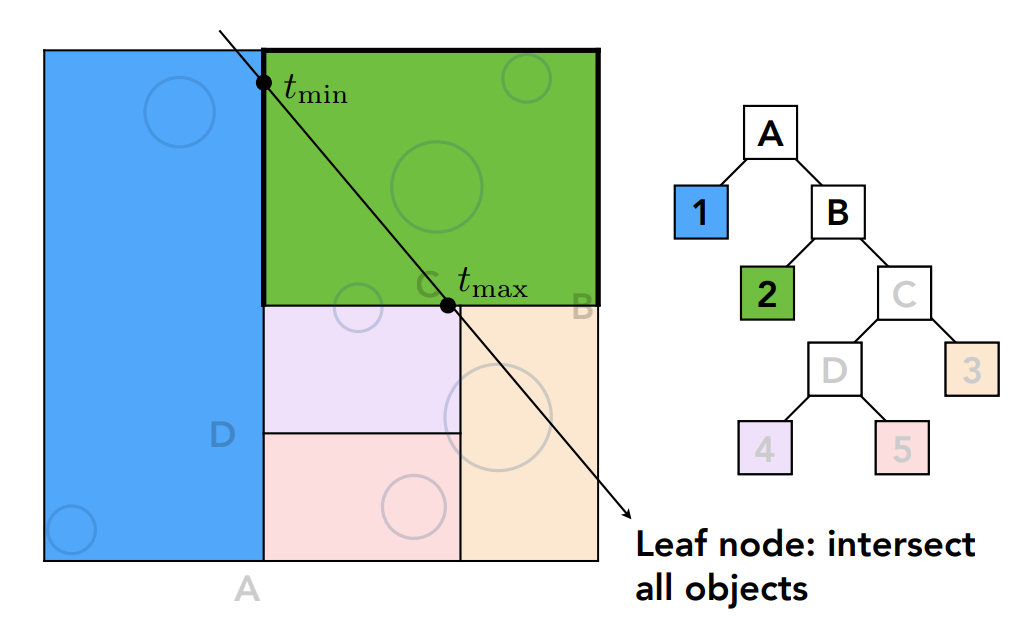
当我们预处理好了一个场景的 KD 树,在进行光线追踪时,每一条光线射入场景,先从 KD 树的根节点开始计算:
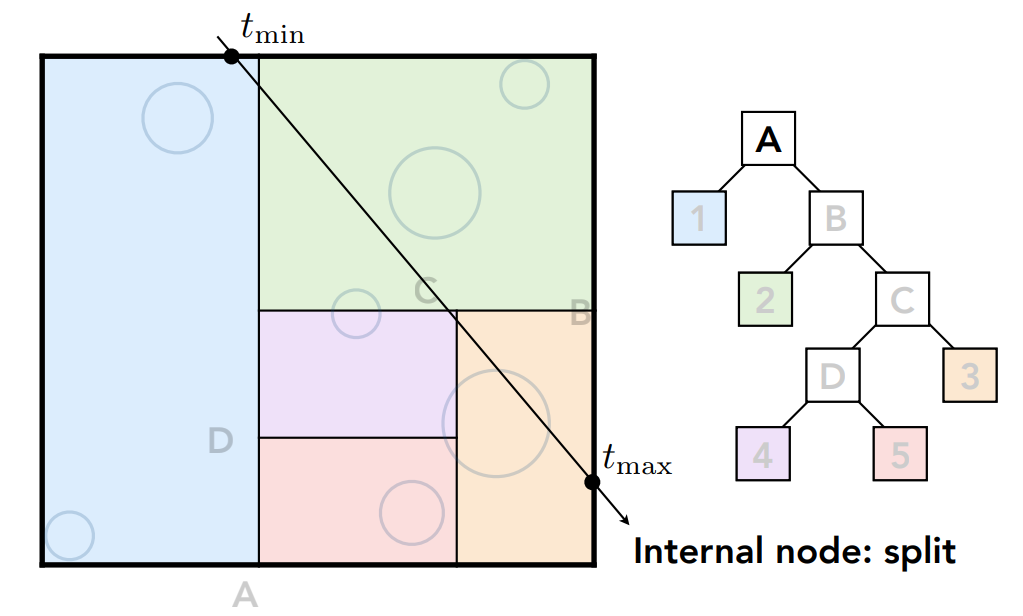
得到光线和区域 A 有交点,那么开始遍历它的孩子节点,计算和蓝色区域的相交情况:
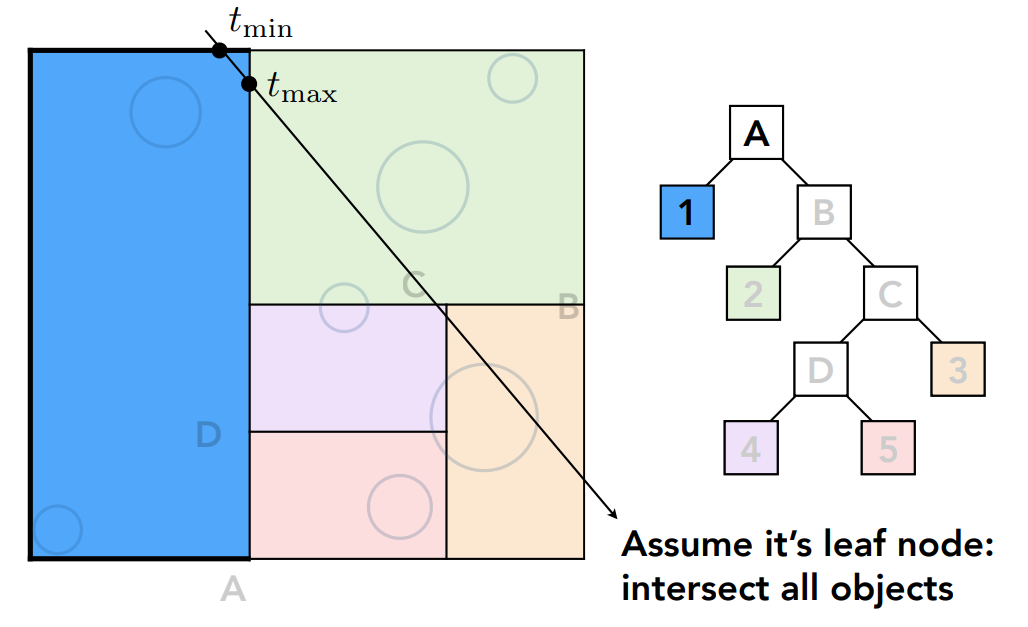
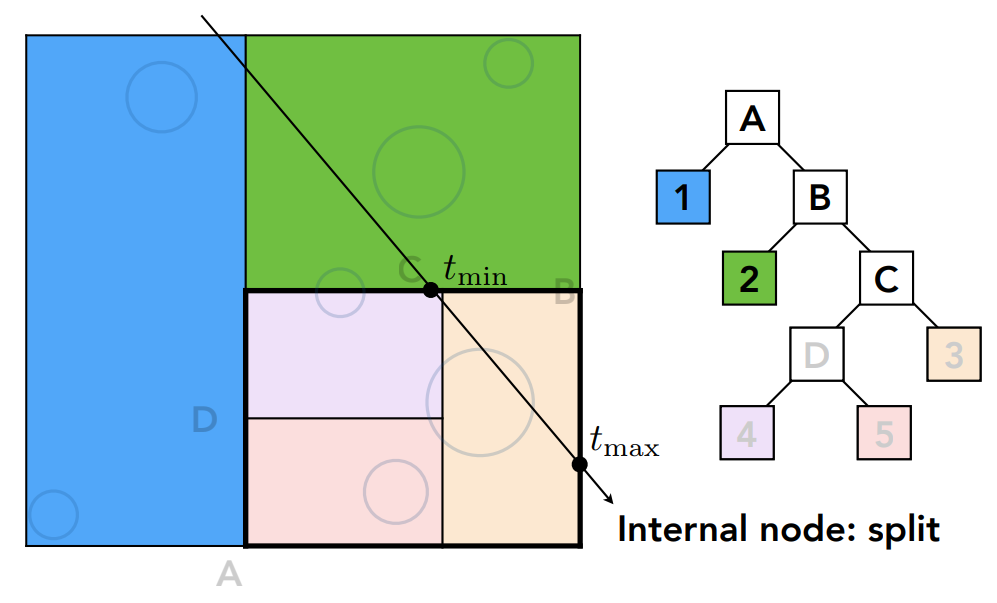
也有交点,并且这是一个叶子节点,那就计算光线这个区域中所有的物体的交点,然后继续计算和 B 区域的交点:
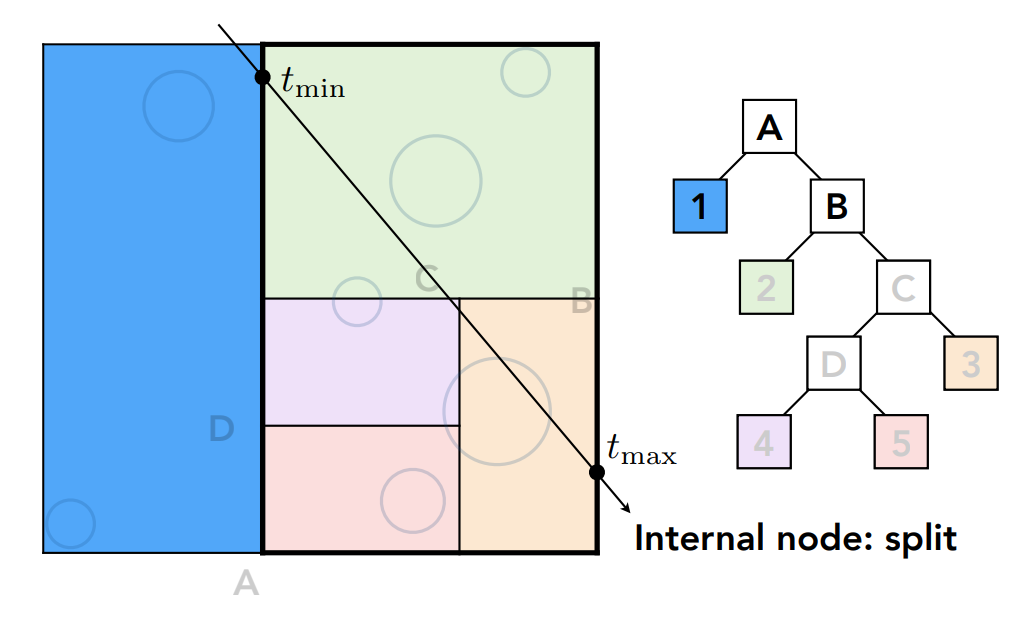
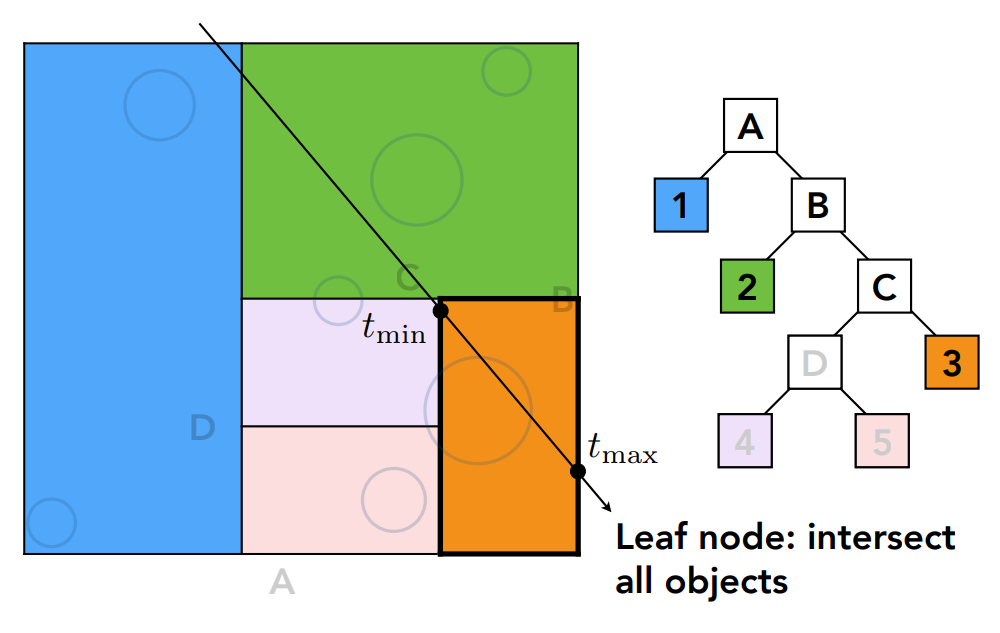
存在交点继续遍历:
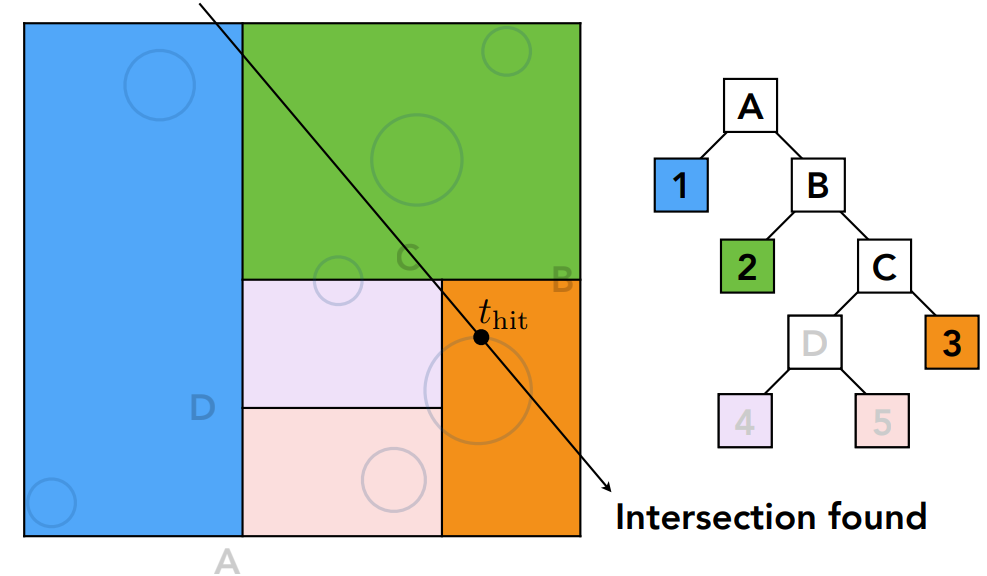
直到找到和物体的最近的交点,当然这只是一个示例情况,光线和所有区域都相交,实际过程中KD树显然可以大幅降低光线和立方体判断交点的次数,自然也就进一步降低了和三角形计算交点的次数。
但是 KD 树也存在缺陷,每个叶子节点要存储在这个区域内的所有物体,那么如何判断一个物体在这个立方体中呢?这是非常困难的,但也不是不能克服,不过还有一个问题就像上图所示,有的物体会同时在好几个区域中,那么这几个区域的叶子节点就都要存储这个物体的信息,会有大量重复,因此 KD 树不是最好的划分方法。
4.4 物体划分和BVH(Bounding Volume Hierarchy)
最好的办法就是不对空间进行划分,而是对空间中的所有物体进行划分,类似于KD树,我们把空间中所有物体的 Bounding Box 找到,作为根节点:
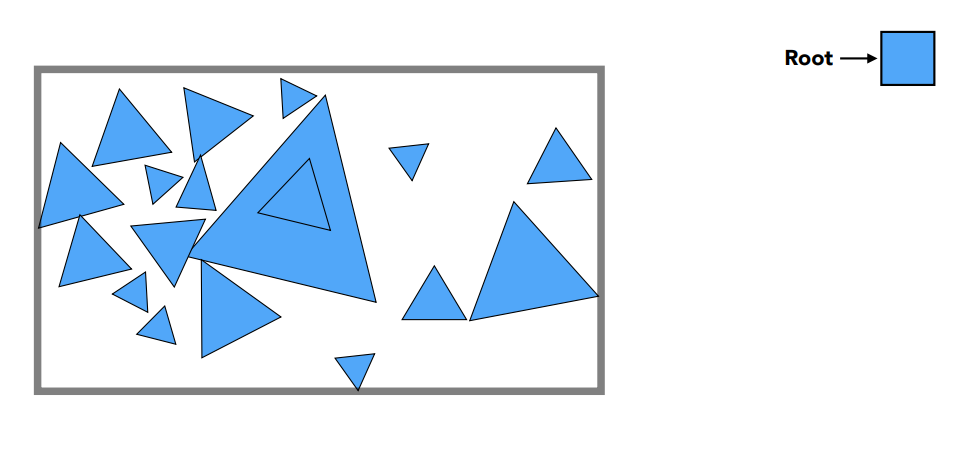
然后把物体分成两堆,并且重新计算这两堆物体的 Bounding Box :
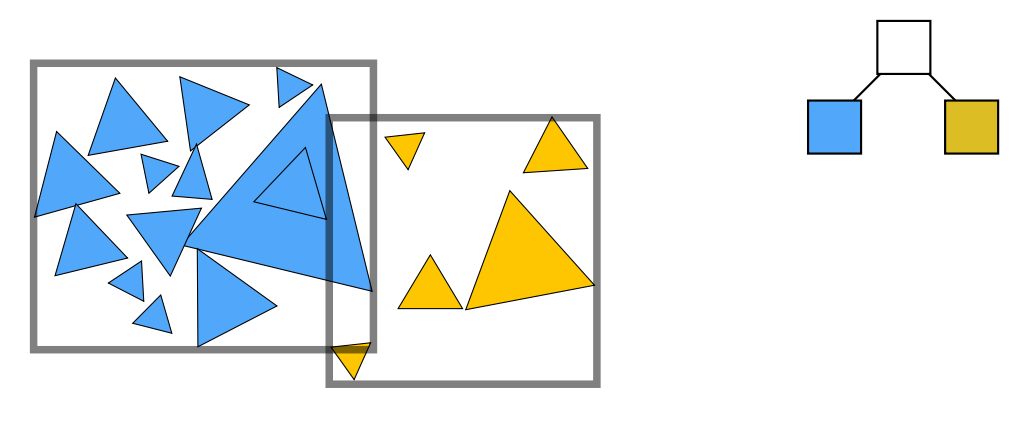
接下来继续这个过程,直到每个区域中都有我们希望的数量的物体:
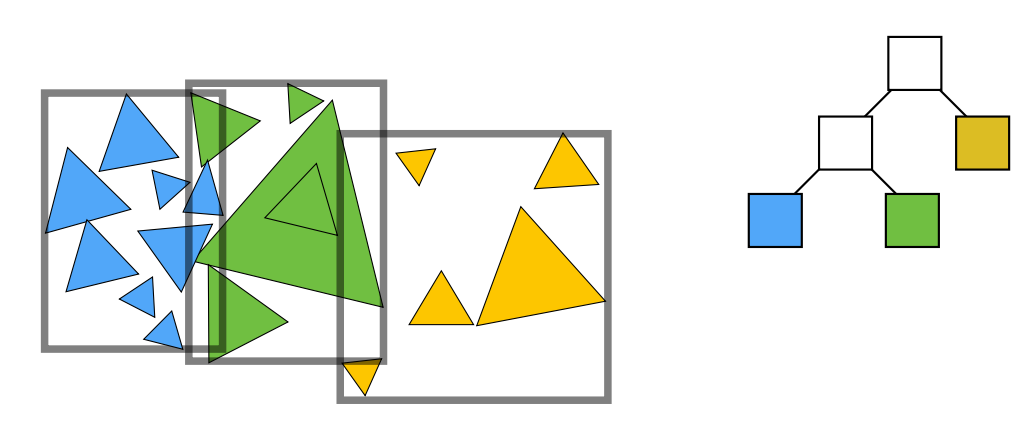
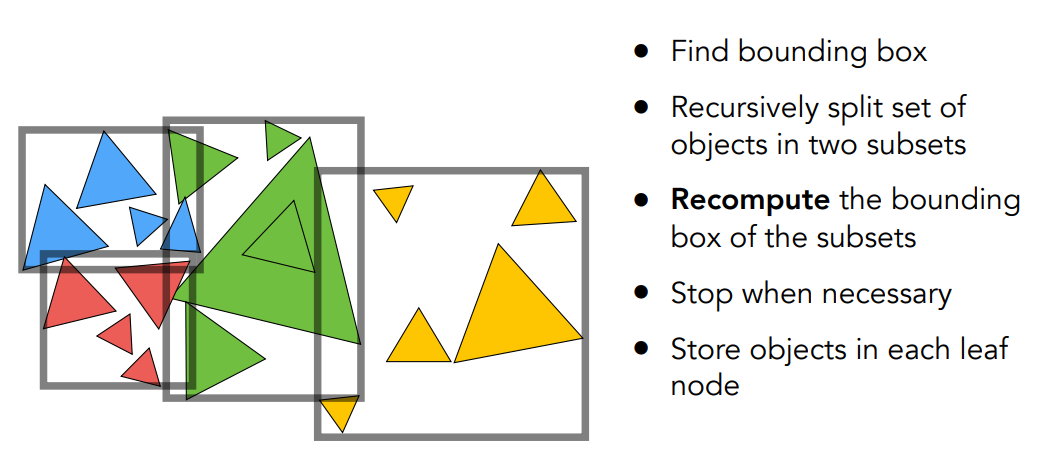
可以看到 BVH 构建过程和 KD 树类似,只是每次划分是对物体进行划分然后重新计算 Bounding Box ,这样就可以保证每个叶子节点存储的物体不重复,并且还免去了判断物体是否在 Bounding Box 内的麻烦,是一个非常优秀的方法,因此 BVH 也是目前使用最广泛的方法。
至于每次对物体如何划分,当然可以和 KD 树一样按照维度轮换划分,也可以用其他各种方法,比如:
- 永远选择最长的那一个维度划分,有时可能场景是一个走廊之类的长条形状,那么其中的物体也一定是按这样排列的,如果还按照维度轮换划分,划分出来一定是不够均衡的,因此可以每次计算当前 Bounding Box 最长的那一维,就从最长维度划分,就可以保证相对均匀
- 可以选择中间的物体划分,为了保证每个叶子节点存储的物体数量差不多,我们可以把物体的中心坐标排序取中位数,然后按照中间这个物体所在位置划分成两个区域,这样每个区域中物体数量都相当
BVH 的数据结构中存储的内容和 KD 树类似,中间节点存储 Bounding Box 和孩子节点,叶子节点中存储 Bounding Box 和所有物体列表,当光线射入场景时,从根节点开始计算即可,下面是 BVH 的伪代码:
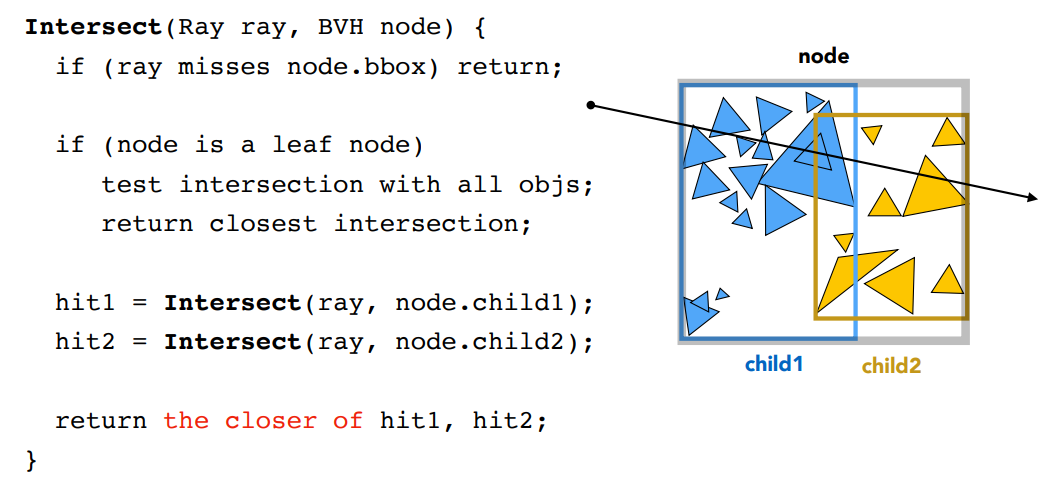
4.5 空间划分 VS 物体划分
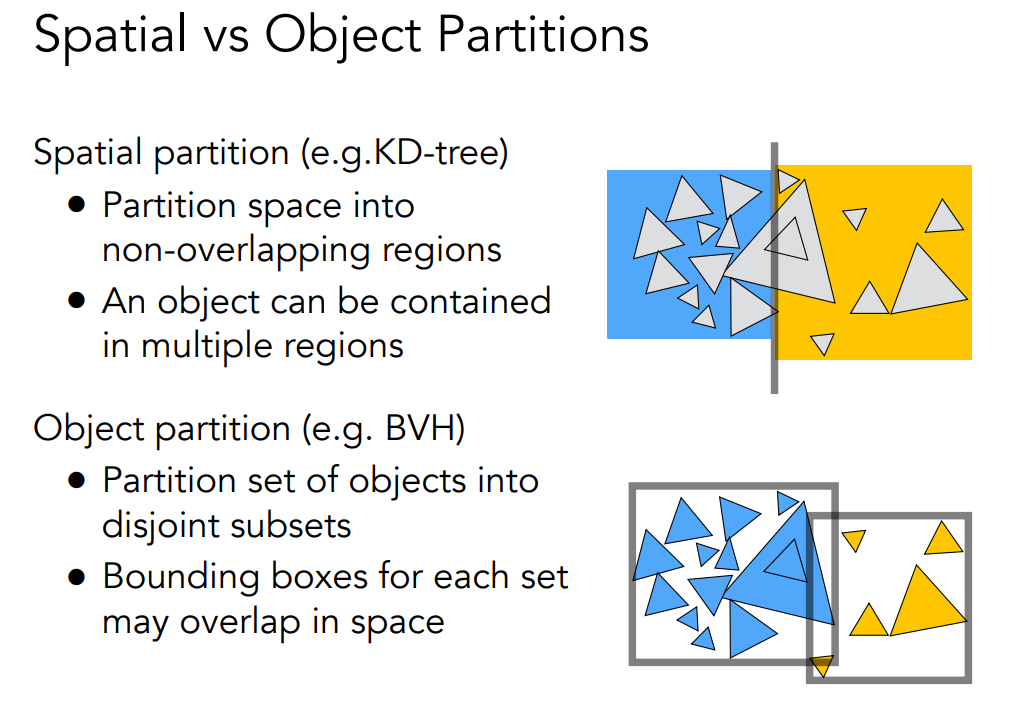
对比 KD 树和 BVH,一个是空间划分,一个是物体划分,空间划分的 Bounding Box 不会重合但是物体会重复,而物体划分 Bounding Box 可能重合但物体不会重复,显然物体划分更符合我们的需求。
5 总结
以上就是 Whitted 风格光线追踪的基本原理和优化结构,从每个像素投射一条视线到场景中,利用 BVH 找到和场景中物体最近的交点,然后利用同样的方法计算反射和折射光线与其他物体的交点,最后计算所有交点的着色作为这个像素的颜色显示。