几何(Geometry)
图形学中几何是最最重要的部分之一,但同时也是极其复杂的一个课题,这一节只是对计算机图形学中几何的一些最基本的概念、算法做介绍,更加深入的图形学几何知识我们之后再去涉及。这部分内容主要包括几何的表示方式、贝塞尔曲线、分段贝塞尔曲线、B样条、贝塞尔曲面、曲面细分的几种算法和曲面简化的基本原理。
1 几何表示方法
几何讨论的实际上就是计算机中如何去描述曲线或者曲面这样的几何图形,比如下图这样复杂的曲线:

再比如:

这样复杂的物体我们几乎不可能通过建模去完成,因此需要一些方法对几何进行有效的表示。
几何表示方法大体分为两大类,隐式表示和显式表示。
隐式表示是指我们无法通过通过给定的表示方法直接知道它表示的是什么图形或者什么物体,比如我们非常熟悉的代数方程,给出一个方程我们无法直接知道这个方程表示的是什么,也很难知道哪些点在这个方程表示的物体上,如下图:
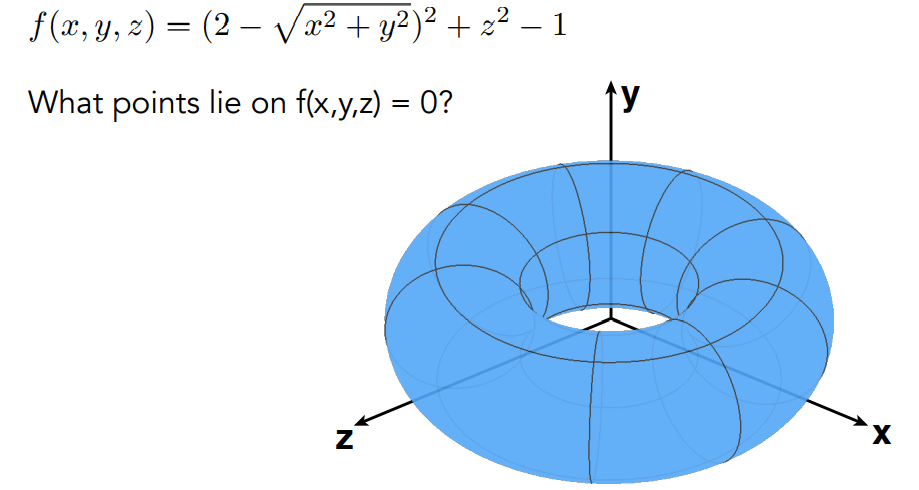
只根据这个代数方程我们很难知道哪些点在这个物体上,但是给定任意一个点,我们根据方程可以很容易的判断它是否在这个物体上,或者在这个物体内部还是外部。
而显式表示是指直接给定这个几何图形上的所有点,或者给定一种参数映射规则,根据规则我们可以很容易得出哪些点在这个几何物体上,比如:
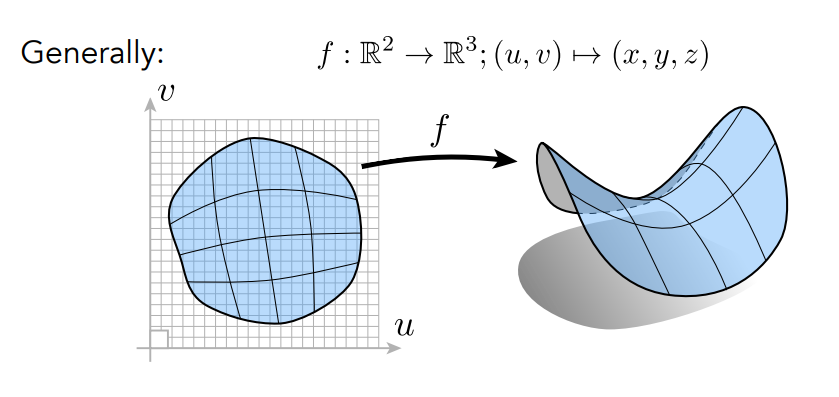
我们可以把二维上的点通过某种规则映射到三维形成我们要表示物体,此时我们只需要根据规则把二维坐标带入就可以得到三维物体上每一个点的坐标了,对于刚才的例子,它的一种显式表示如下:
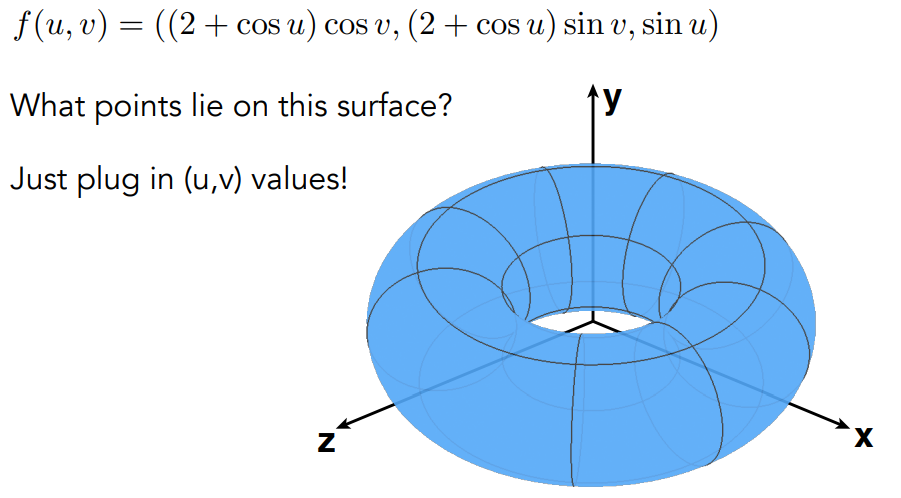
我们只需要把某个范围内的二维坐标带入,就可以得到这个物体上每个点的三维坐标了。但是如果我们想要判断某个点是否在物体上,或者在物体的内部还是外部的时候,显式表示就没有很便捷方法能够做这样的判断了。
因此,隐式表示和显式表示各有优劣,在实际任务中使用什么样的表示,完全取决于我们的需求,根据不同的需求选择具有不同特性的表示方法,再利用这种表示完成我们想要的效果,这也正是几何之所以非常困难的原因。
接下来分别简单介绍几种隐式表示和显式表示方法。
1.1 一些隐式表示方法
- 代数表示:最常见的隐式表示方法,但是表示特别复杂的物体时会非常困难

- 构造实体几何(Constructive Solid Geometry):通过对一些基本几何图形进行运算操作,比如交、并、差等操作,得到复杂的几何图形
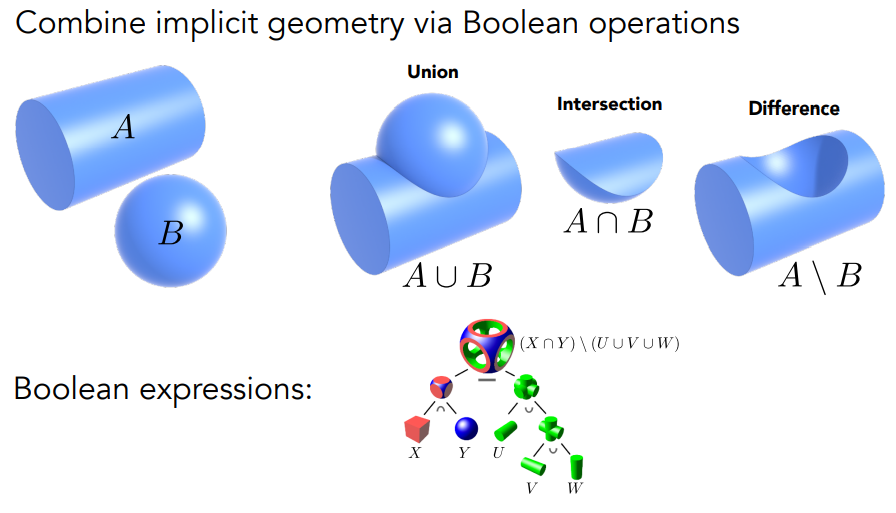
- 距离函数(Distance Functions):距离函数是隐式表示中非常强大的一种表示方式,所谓距离函数是指通过定义空间中任何一个点到离它最近的物体表面的距离,来定义一个物体。这样做的好处是便于不同物体之间的融合,如下图:

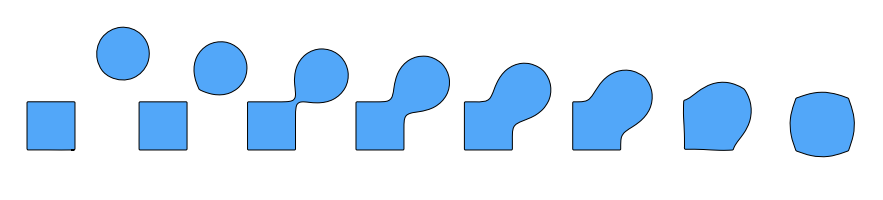
两个小球的融合如果用上面的一些表示方法是没有办法表示的这么平滑的,但是距离函数可以做到。我们可以先把两个小球用距离函数表示,然后把它们的距离函数做一个融合,融合之后的新的距离函数还原为模型,就得到了平滑的融合模型。融合的过程如下图:
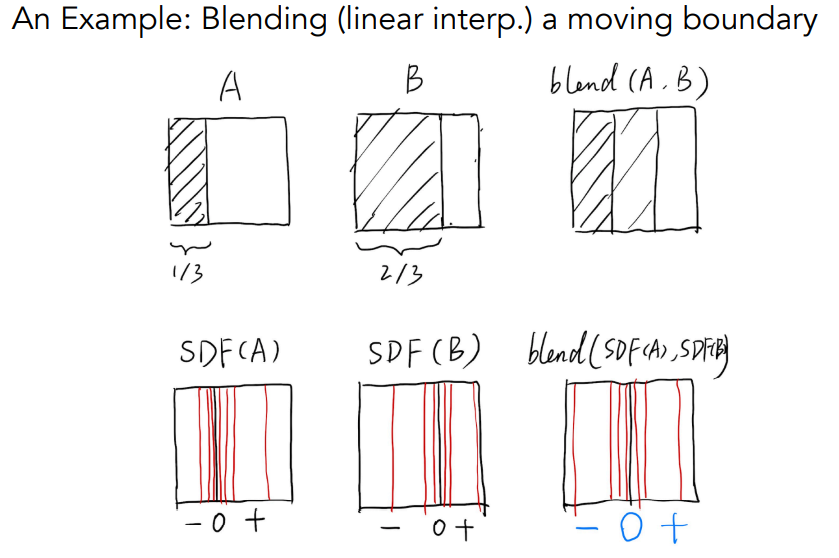
A和B中阴影部分都代表某一个物体,阴影和空白的分界线自然就是这个物体的表面,因为距离函数的定义是空间中任意一点到离它最近的物体表面的距离,因此所谓两个物体的融合,其实也是两个物体表面的融合。根据距离函数的定义,A 和 B 的距离函数就是下面的 SDF(A) 和 SDF(B) 所示的样子,“o“ 代表距离为0,也就是这个物体的表面,那么当这两个距离函数融合之后,A的距离函数原本应该取正值的部分(表面的右边),会和 B 的距离函数原本取负值的部分(表面的左边)叠加起来,这样就会形成一个新的 0 平面,这个新的 0 平面就是两个物体融合后新的表面,再还原为物体自然就得到了平滑融合后的新的物体。
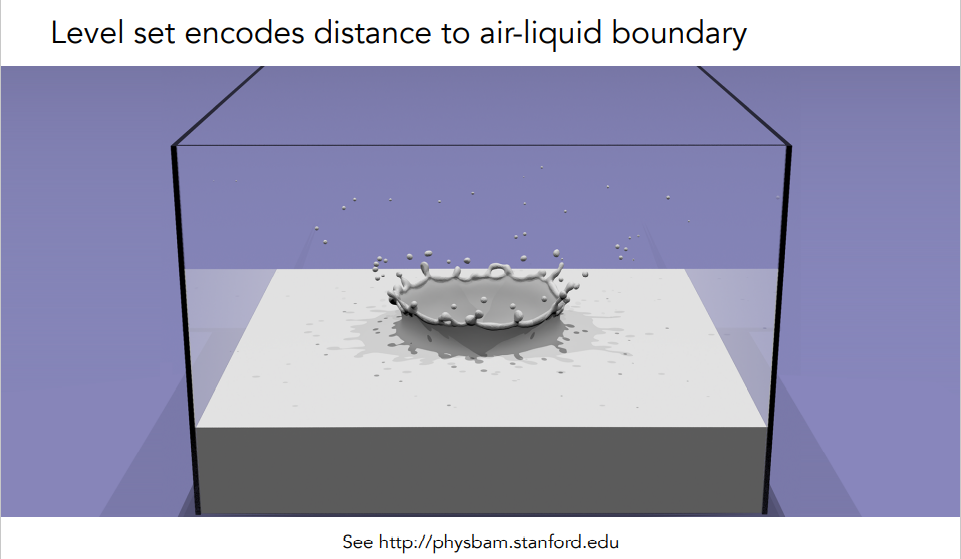
- 水平集(Level Set):水平集也是在图像分割领域广泛应用的一种隐式表示方法,比如下图中水的涟漪就是用水平集建模表示的。
- 自相似(Fractals):自相似就是用自身组成自身,类似于递归

最后总结一下隐式表示的优缺点:
优点是隐式表示对简单的物体能够表示的非常准确,并且容易做内外侧的判断,也便于光线与表面关系的计算,还可以很容易的进行拓扑变换,比如流体的模拟。但缺点也很明显就是很难去对复杂的模型进行表示。
1.2 一些显式表示方法
- 点云(Point Cloud):最直接的显式表示方法,可以很容易地表示任何几何图形,因此目前也应用广泛。
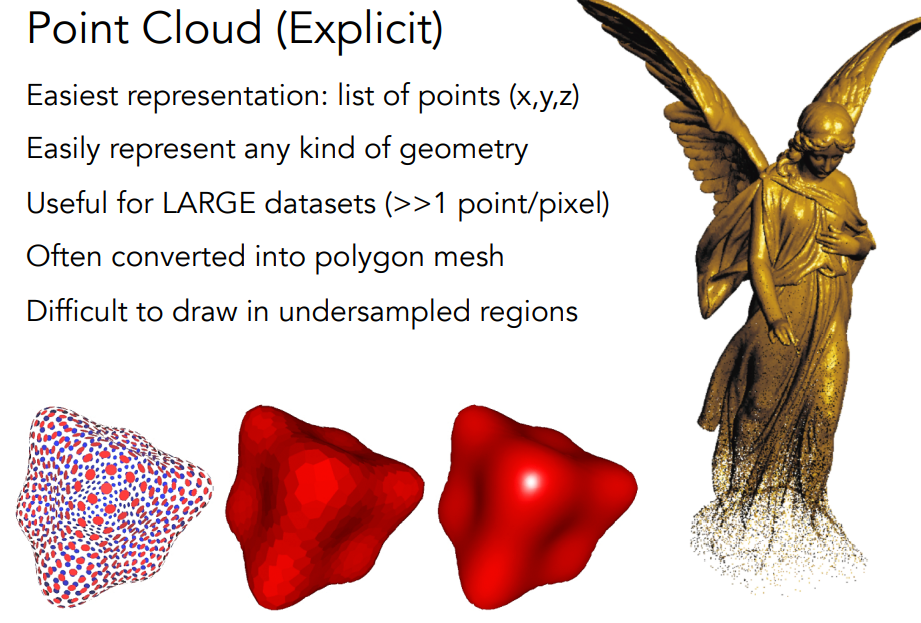
- 几何片面(Polygon Mesh):图形学中使用最广泛的表示方式,也就是我们之前接触到的用三角形或者四边形片面组成一个模型:

提供给我们的是模型上每一个片面的顶点以及它的一些属性(纹理坐标、法向量等等),还有这些顶点的组合方式,哪几个顶点组成一个片面。下面是一个模型文件(.obj)的内容:
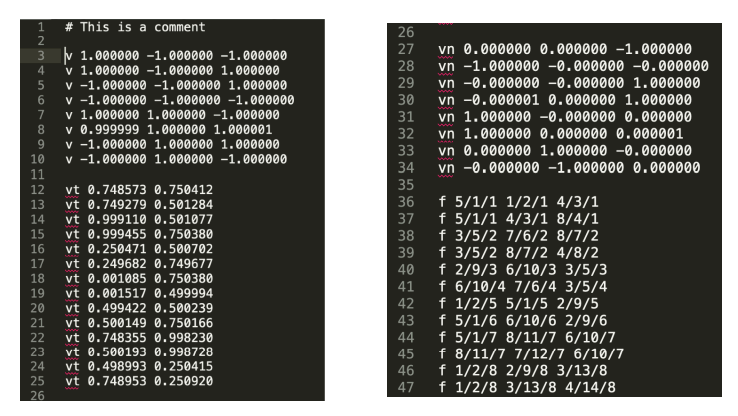
其中 v就是顶点坐标,vt 是纹理坐标,vn 是法向量, f 是顶点组合方式,比如第36行的组合方式表示用第 5 个、第 1 个和第 4 个顶点组成一个三角形,三个顶点分别使用第 1 个、第 2 个、第 3 个纹理坐标,都使用第 1 个平面的法向量。
了解了几何的表示方式,我们接下来开始具体讨论曲线和曲面。
2 曲线
曲线在图形学中非常重要,比如动画中摄像机的运动轨迹,我们运镜时要先定义好一个曲线,然后让相机在这个曲线上运动来拍出我们想要的效果;或者空间中一个物体运动的轨迹,我们也要事先把这个轨迹定义好。因此我们就需要有一种方法能够表示空间中任意形状的曲线,图形学中最基本的曲线表示方法就是贝塞尔曲线(Bézier Curves)。
2.1 贝塞尔曲线(Bézier Curves)
贝塞尔曲线就是根据给定的控制点去唯一的确定一条曲线,比如下图所示的贝塞尔曲线,给定了四个控制点 $p_0$ 、 $p_1$ 、 $p_2$ 、 $p_3$
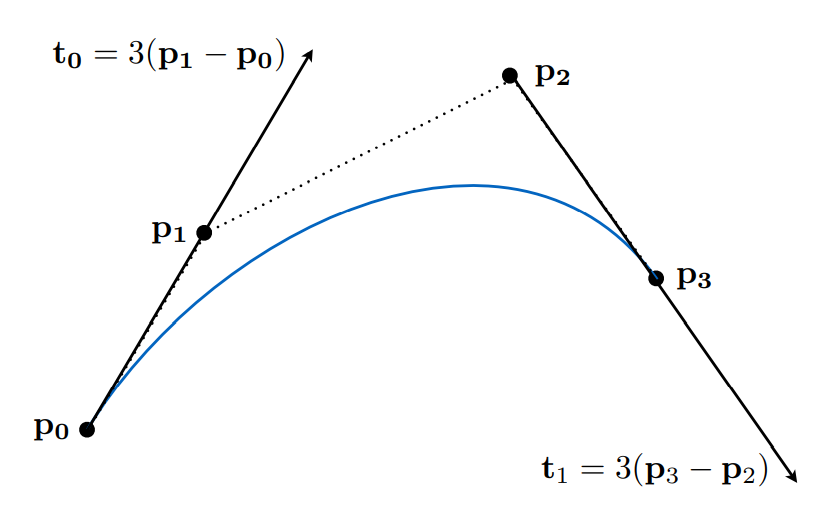
那么所确定的这条曲线要满足几个条件:
- 过第一个和最后一个控制点
- 曲线起始的切线方向沿 $\vec {p_1 p_0}$ 方向
- 曲线末尾的切线方向沿 $\vec {p_3 p_2}$ 方向
这样就确定出了一条贝塞尔曲线。那么我们怎么样快速的根据给定的控制点确定一条贝塞尔曲线呢?
2.2 de Casteljau 算法
de Casteljau 算法用来根据给定的控制点得到曲线上的点。首先我们先考虑三个控制点的情况,此时的贝塞尔曲线称为二阶贝塞尔曲线:
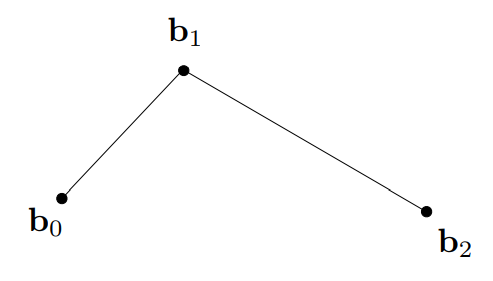
对于给定的三个控制点 $b_0$、$b_1$、$b_2$,我们将他们相邻的两两连接起来形成两条线段,假设在线段 $b_0 b_1$ 上 有一个点 $b_0^1$ 在沿着线段移动,那么这个点会把线段分为两个部分,如下图:
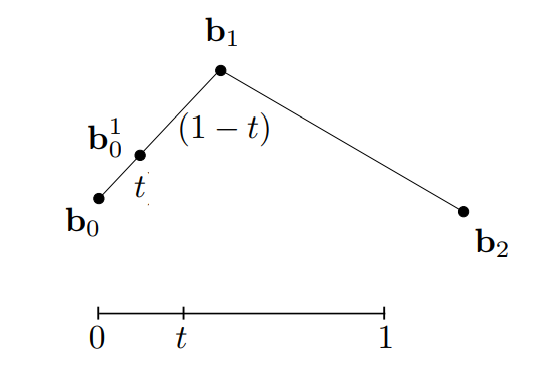
假设线段长度为 1,那么我们可以用一个在 0 到 1 之间的系数 t 来表示点 $b_0^1$ 在线段上移动了多少,也可以理解为 t 这个时刻点 $b_0^1$ 在线段上的位置,同样我们在线段 $b_1 b_2$ 上找一个 点 $b_1^1$ ,也移动了 t 距离:
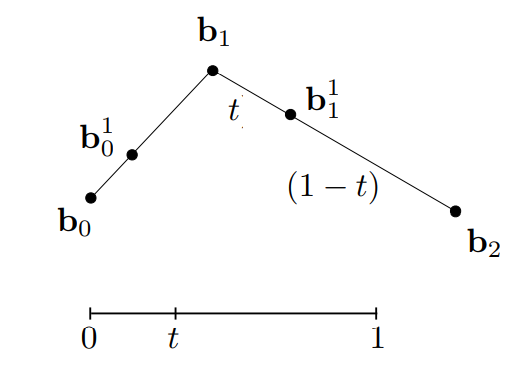
然后连接这两个点形成线段 $b_0^1 b_1^1$,然后在这条线段上继续寻找移动了 t 距离的点 $b_0^2$
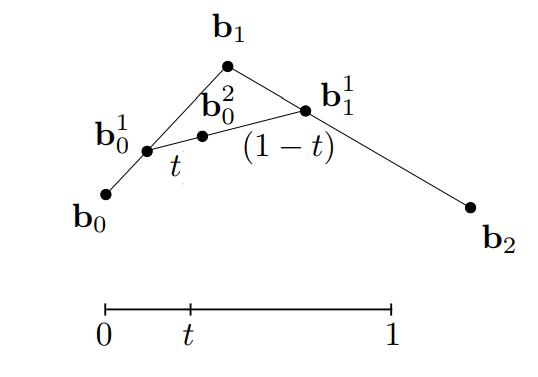
此时这个点无法再形成线段,那么这个点就是由这三个控制点形成的曲线上在 t 时刻的点:
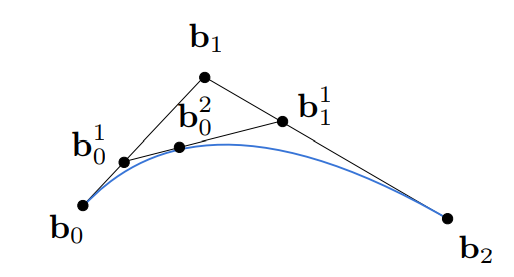
于是对于任意一个 $t \in [0,1]$,都可以确定一个曲线上的点,这相当于定义了一种参数转换规则来描述这个曲线,因此贝塞尔曲线是一种显示的几何表示方法。
那么同样对于三阶贝塞尔曲线,有四个控制点,按照同样的方法就可以得到曲线上的点了:
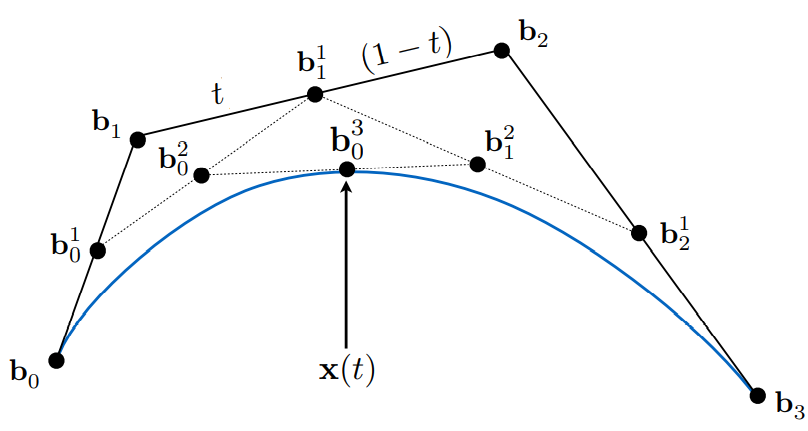
下面的动图很好地展示了这一过程(来自Making things with Maths (acko.net)):
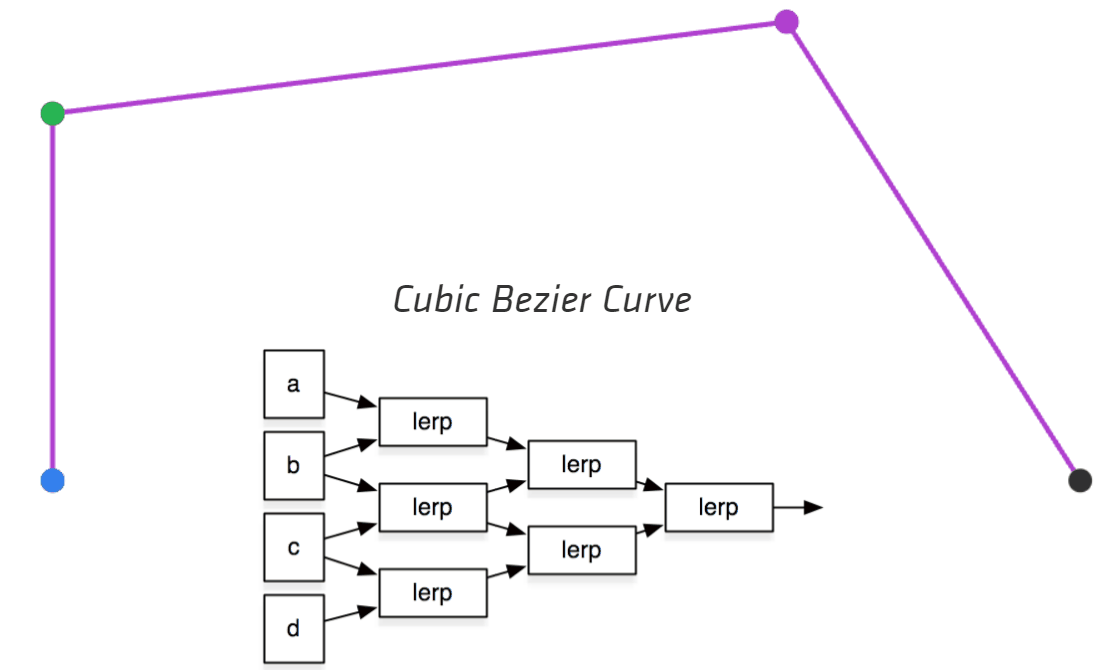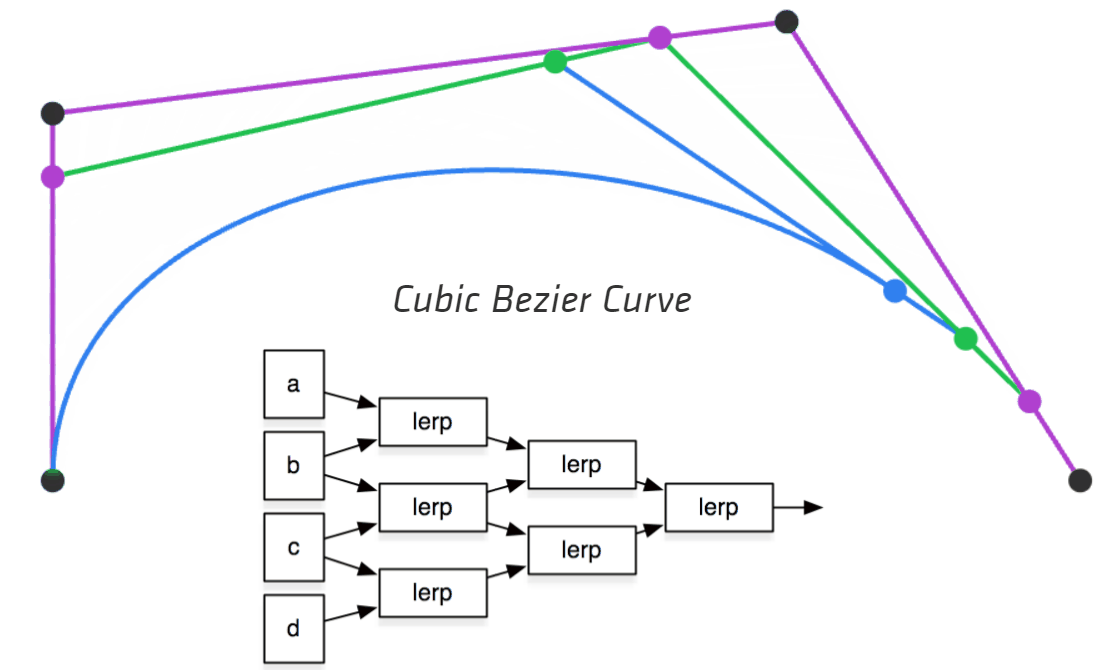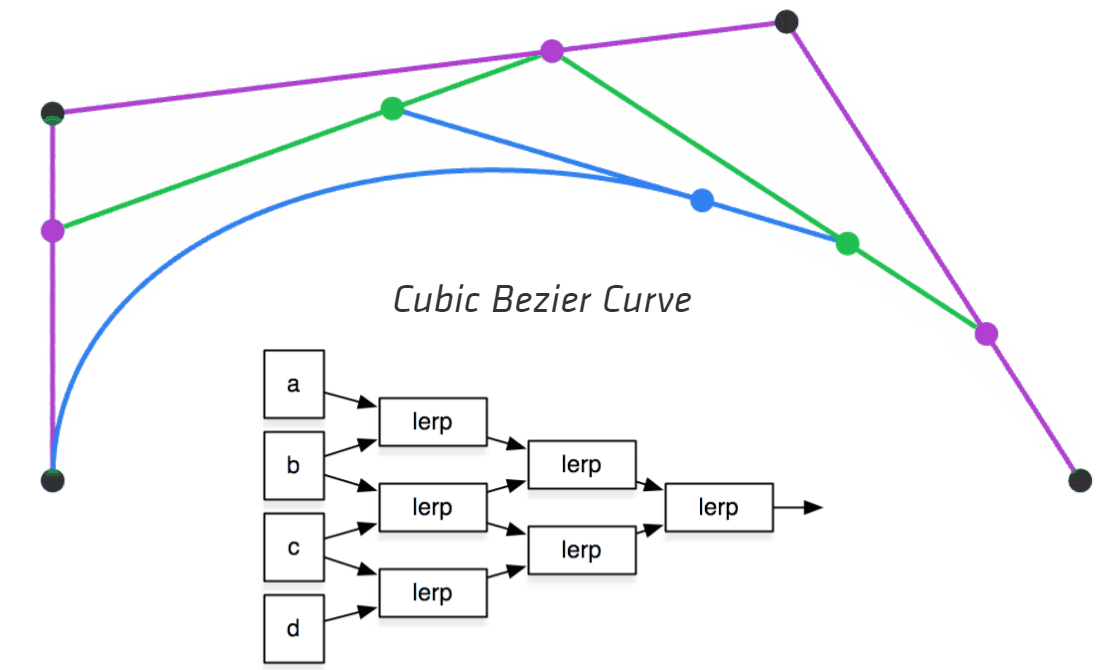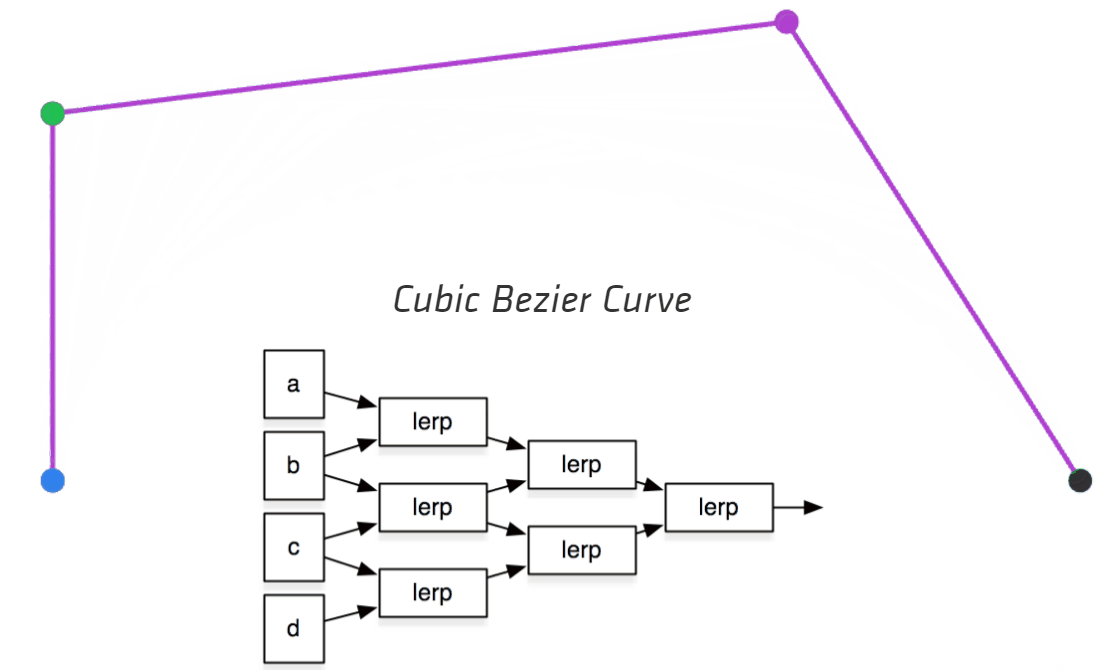
2.3 贝塞尔曲线的代数表示
实际上通过de Casteljau 算法,我们可以很容易写出贝塞尔曲线的代数表示:
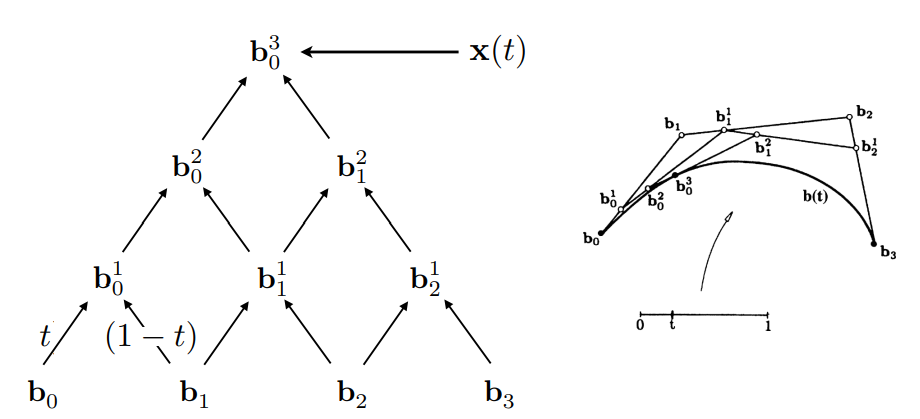
每一个中间点都相当于线段两个端点做了一次线性插值,直到最终得到一个点,这个点就是曲线上的点。再以刚才的二阶贝塞尔曲线为例:
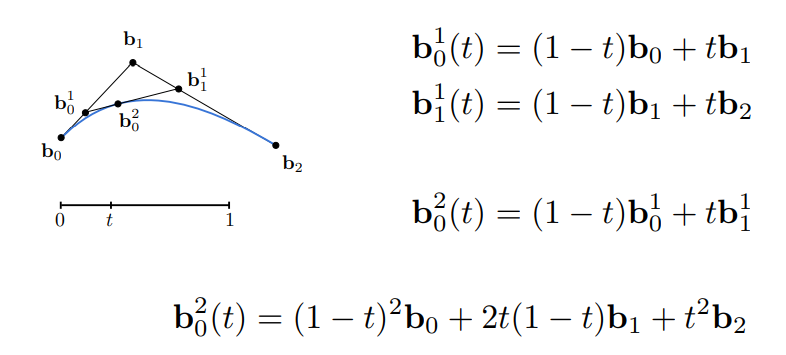
可以看到 $b_0^2$ 的表达式系数就是一个完全平方展开,刚好是 $[(1-t) + t]^2$ 的展开,也就相当于 1 的二阶展开项。
那么我们可以写出贝塞尔曲线的一般形式:

对于 n 阶贝塞尔曲线上的点,实际上是就是所有 n + 1 个控制点的加权和,加权系数是伯恩斯坦多项式,其实就是二项式系数。
比如对于一个三阶贝塞尔曲线,我们给定了 4 个控制点的坐标,那么根据伯恩斯坦多项式就可以确定出曲线上的点的坐标满足的关系:
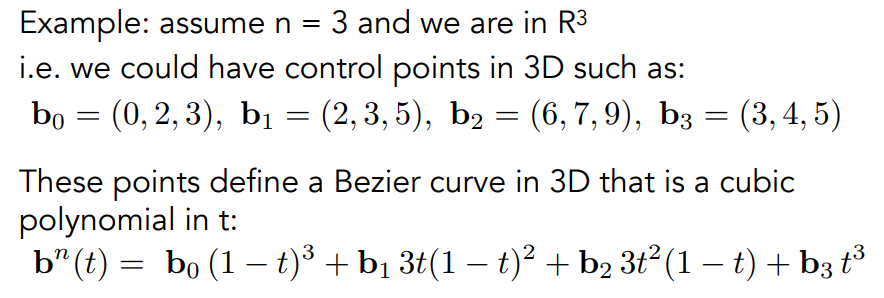
关于伯恩斯坦多项式,实际上就是 1 的 n 阶展开,如下图:
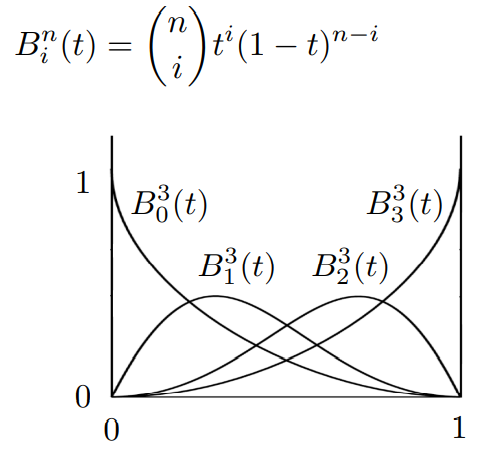
在任意时刻 t,各阶伯恩斯坦多项式的值和都为 1 .
2.4 贝塞尔曲线的性质
贝塞尔曲线有如下的一些性质,以三阶贝塞尔曲线为例:
- 过第一个和最后一个控制点:
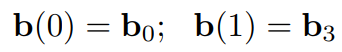
- 切线方向:这里的系数 3 是因为我们是三阶贝塞尔曲线,更高阶的系数就不一定是 3 了
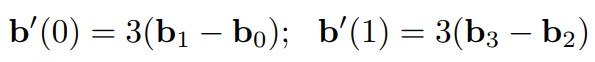
- 仿射不变性:一条贝塞尔曲线经过任意仿射变换相当于控制点经过任意仿射变换,因此我们要对贝塞尔曲线进行仿射变换无需对去线上的所有点变换,只要对控制点变换即可,但只有仿射变换满足这个性质,投影变换不满足
- 凸包性:贝塞尔曲线一定在所有控制点形成的凸包内,所谓凸包就是能涵盖所有点的最小凸多边形,如下图:
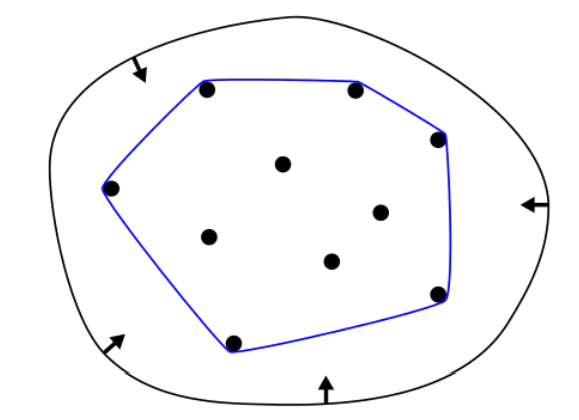
2.5 分段贝塞尔曲线(Piecewise Bézier Curves)
贝塞尔曲线也有一定的缺点,比如对于一个 10 阶贝塞尔曲线:
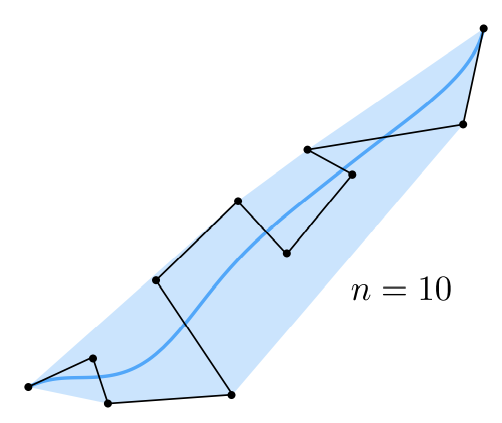
可以看到这个曲线并没有想象中那么扭曲,而是相对平缓,这是因为高阶的贝塞尔曲线我们很难通过控制点去改变曲线的形状,因此人们发明了分段贝塞尔曲线。
既然高阶不好控制,那我们可以把曲线分段,每一段用一个低阶的贝塞尔曲线(通常就是 3 阶)表示,最后再把他们连接起来,就可以形成各种复杂的曲线了。

这里还有一个demo网页可以帮助我们理解分段贝塞尔曲线,可以通过拖动每一个控制点改变曲线。
那既然曲线连接起来了,就存在一个问题,就是两段曲线之间的连续性,比如上图中就有很多尖点显然是不连续的,但实际工程中我们希望很多复杂的曲线要严格连续,因此要定义两个贝塞尔曲线的连续性。
- $C^0$ 连续:前一段曲线的最后一个控制点就是后一段曲线的第一个控制点,就称两条曲线满足 $C^0$ 连续
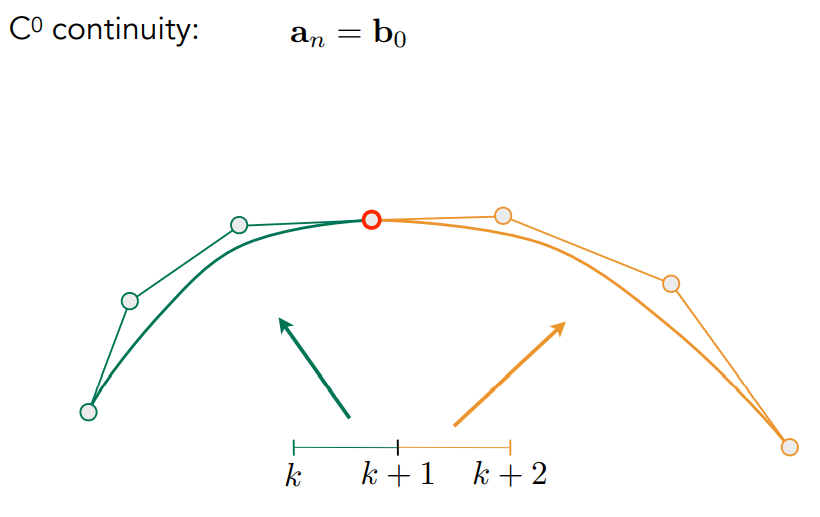
- $C^1$ 连续:两段曲线的连接点是两条曲线倒数第二个控制点和第二个控制点连线的中点,实际上就是第一段曲线结尾的切线方向和第二段曲线开始的切线方向相同,也就是一阶导数严格相等。
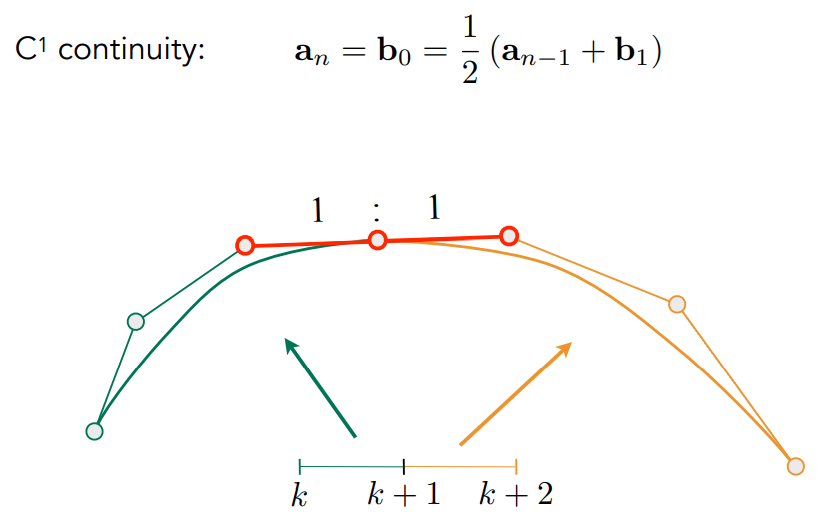
虽然许多时候 $C^1$ 连续已经能满足我们的要求,但有些时候我们需要更严格连续,这时就要满足 $C^2$ 或者更高阶的连续,也就是二阶导数或者更高阶导数相等。
2.6 B样条(B-splines)
通过上面对贝塞尔曲线的了解,我们发现贝塞尔曲线有两个关键的缺点:一是改变任何一个控制点的位置,会对整条曲线产生影响,但很多时候我们并不希望如此,我们只希望在局部改变曲线形状,当然这可以由分段贝塞尔曲线来解决;另一方面就是虽然分段贝塞尔曲线能够解决局部性问题,但是改变了某一段的贝塞尔曲线,就可能会影响和这条曲线相连接的部分的曲线连续性,可能会导致曲线连续性降低。B样条就可以完美地解决这两个问题。
B样条实际上是贝塞尔曲线的一般化,简单来说样条就是指由一组控制点控制的曲线,B样条是 basis splines 的缩写,也就是由basis函数组成的样条,basis函数就是基函数,因此B样条就是由一组基函数表示的样条曲线。
对于给定的 n + 1 个控制点,贝塞尔曲线一定是 n 阶的,但是B样条并非如此,因此B样条相比于贝塞尔曲线更加灵活。具体来说,B样条可以把一个控制点的改变对于曲线形状的影响控制在一定范围内,这样就方便我们去做局部的调整了。并且B样条天然具备高阶连续性,且不必定义在固定区间 [0,1] 上,这给曲线的表征带来了极大的方便。
但是B样条无法表示一些基本曲线,比如圆,因此又引入了非均匀有理B样条(NURBS),具体关于B样条的内容可以查看本篇的更多部分内容。
3 曲面
3.1 贝塞尔曲面(Bézier Surface)
把贝塞尔曲线推广到三维,就是贝塞尔曲面,因此贝塞尔曲面同样是显式的几何表示方法。
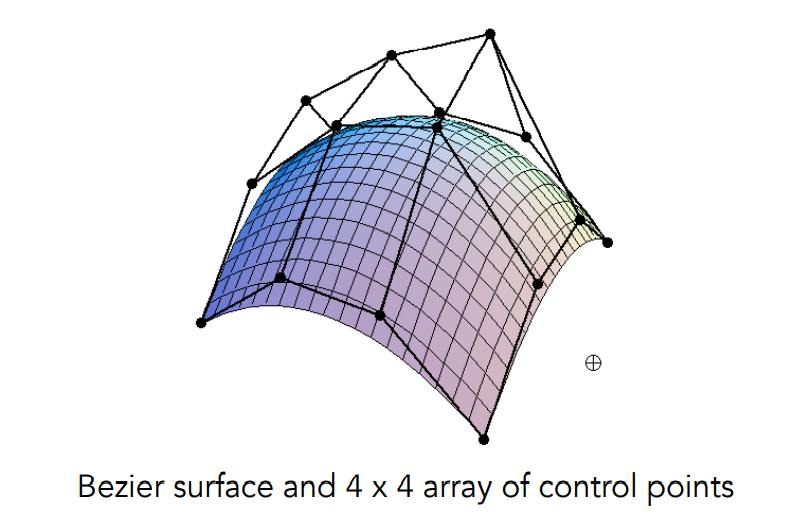
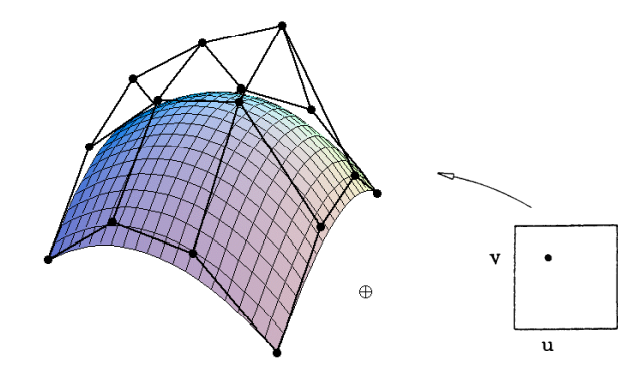
比如一个双三阶贝塞尔曲面,有16个控制点,我们先把每四个控制点所确定的贝塞尔曲线画出来:
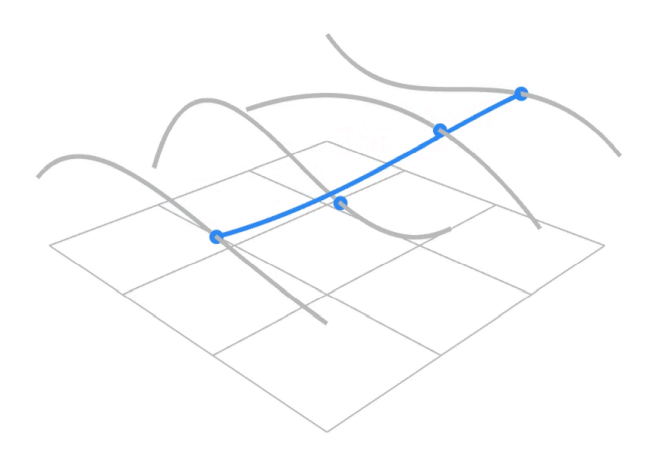
然后在这四条曲线上取四个点作为新的控制点就能确定一条新的贝塞尔曲线,四个新的控制点不停的移动就构建出了一个曲面。
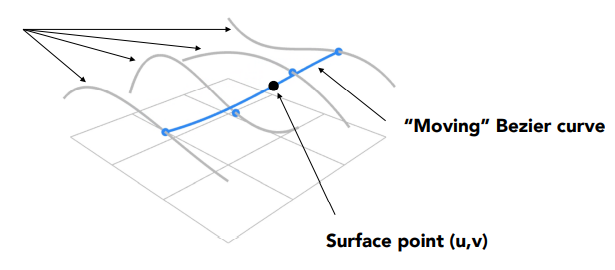
因此我们只要给定 $[0,1]^2$ 范围内的一个平面坐标 $(u,v)$,就可以对应到一个曲面上的点。
3.2 曲面操作
很多时候对于一个给定的模型,我们需要对模型上的曲面进行一些操作,如下图:

- 曲面细分:有时候模型上的曲面不够细时,我们想要使得模型更平滑更细节,就要对曲面进行细分,比如游戏中我们希望离我们近的模型细节更好,因此曲面要更多,离我们远的物体不需要太好的细节,就可以曲面少一些,减少性能消耗

- 曲面简化:刚才说的不需要太好的细节的时候就可以把曲面减少一些,也就是曲面简化
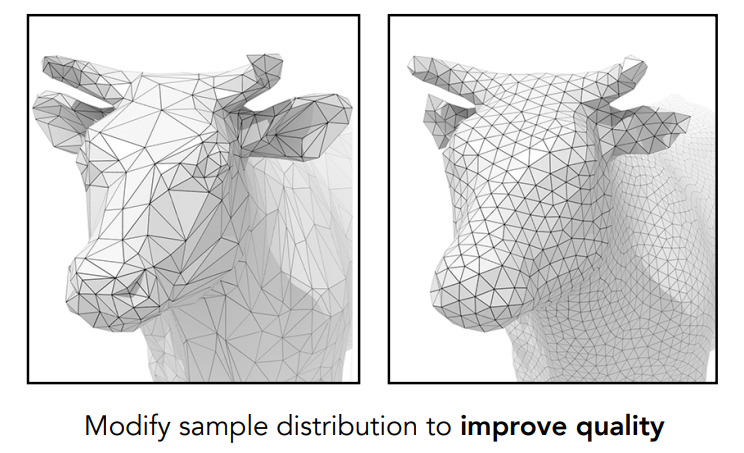
- 曲面规范化:有时候我们希望模型上的三角形的差异不要那么大,都把这些三角形规范化成近似等边的三角形,会方便我们进行一些操作,这时就需要曲面规范化
3.3 曲面细分(Mesh Subdivision)
3.3.1 Loop细分
Loop细分(不是循环细分,是发明这个算法的人家族名字叫Loop)是一种广泛使用的曲面细分算法,但它只能对三角形曲面进行细分。如下图,细分后的曲面会变得更平滑,因此细分不是简单的把三角形拆成更多的三角形,还要调整这些小三角形的位置使得整个模型发生变化,变得如我们希望的一般平滑。
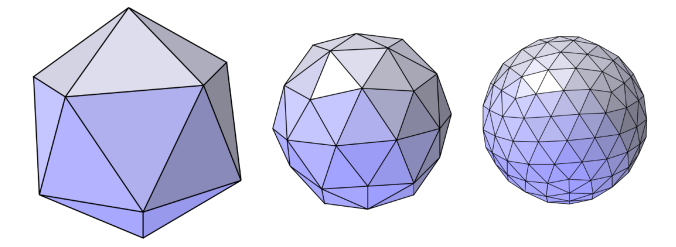
Loop细分分为两步:
1、创建更多的三角形:我们取每一个三角形三条边的中点并把它们连接起来就把一个三角形分成了4个小三角形,同时也获得了三个新的顶点
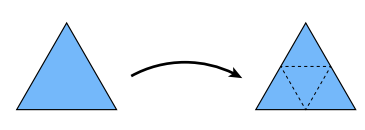
2、调整顶点位置:在经过第一步之后所有表面的顶点被分成了两类,一类是原本就有的顶点,另一类是新创造的顶点,对于这两类顶点我们用不同的方法去调整他们的位置。
对于新顶点,一定在原来的两个三角形公共边的中点处,于是我们用这两个三角形的四个顶点对新顶点位置进行更新,离新顶点近的两个原顶点权值更高:
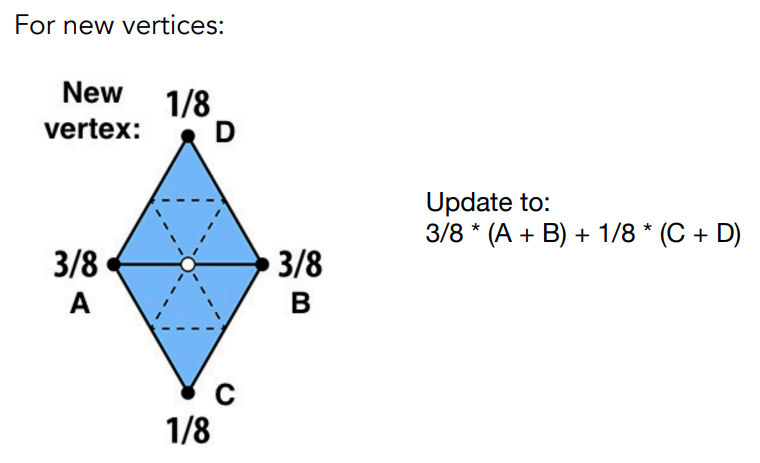
对于原来的顶点,既要参考周围其他点的位置,也要参考自己本身的位置,毕竟自己也是货真价实的一个顶点,因此对于任意一个原来的顶点,该点的度为 n (顶点的度就是和顶点相连的线段有几条,下图中顶点的度为 6 ),我们希望原顶点周围的顶点越多的时候,这个顶点对于自身位置的影响也就越不重要,因此顶点的更新规则为:
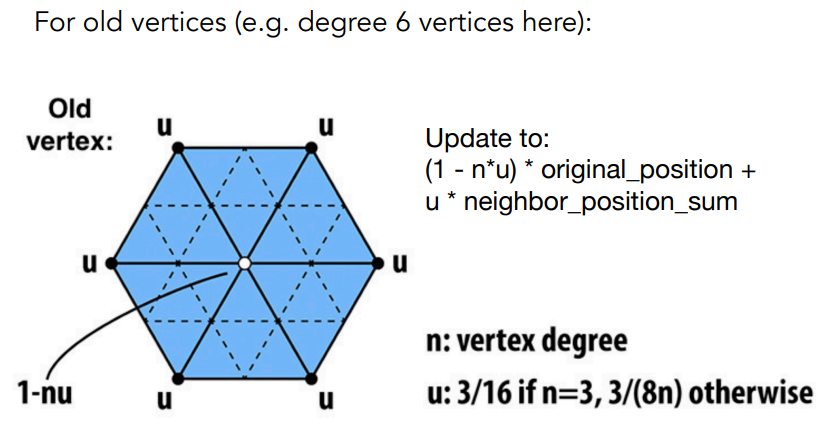
3.3.2 Catmull-Clark 细分
图灵奖得主Ed Catmull 最知名的算法之一。上面的Loop细分只能处理三角形曲面,而 Catmull-Clark 细分可以处理更一般的情况。比如既有四边形曲面又有三角形曲面的情况:
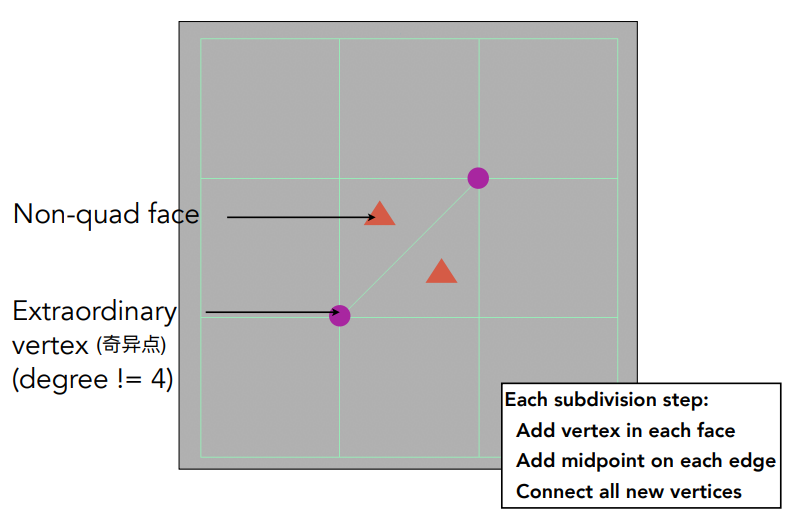
Catmull-Clark 细分把曲面分为四边形面和非四边形面,把顶点分为奇异点和非奇异点,所谓奇异点是指顶点的度不为 4 的点,上图中紫色的点就是奇异点。
Catmull-Clark 细分算法同样是先细分,再调整位置:
1、细分:我们每次细分时,找到每个曲面的边的中点,以及每个曲面的中心点,把这些点连接起来
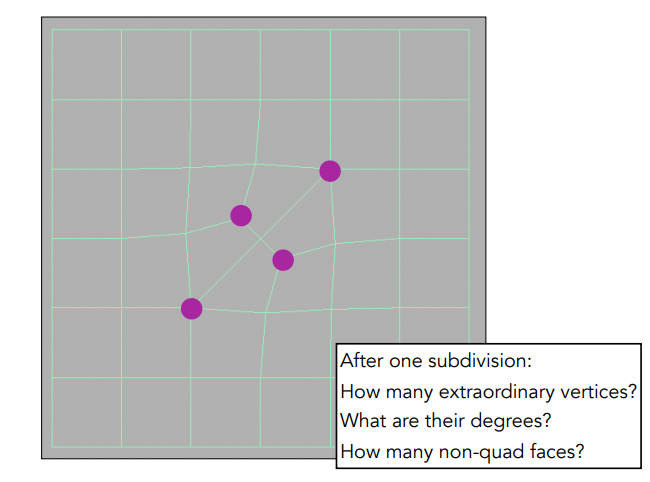
可以看到经过一次细分之后,对于四边形面,就是细分成了4个更小的四边形,而对三角形面,一个三角形被分成了 3 个小的四边形,也就是说经过一次细分后,就不再存在非四边形面了,同时我们注意到,原本有两个奇异点,经过一次细分后,新增加了两个奇异点,换句话说经过一次细分,所有的非四边形面都变成了一个奇异点,这样就不再存在非四边形面了,并且之后再进行细分也不会再增加奇异点个数了。
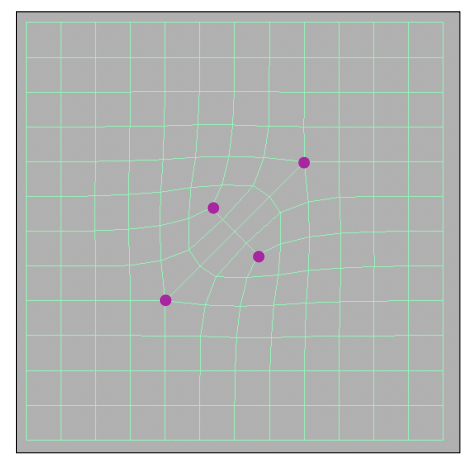
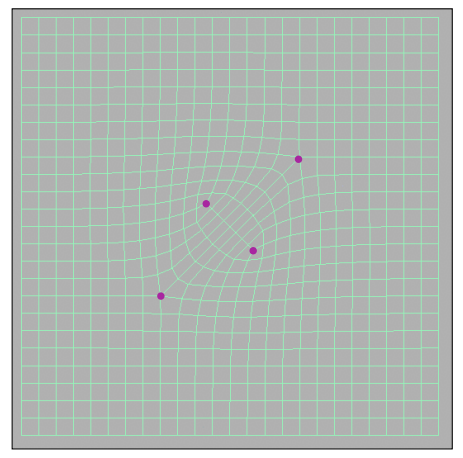
2、调整顶点位置:Catmull-Clark 细分把顶点分为三类,一类是在平面内的点(Face Point),另一类是在平面边上的点(Edge Point),最后一类是原本的顶点(Vertex point),对于这三类点的更新都是利用周围的点进行一个加权平均。

3.4 曲面简化(Mesh Simplification)
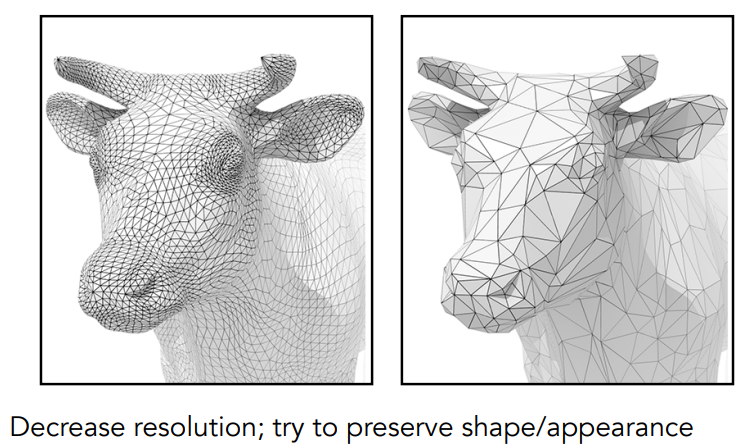
曲面简化就是减少曲面的数量,这是一个比曲面细分更复杂的问题,因为我们得保证减少了曲面数量后,模型还有原本的形状特征,而不是单纯的合并曲面。比如下面的图:

30000个三角形简化到300个三角形后丢失了很多细节但形状特征还在,如果简化到30个就完全丢失形状特征了。
曲面简化用到的方法叫做边缘坍缩(Edge Collapsing),如下图:
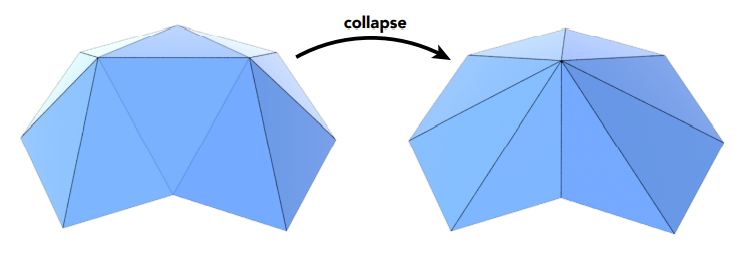
我们去掉一条边之后和这条边有关的两个曲面就消失了,其他曲面就会坍缩在一起,这样就达到了简化的效果,当然这个过程存在一个非常关键的问题,那就是我们选哪条边坍缩呢?肯定要选择坍缩后对原本模型的形状特征影响最小的边,也就是对周围平面的相对关系影响最小的边,那么如何衡量这种影响呢?
这里要用到二次误差度量(Quadric Error Metrics),我们可以计算这条边到周围平面的L2距离,也就是距离的平方和作为这条边的分数,然后我们按照分数从小到大对边进行排序,每次都选择分数最小的边进行坍缩,也就是贪心算法的思想,当然每次坍缩完之后所有边的分数要重新计算,也就是说我们每次都要能在 O(1) 时间内找到分数最小的边,同时还能对所有边的分数进行动态更新,显然优先队列或者堆非常适合来完成这个任务。
下面是曲面简化的效果:
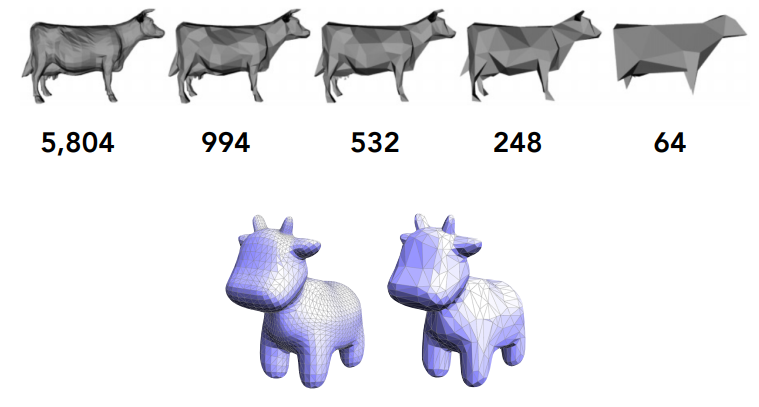
可以看到下边的小牛头部原本比较平坦,因此坍缩的边也更多,简化后形成了更大的曲面,而相对复杂的部分比如头和身体的连接处就没有进行过多的坍缩,因为这部分的边的二次度量误差一定更大,所以这里的曲面不会优先被合并。