纹理映射(Texture Mapping)
上一节介绍了着色模型和着色频率,回忆漫反射的计算,漫反射系数 $k_d$ 通常就是物体本身的颜色,但很多时候物体本身的颜色并没有那么简单,大多数情况下,物体上每一个部分的颜色都不同,物体表面具有一定的纹理,比如木质的地板,此时我们在渲染的时候也需要把这样的纹理渲染出来,这就是纹理映射。
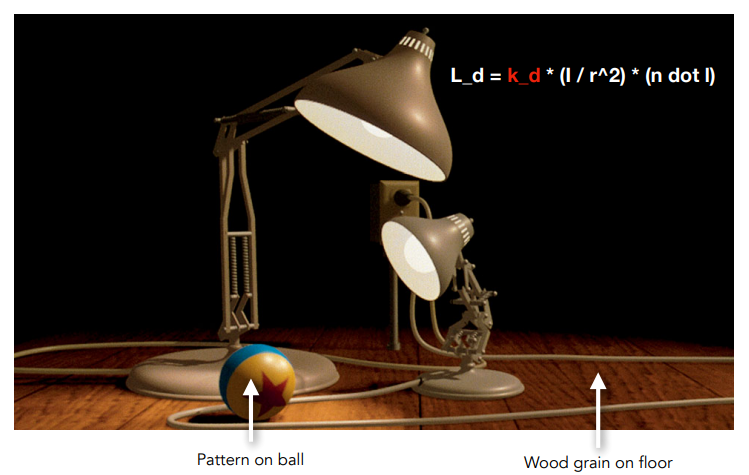
1 纹理映射
首先是一个非常简单的结论:每一个三维物体表面上的点,都可以对应一个二维平面上的点。
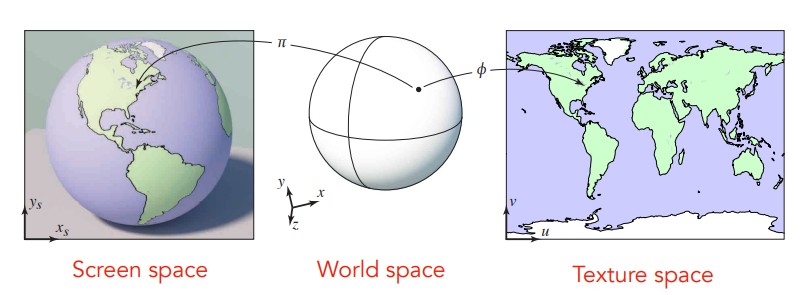
比如一个地球仪,我们把地球仪展开成一个平面,就是世界地图,相反,实际上纹理映射就是把世界地图“贴”到地球仪上。
因此对于三维物体表面的点,我们都可以把它映射到一个纹理空间中,这个纹理空间和屏幕空间一样,都是二维的,纹理空间的坐标用 $(u,v)$ 来表示,这样我们就把屏幕空间,三维空间和纹理空间联系到了一起,当然通过上图也可以看出来这三个坐标之间的关系:三维空间坐标是联系屏幕空间坐标和纹理空间坐标的桥梁,我们无法直接通过屏幕空间坐标得到对应的纹理空间坐标,因为他们之间不存在一一对应关系,屏幕上一个像素可能对应纹理空间的一个区域。这里不理解也没关系,后面我们就会遇到这种情况。
于是,最理想的情况下,三维物体上每个点都对应纹理空间的一个点,自然三维空间的三角形也就可以对应纹理图上的一个三角形,我们把这些对应的三角形的颜色都“复制”到三维图形表面的三角形上,也就相当于把一张纹理图“贴”到了模型上。
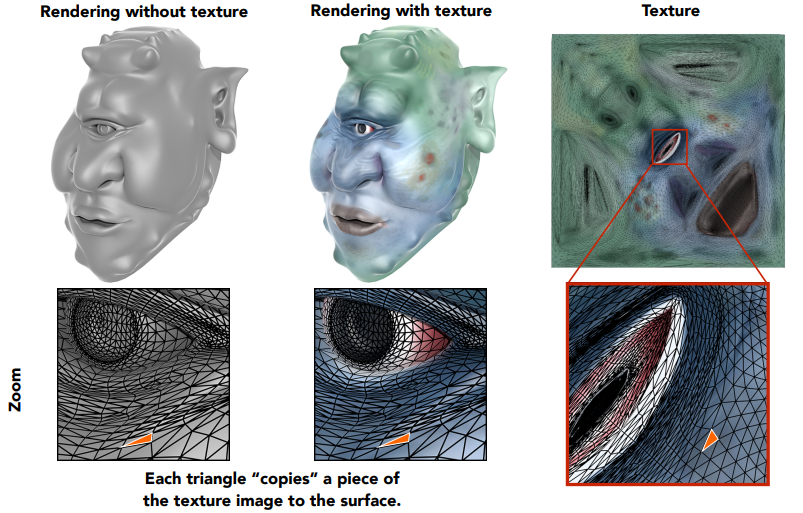
具体怎么做呢?我们对于每一个屏幕上的采样点,可以通过上一次说的三角形重心坐标插值的方法,得到这个采样点的纹理坐标$(u,v)$,然后我们根据纹理坐标直接到纹理图上查询,就可以得到纹理颜色,然后把纹理颜色作为漫反射系数 $k_d$ 去计算颜色就可以了。
2 纹理过小
上面我们了解了纹理映射的过程,其实非常简单。但实际上也没有那么简单,我们先考虑一种情况,那就是如果纹理图很小,会发生什么?
比如我们要在屏幕上画一面 4K 的墙面,但是纹理图只有不到 1K 的分辨率,这个时候屏幕上的多个像素都会映射到纹理图上的同一个像素内,我们把纹理图上的像素称为纹素 Texel,如果我们使用最近邻的方式去获得纹理颜色,那么这些像素的颜色就都会是一样的,这相当于把原本低分辨率的图暴力的放大了,于是就会出现下面左边的图这样的效果:

因此我们肯定不能用最近邻方法获取纹理颜色值,对于这种问题,自然想到插值,比如最简单的双线性插值。假如屏幕上的一个像素映射到纹理图上的坐标对应红色的点,周围黑色的点是纹素中心:
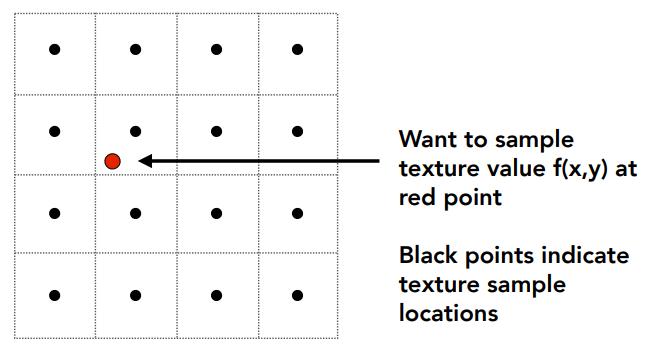
双线性插值选取该点周围最近的四个纹素:
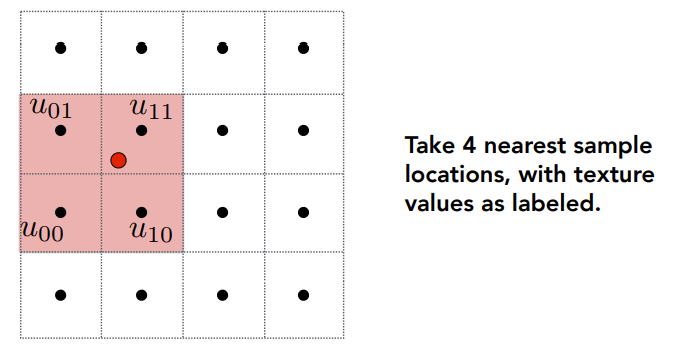
计算在水平和垂直两个方向上的相对偏移系数,偏移系数都在0~1之间,我们假设两个纹素之间的距离是 1:
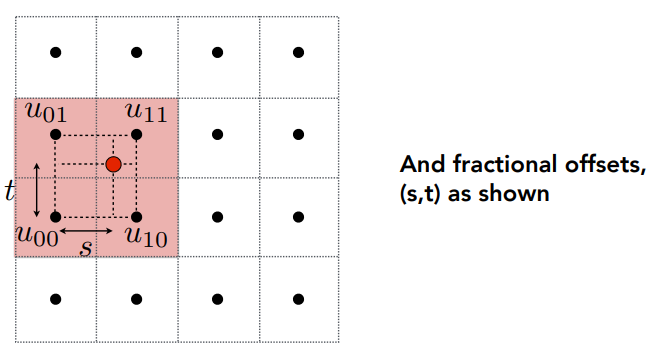
然后先做一次水平插值:

再做一次竖直插值:
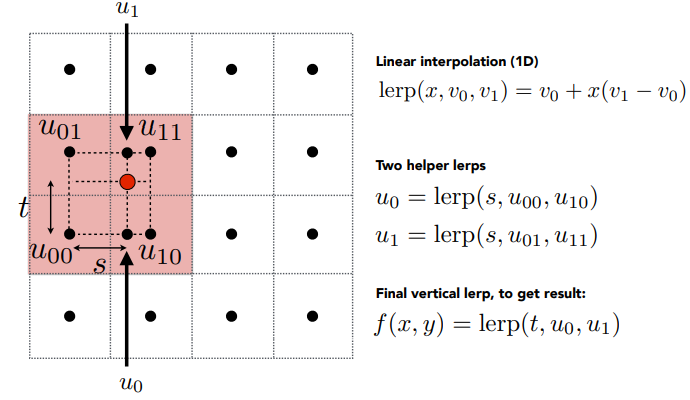
一共做了两种线性插值,所以叫做双线性插值。然后将插值的颜色作为该点的纹理颜色返回,这样就可以使得屏幕上的像素过度的更柔和一些,下面中间的图就是双线性插值的结果。

当然还可以使用更复杂的双cubic插值,会选取周围16个点做两次cubic插值,效果会更好,当然运算开销也更大,最右边的图把眼角处细微的锯齿都去掉了。
3 纹理过大
讨论完了纹理图过小产生的问题,接下来考虑如果纹理图过大又会发生什么呢?
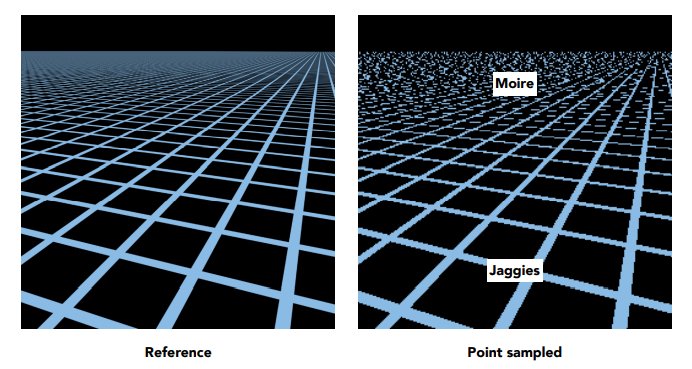
可以看到,当纹理图的分辨率过大时,产生了锯齿和摩尔纹,也就是发生了走样。为什么会走样呢,回顾之前说的走样产生的原因,是因为采样频率跟不上信号变化的频率,当纹理图过大时,屏幕上一个像素对应到纹理图上可能是一片区域:
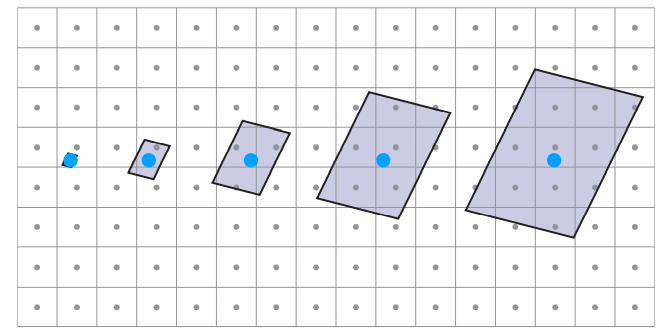
这一片区域中每一个纹素颜色都可能不同,这相当于在一个像素内,信号(也就是颜色)发生了剧烈的变化,这也就是采样频率低于了信号的变化频率,也就发生了走样。此时如果我们用区域内的一个纹素值代表整个区域的颜色显然是不合理的。因此我们要进行纹理映射的反走样。
反走样之前也讲过,最简单的反走样就是增大采样频率,比如类似于MSAA的超采样,我们可以把一个像素分成好多个像素去映射到纹理图上,然后获取这些子像素的纹理颜色,最后加权整合成像素颜色。效果如下:

可以看到效果还不错,但为了得到这样的效果进行了512倍超采样,消耗太大了,如果纹理图更大呢?我们没有办法无穷尽的进行超采样,因此最好是换一种方法。
反走样是因为采样产生的,那我们可以不直接不采样,如果我们能直接获取到纹理图上某个区域的平均值,就不需要进行采样了。我们直接把像素对应的区域的平均值拿到就可以了。如何做到呢?
3.1 Mipmap
Mipmap是一种非常快速的,空间开销很低的,近似的,区域查询方法,但只能查询方形区域。
Mipmap的思想非常简单,我们把一张图片每四个像素计算一个平均值,这样全图计算一次之后,图片尺寸就缩小了一半,这个图片中每个像素的值就是原图一个正方形区域四个像素的平均值,之后继续这样缩小下去,就得到了不同级别的原图的多个像素的平均值构成的图:

由于每次图片尺寸缩小一半,那么像素数就只有原来的四分之一,所有级别的图加起来所花费的额外存储空间也不过原图大小的三分之一(简单的等比数列求和)。
接下来就是如何去查询信息了。我们把屏幕空间中的一个点和它水平和垂直方向相邻的点都映射到纹理空间中,就得到了纹理空间中的三个点(也可以是四个,把对角线上相邻的点也映射过去就是四个点,具体看后续是否用得到);
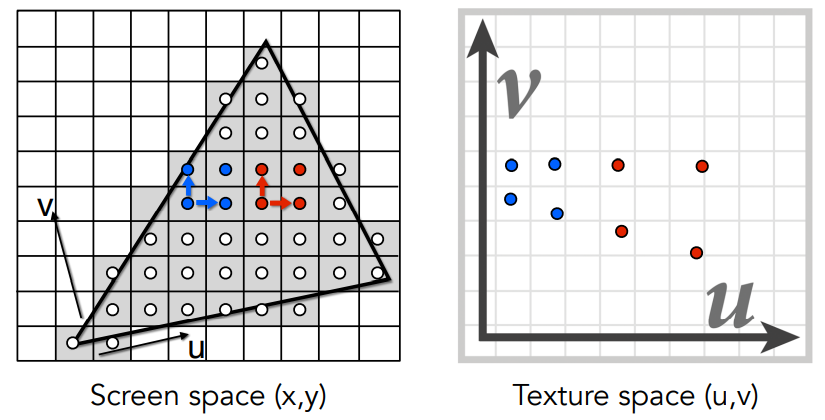
然后我们计算映射后该点和其他两个点的距离,把这个距离取最大值作为以该点为中心的正方形区域的边长,这样就近似得到了屏幕上一个像素在纹理空间中对应的一片正方形区域。然后查询这片区域的平均值即可,查询的级别 $D=log_2L$,D取整数。
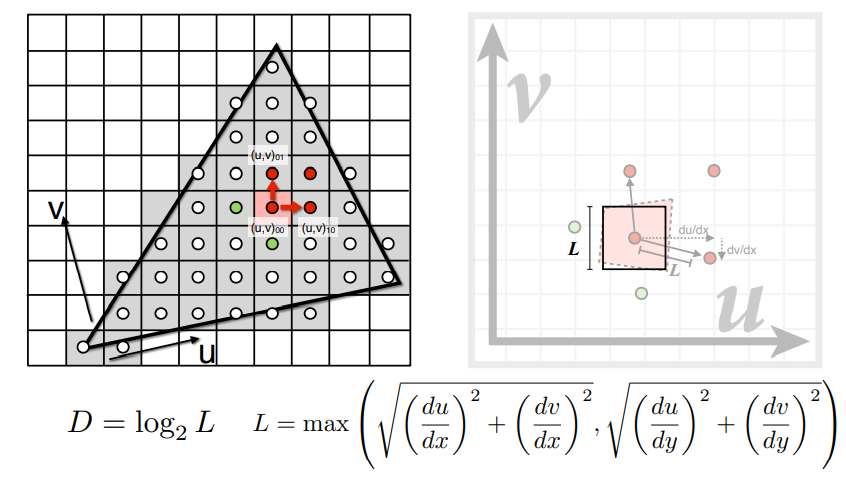
下面是按照上面的算法,一个场景中每个像素要查询的Mipmap的级别可视化的效果:

可以发现Mipmap级别 D 取整数会造成屏幕上相邻像素查询的级别可能差别很大,最后渲染出来的图可能会有严重的割裂现象,因此我们希望查询的级别也能平滑过渡,我们希望可以查询 1.8 级的Mipmap,又是平滑过渡,因此又是插值。
我们可以去查询两个级别的Mipmap,在Mipmap内部使用双线性插值得到两个级别的平均值,然后再将这两个级别进行线性插值得到最终结果,也就是进行了三线性插值:
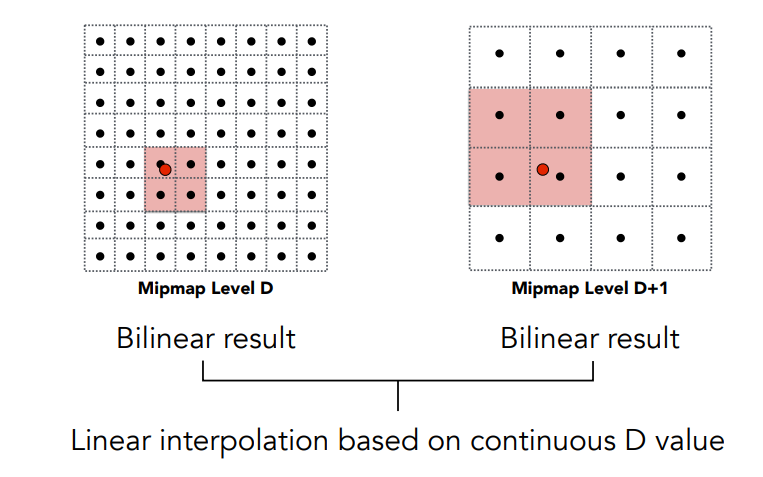
使用三线性插值后,Mipmap级别可视化的效果如下:

过度非常平滑,达到了我们想要的效果。
最后看一下使用Mipmap渲染出来的图片是什么样子:
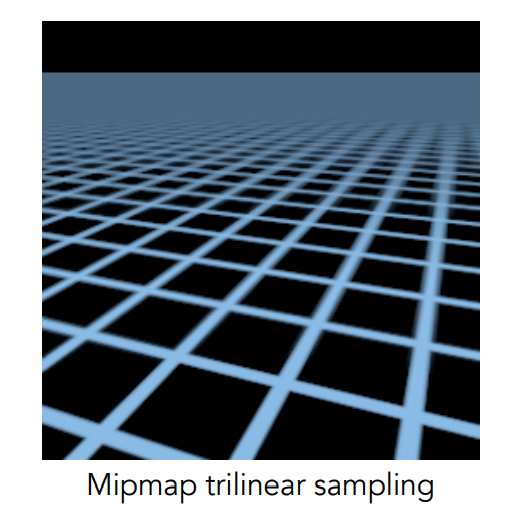
3.2 各向异性过滤
可以看到Mipmap渲染的图形中,近处的锯齿消失了,但远处产生了过度模糊,这是因为Mipmap只能近似方形区域,而这张图上近处的像素映射到纹理空间中对应的区域非常小,因此无论这个区域是什么形状,近似成正方形都不会有太大的问题,但是远处的一个像素对应到纹理图上可能是很大一片区域,此时这个区域的形状就会对结果产生影响了,如下图所示:
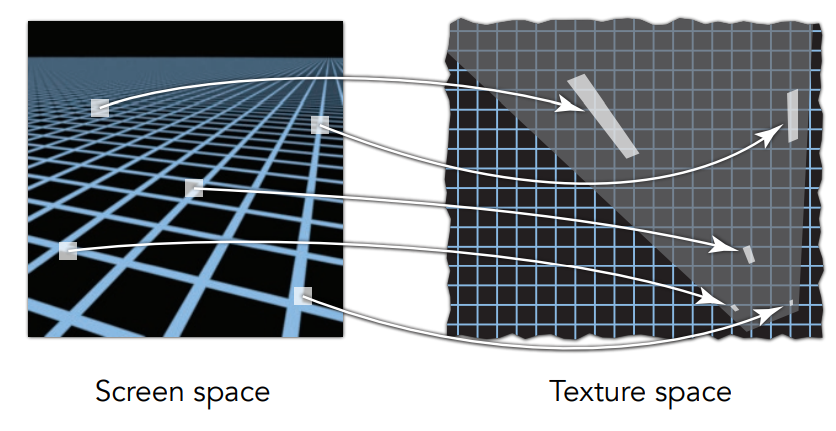
区域很大时,如果形状不是正方形而是一个矩形,那我们按照Mipmap的方法实际近似的区域其实是这个矩形的Bounding box,这与原来的矩形区域差别很大,所以Mipmap不能完美的解决走样问题。
因此现在游戏中使用的更多的是各向异性过滤技术。

各向异性过滤是Mipmap的改进,它不仅每次等比例的缩小原图,还会长宽不等比例的去计算Mipmap,这样缩小的图上一个像素对应的就是原图上一个矩形区域内像素的平均值了,然后我们就可以支持矩形的查询了。但斜向的矩形查询仍然存在问题。
除此之外的反走样方法还有EWA过滤,如下图,是用多个圆形或者椭圆形去近似填充任意几何图形,但是需要多次查询,不过可以查询任意形状的区域。
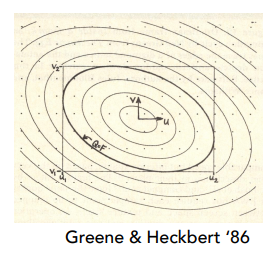
4 纹理的应用
前面就是纹理映射的全部基本的内容,现在我们要把纹理推广开来。
纹理不是一张简单的图片。在现代GPU中,纹理就可以理解为一块可以支持快速范围查询的内存。而上面我们所说的纹理图,只不过是纹理的一种用法而已,纹理图其实就是把颜色存入这块内存,供我们随时查询,取用。当然我们也可以存别的东西,所以纹理可以有各种各样的用途。
4.1 环境贴图
一些光面的物体还会反射环境中的景象,这怎么做到呢?也是利用纹理实现的。

我们可以提前把整个环境的图存下来,渲染物体颜色的时候把环境作为一个纹理应用到物体上就可以了。
我们假设用一个球来存储环境贴图,如下图:
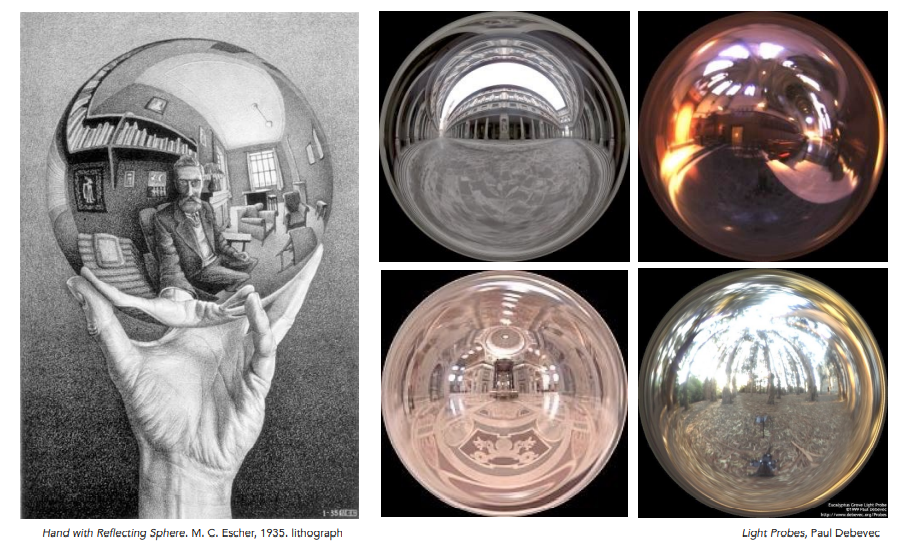
那把这球的表面展开成平面,就得到了整个场景的环境贴图:

但我们会发现这张帖图有一点问题,就是边缘会产生扭曲,因为球顶部的面积更小,所以造成了扭曲。因此人们想到用立方体存储不是更好吗?
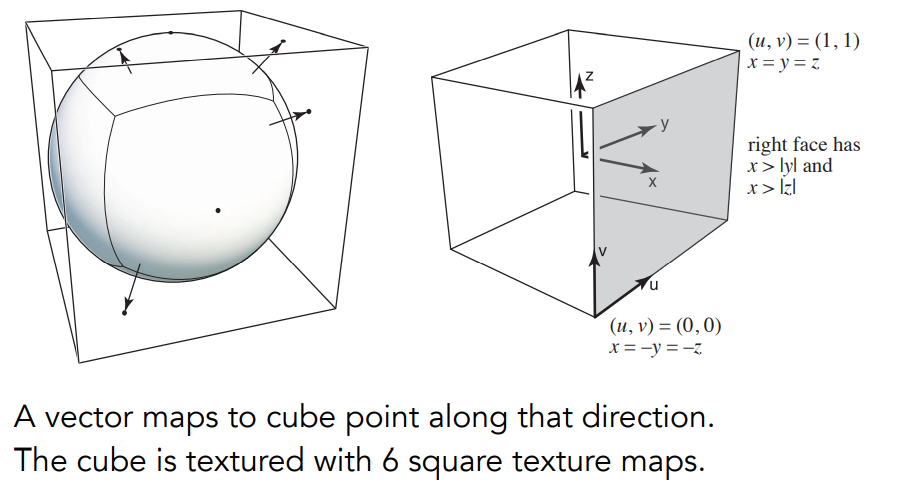
把球的每一个面“贴到”立方体的每一个面上,就可以用立方体存储整个环境,大概的效果:

4.2 凹凸贴图
有时候我们希望渲染出物体表面凹凸不平的样子:

这时我们可以用凹凸贴图来解决。想要造成凹凸的效果,其实就是在计算光照时,将顶点或者平面的法向量向上或者向下移动一定的距离,这样计算出的光照就有明显的明暗变化,在我们看起来也就产生了凹凸的效果,因此我们可以用纹理存储每一个顶点法向量的扰动量,然后再计算光照时取到这个扰动量施加到原本的法向量上去计算光照,就得到了凹凸的效果。具体怎么计算扰动后的法向量呢?
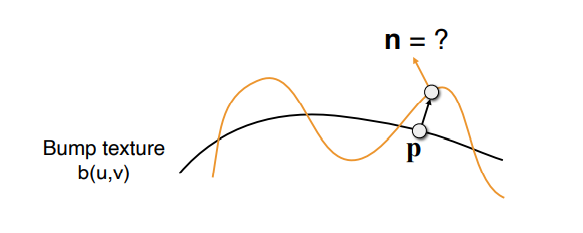
我们先考虑简单的二维情况:
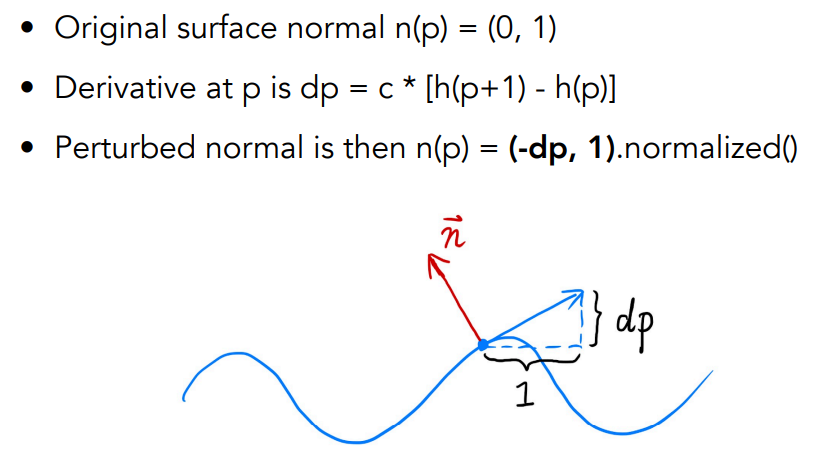
假设原本平面的法向量是$(0,1)$,我们可以计算出扰动后的点在曲线上的导数(切线),然后可以直接得到和切线垂直的方向,这就是扰动后的点的法线方向,最后别忘了归一化。
推广到三维空间中,我们每次计算都把当前点的法向量转换到以这个点为基准的局部坐标系下,这样当前点的法向量就是$(0,0,1)$,然后同样计算在两个方向上的导数:
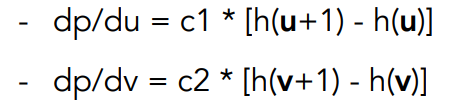
于是扰动后的法线方向就是:

最后再从局部坐标系转换回原本的坐标系即可。
4.3 位移贴图
使用凹凸贴图可以渲染出凹凸的效果,但是其实只是在计算光照时改变了顶点的法向量,而顶点本身没有发生任何变化,所以我们看到的凹凸效果只是一个假象,很容易看出破绽:
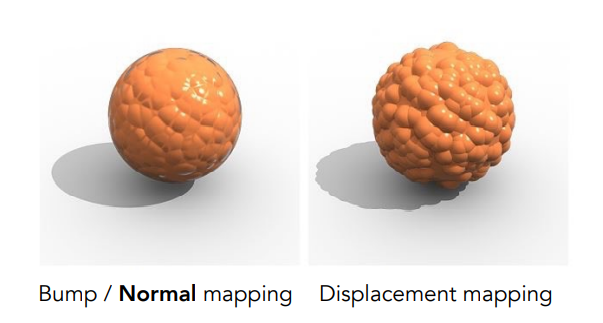
凹凸贴图渲染出来的模型边缘还是平滑的。而位移贴图可以渲染出真正凹凸不平的效果。
位移贴图存储的是每个顶点的位移,也就是它真正改变了点在空间中的位置,这样自然模型的形状也就发生了变化,渲染的效果也会更真实。
那为什么不直接做一个这样的模型呢?显然这么复杂的模型如果直接在建模的时候就做好,要花费大量的精力,所以位移贴图要方便许多。
4.4 三维噪声和固体纹理
有一些纹理比如瓷器上的纹路,是完全不规则并且独一无二的,这时候如果我们给每一个花瓶一个不同的贴图显然是不现实的,因此我们可以给定一个三维程序噪声函数,在计算颜色的时候利用这个噪声函数生成随机的纹路。
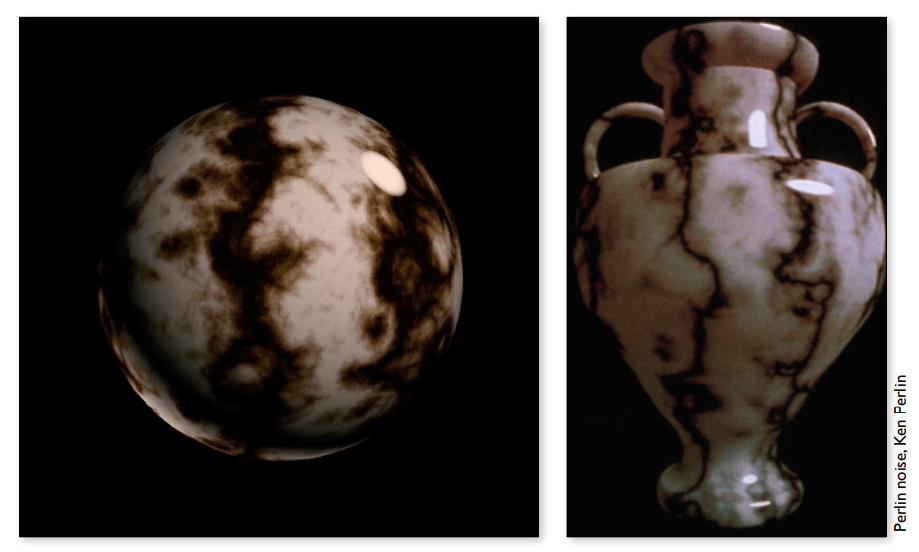
有时候我们的模型内部也需要有一定的纹理,比如大理石切开之后的纹理,那我们可以把整个大理石的表面和内部的全部纹理信息都存下来,存储成一个三维的纹理,这样对应空间中每一个点都有不同的纹理。
4.5 环境光遮蔽
我们在计算shading的时候并不会考虑模型本身对模型光照的影响,比如下面这张图:
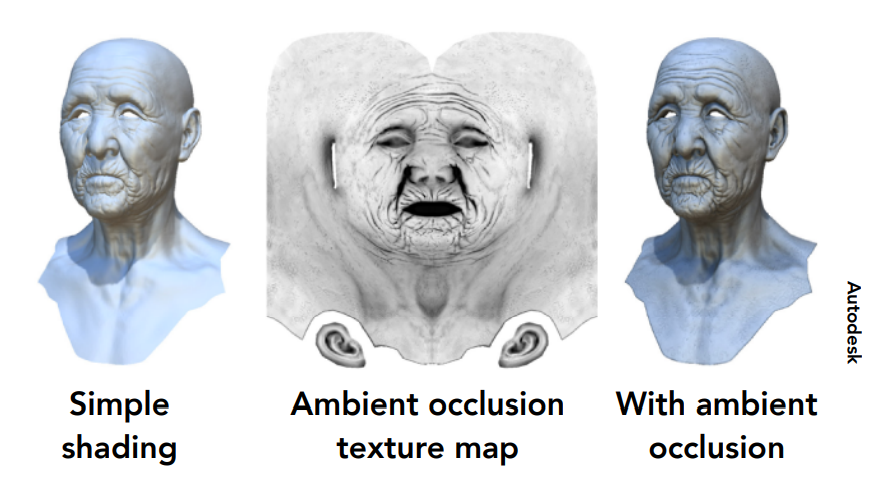
模型本身可能会对光照有一定的遮挡,导致不同部分产生一些阴影,左边的图就是正常着色的结果,可以看到眼眉处没有阴影,显得不是很真实,因此我们可以预先计算模型本身对光照的影响,生成一张阴影纹理图,在之后着色的时候加到着色结果上,就有了更真实的渲染结果,这也是环境光遮蔽的原理。