着色(Shading)
前几节我们介绍了三维中的各种变换,三维到二维的映射,以及如何在屏幕空间中渲染三维空间中我们所看到的物体,也就是光栅化。光栅化的过程实际上就是判断像素是否在三角形内,如果在就填上对应的颜色的过程。那么从这一节开始,我们将讨论“填上对应的颜色”这里的颜色从何而来。
1 什么是着色?
现实生活中我们之所以能看见东西,是因为光线和物体本身发生了某些”作用“,而我们看到的世界实际上是发生这个作用之后的世界,那对于计算机而言,我们给定了相机、模型以及场景,利用前几节的内容我们实际上就能显示出相机看到了什么,但显示出的内容和实际我们应该看到的内容有很大的区别,原因在于我们没有考虑光线和物体所发生的”作用“,当光线照到物体上时,我们所看到的物体的颜色,一定和实际物体的颜色是不同的,比如下面这张图,相信这也很好理解:

立方体本身的颜色一定是一样的,但我们看到的每一个面颜色都不同,这就是光线的作用,因此我们要想画出来实际看到的场景,就要知道我们看到的模型的每一个部分是什么颜色的,而不是模型本身是什么颜色的,这也就是着色所做的工作。当然上面的图是很简单的情况,实际应用中我们渲染的场景可能非常复杂:

可以看到这个场景具有复杂的光照条件,包含了各种不同材质的物体,还包括透明的液体,还有右边杯子上倒映出的周围环境的镜像,这些都是我们眼睛看到的,而不是物体本身具有的,着色就是要根据物体本身具有的属性,以及环境的光照计算出物体上每一个点在我们的视角下,应该被看到的颜色。
2 Blinn-Phong着色模型
通常来说光线与物体之间的”作用“可以描述为以下三种,如下图所示:

一种是我们看到的非常亮的反光,叫做高光(Specular highlights);另一种是物体颜色上细微的渐变,也就是漫反射(Diffuse reflection);最后是没有被光线直接照射到但也可以被看到的部分,因为有间接的光线照射到了这部分,也就是环境光或间接光照(Ambient lighting)。
在展开介绍之前要先明确,我们计算着色永远是在进行局部的计算,因为物体上的每一部分都和光线有不同的角度,所以也就发生不同的反应,我们计算的这个局部的点称为着色点,这也是一个抽象的概念,着色点可以是一个点也可以是一个平面,平面可以理解为这个点抽象而成的无限小的平面,我们计算各种光照时,都是光线在与这个平面发生作用。
计算着色其实就是计算上面三种光照,对于这三种光照的计算,输入都是一样的:
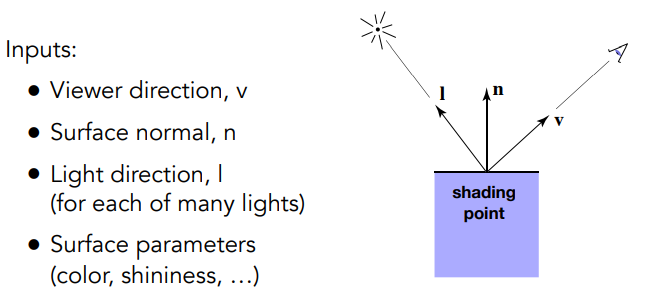
输入包含我们观察的方向向量$\vec v$,着色点的法向量$\vec n$,光线的入射方向$\vec l$以及着色点表面的属性,也就是颜色等信息。需要说明的是这三个表示方向的向量只表示方向,因此都是单位向量。
2.1 漫反射
漫反射非常简单,就是光线射到物体表面时会朝各个方向均匀的发散:
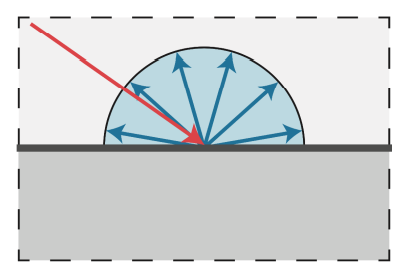
也就是说,物体表面的颜色从各个方向看都是相同的,决定物体颜色深浅的,只有物体接收到光线之后,吸收了多少光,又反射出去了多少光,反射出去的这部分,也就是我们看到的颜色。
于是首先要考虑物体能接收到多少光。如下图所示:
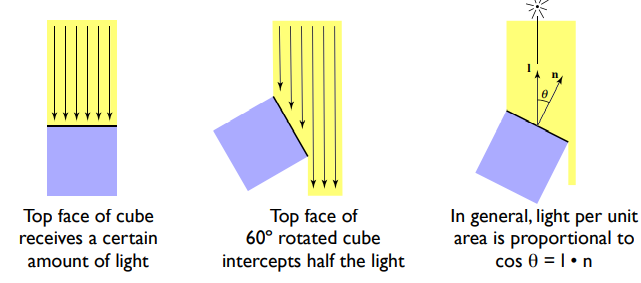
物体表面如果和光线入射方向垂直,那就接收到了几乎全部的光,而如果物体旋转一定的角度,就有一部分光到达不了物体表面,也就无法被接收,而到达物体表面的光,也与物体表面有一定的角度,能量也是无法被完全接收的,那如何描述这个关系呢,Lambert’s余弦定理给出了答案:物体表面单位面积的光照与平面法线和光线夹角的余弦成正比。这里的光线方向是从物体表面指向光源的方向,是光线入射方向的反方向。
那么光的强度又该如何描述呢,光可以理解为一种能量,所以在传播的过程中能量一定是有所损失的,所以光的强度与传播距离是成反比的,如果光源处强度为$I$,那么距离光源 $r$ 处的强度为$I/r^2$.
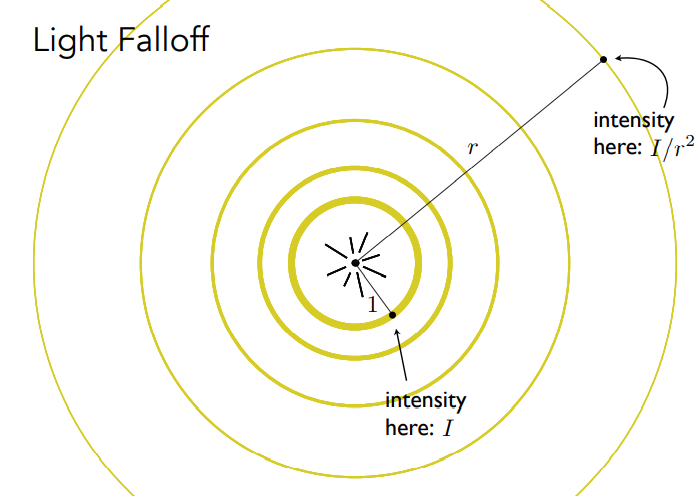
于是我们就可以得出漫反射的计算公式: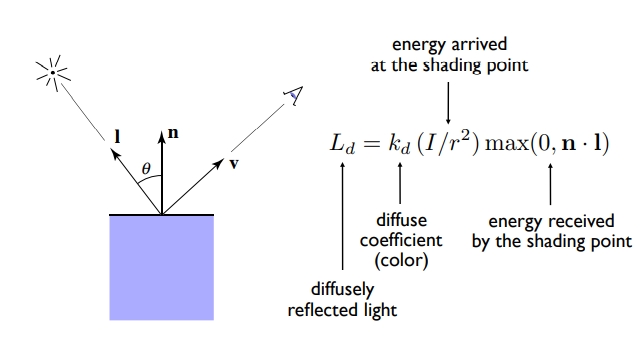
$k_d$ 是漫反射系数,也就是着色点的颜色;平面法线和光线夹角的余弦也就是着色点的法向量$\vec n$和光线的入射方向$\vec l$的点乘,因而二者都是单位向量所以点乘就是余弦,$max(0, \vec n·\vec l)$的含义是有时夹角余弦为负,那我们认为这是无意义的,因为这相当于光线从平面下方射入,实际上就是看不到任何颜色,所以如果夹角余弦为负我们就取0.
可以看出漫反射计算中不包含视线方向 $\vec v$ ,正好对应开头说的,漫反射与观察方向无关,漫反射的颜色从任何方向看都是一样的。
下面的图展示了$k_d$ 逐渐增大对应的漫反射表现,也就是颜色逐渐变亮。

2.2 高光
当我们的视线方向和光线的镜面反射方向比较接近时,就产生了高光:
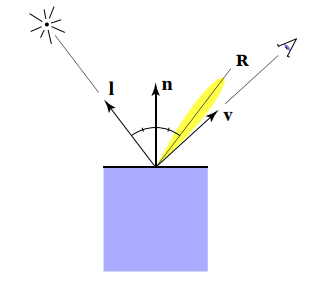
所以我们只要计算镜面反射方向 $\vec R$ 和观察方向 $\vec v$ 的夹角余弦就可以,高光和这个夹角余弦成正比。
在布林冯模型中没有直接计算镜面反射方向 $\vec R$ 和观察方向 $\vec v$ 的夹角余弦,而是进行了优化:
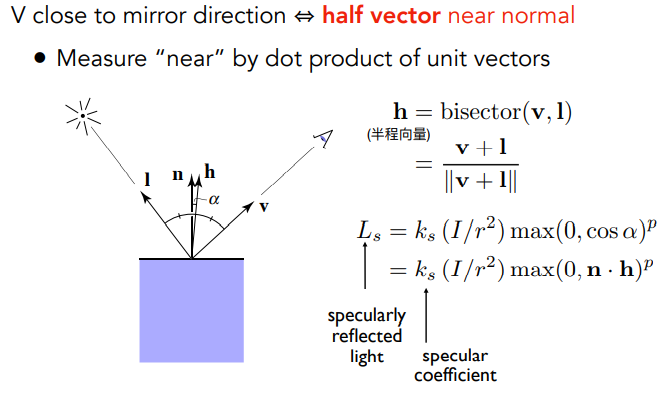
镜面反射方向 $\vec R$ 和观察方向 $\vec v$ 接近可以转化为着色点法向量和半程向量接近。所谓半程向量是指光线入射方向和观察方向的角平分线方向,这个向量非常容易计算,根据向量的平行四边形法则,半程向量就是光线入射方向向量和观察方向向量的和。
于是我们就得到了上面的高光计算公式,和漫反射非常类似,$k_s$ 是高光系数,也就是高光的颜色,一般就是白色,与漫反射唯一不同的是,高光计算公式中夹角余弦部分多了一个指数 $p$,这是因为余弦函数本身的容忍度太高,如下图:
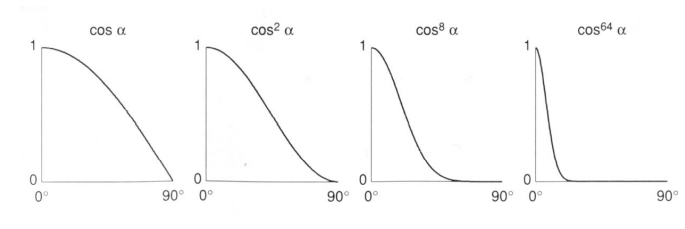
如果直接使用余弦函数,那么镜面反射方向和观察方向夹角45°甚至更大时,我们还会取到一个比较大的值,此时意味着我们还可以看到比较明显的高光,但实际上我们只有在镜面反射方向和观察方向夹角非常小时才能看到高光。可以看到随着余弦函数幂次的增大,我们能看到高光的夹角阈值在变小,当我们使用余弦函数的64次方时,只有在镜面反射方向和观察方向夹角大约20°范围内才能看到高光,当然这还是太大了,所以在布林冯模型中 $p$ 的取值一般在100~200左右。
下面的图每一行展示的是随着 $p$ 取值增大所看到的高光的效果,每一列代表的是高光系数 $k_s$ 增大带来的变化,就是高光部分的颜色越来越亮。

2.3 间接光照
间接光照最为简单,间接光照就是从四面八方射向物体表面的各种光对物体颜色产生的影响的总和,与光线的入射方向、物体表面的法线方向和我们的观察方向都没有关系,所以间接光照就是一个常数。

2.4 布林冯模型
将上面的三个光照项加起来就得到了物体表面受光照影响的总和,这就是布林冯着色模型。

可以看到最左边间接光照就是一个固定的颜色(常数),漫反射表现的是物体表面颜色的变化,这个变化是由物体表面和光线方向不同引起的,高光是一些白色的亮光,只有物体上使得光线镜面反射方向和观察方向夹角比较小的部分才会显示出高光。这些项全部叠加起来也就是最终我们看到的物体的颜色了。
3 着色频率
到此为止我们了解了对一个着色点应该如何着色,那么对于一个物体,我们该以什么样的方式去对整个物体表面进行着色呢?有以下三种方式:

- 最左边是对物体上的每一个片面(也就是组成物体的基本几何图形,可以是三角形,可以是矩形),进行一次着色,此时这一个片面就是一个着色点,所以这个片面内计算出的颜色是一致的,可以看出着色效果并不好
- 中间是对物体上的每一个片面的每一个顶点进行一次着色,此时每个片面的顶点是一个着色点,片面的颜色取决于计算出的这些顶点的颜色,可以用插值的方法得到每个片面的颜色
- 右边是对物体上每一个点进行一次着色,此时每一个点都是一个着色点,因此效果也最细腻
上面三种着色方式代表着三种不同的着色频率,其中也包含很多具体的问题,接下来具体介绍这三种着色方式。
3.1 Flat shading
Flat shading对物体每一个片面三角形进行着色,是最简单的着色方式,但是对于平滑表面着色效果不好。

3.2 Gouraud shading
Gouraud shading对物体上的每一个三角形的每一个顶点进行一次着色,计算出每个顶点的颜色后,对三个顶点颜色进行插值就可以得到三角形上每一个点的颜色。

具体如何插值后面会专门介绍,除此之外还存在一个问题,就是一个顶点怎么计算它的法向量?
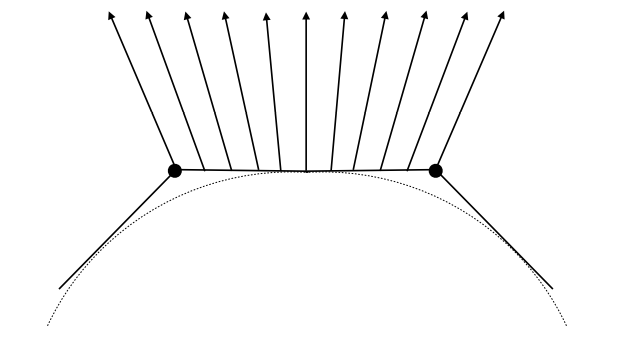
我们首先考虑一个简单的二维情况,如果这个顶点是一个圆上的点,那么这个点的法线方向就是圆心和这个点连线的方向,如果这个点是圆某个内接多边形的顶点(圆上任何一个点都可以是内接多边形的顶点),那么法线方向就是与这个顶点相邻的两条边的法线的角平分线方向,也就是两条边的法向量的和。
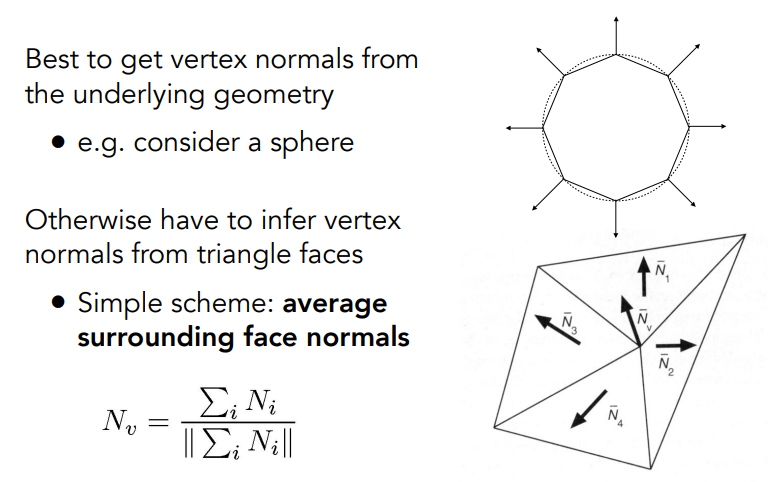
推广到三维中,物体上一个点的法线方向就是与它相邻的所有平面法向量的加权和。加权是因为实际应用中三维物体不可能都是一个均匀球体,会是各种形状,所以每个相邻的平面也不一样大,自然对这个顶点法线方向的贡献也不同。
知道了如何计算点的法向量,也就知道如何进行Gouraud shading了。关于三角形颜色的插值,后面会统一介绍。
3.3 Phong shading
Phong shading对模型上每一个点进行着色计算,因此每一个点都是一个单独的着色点。那么又出现一个问题,我们如何计算物体上每一个点的法向量呢?

由于这些点大部分都不是片面三角形的顶点,所以上面的法线计算方法并不适用。但我们可以先计算出片面三角形顶点的法向量,再利用插值的方法得到三角形内每一个点的法向量,当然别忘了计算完成后对法向量进行归一化,法向量只指示方向,一定是单位向量。
和上面的颜色插值一样,这里又要用到三角形的插值,只不过这次插值的内容是法向量。接下来我们专门介绍三角形的插值方法——利用重心坐标。
4 重心坐标(Barycentric Coordinates)
三角形插值是图形学中经常使用的操作,因为很多时候我们只知道三角形三个顶点对应的某些属性值,那么想要使得三角形内部每一个点的属性值平滑的变化,就需要利用已有值进行插值。于是引入三角形重心坐标的概念。
重心坐标实际上是一个坐标表示方法,对于空间中的三角形ABC,任意一个在三角形ABC平面上的点$(x,y)$,都可以表示为三角形三个顶点坐标的线性组合$\alpha A+\beta B+ \gamma C$,其中三个系数就是这个点在这个三角形下的重心坐标,重心坐标需要满足约束$\alpha + \beta + \gamma=1$,如果不满足这个约束,表示出来的点就不在三角形ABC这个平面上;并且如果这个点在三角形内部,重心坐标三个数都非负。
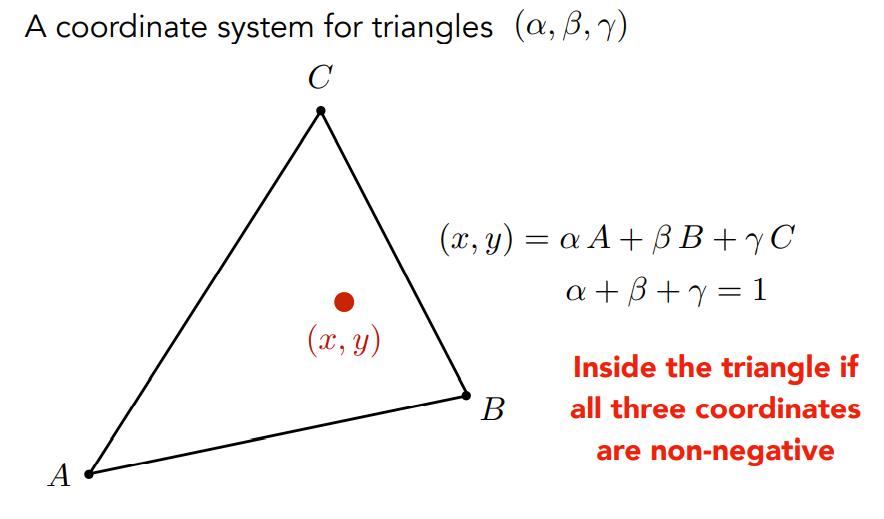
有了重心坐标的定义,那对于三角形内部的任意一个点,怎么去得到它的重心坐标呢?
对于三角形内部任意一个点,将它和三个顶点相连,会形成三个子三角形,重心坐标可以根据三个子三角形面积求出:
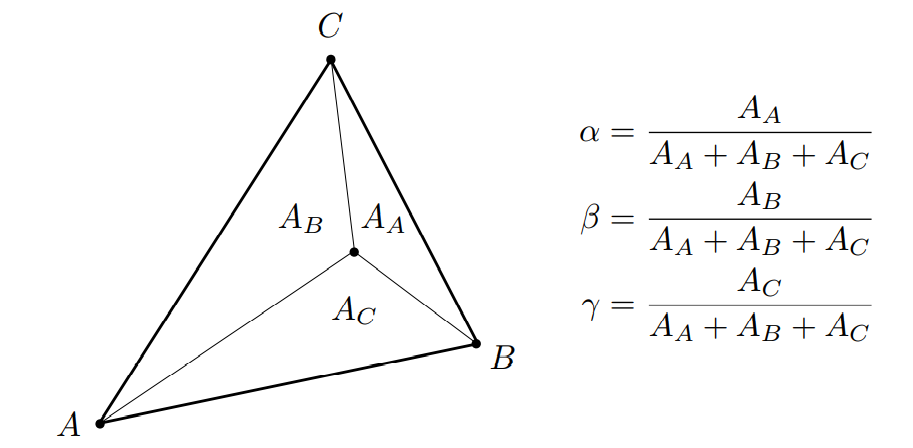
每个顶点对应的系数等于该顶点对面的子三角形面积除以三角形的总面积,比如点 A 的系数 $\alpha$ 等于点 A 对面的子三角形,也就是和点 A 不相邻的子三角形$A_A$的面积除以三角形ABC的总面积。
显然三角形重心的重心坐标就是:
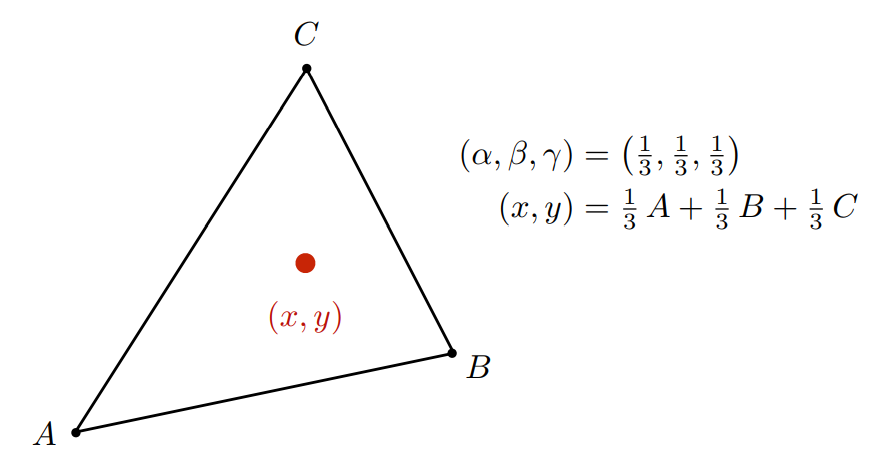
给定三角形的三个顶点和三角形内任意一个点坐标,我们可以根据下面的式子求出该点的重心坐标:
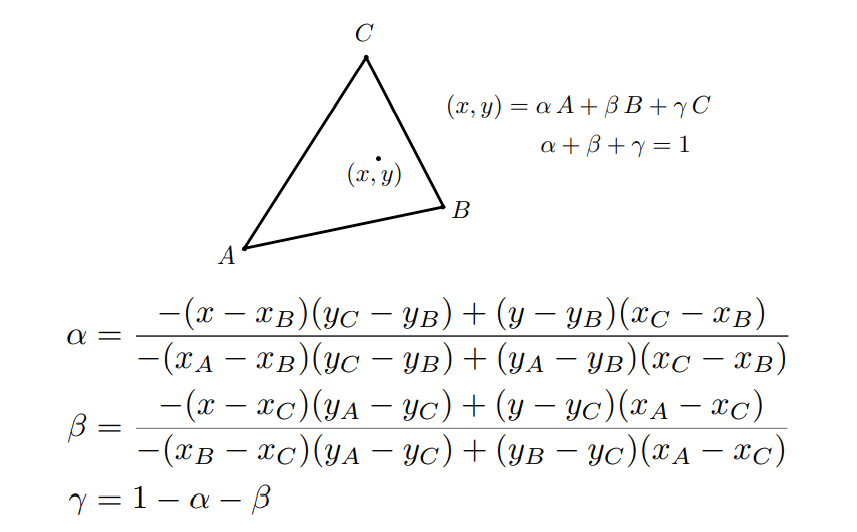
得到重心坐标后,再进行三角形内部的线性插值就非常容易了,因为线性插值就是把三角形内任意一个点的某项属性(属性可以是坐标、颜色、深度、法向量等等)表示为三角形三个顶点属性的线性组合,至于怎么组合,重心坐标就是“坐标”这个属性的组合系数,自然也可以用在其他任何属性上。
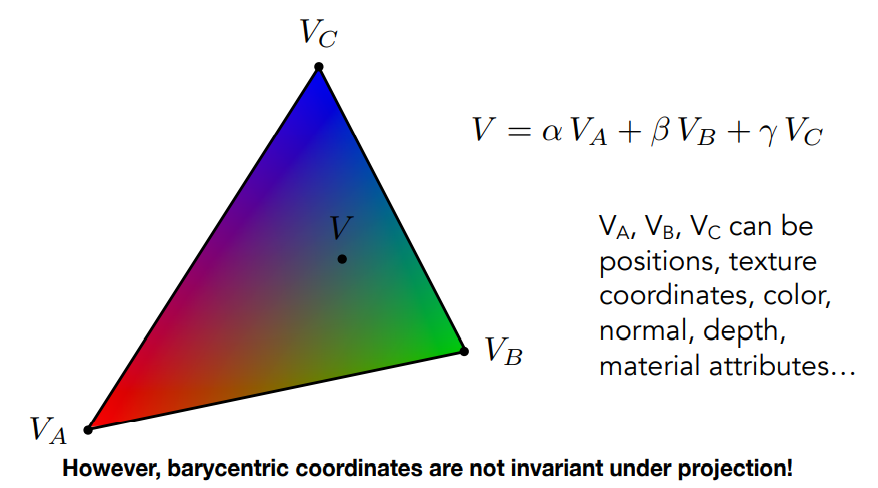
需要注意的是,重心坐标不具有投影不变性,因为空间中的三角形投影到平面上,形状可能会变化,那么三角形内每个点的重心坐标自然会发生变化,因此计算和空间有关的属性的插值时,要先在三维空间中计算,再投影到二维空间。
5 总结
总之,着色就是计算模型上每一个点应该被我们看到的颜色,根据着色频率的不同,着色时又分为三种着色策略:
- Flat shading
- Gouraud shading
- Phong shading
下面是这三种着色策略的对比,可以看出,当模型片面不够多时,Flat shading的效果较差,但随着模型复杂度的提升,Flat shading的效果并不差,并且由于不需要插值运算,当模型足够精细时,使用Flat shading是性价比更高的。
