深度缓冲(Z-Buffer)
到上一篇文章为止,我们基本完成了把三维物体画在二维屏幕上的过程,但在这个过程中,还有一个非常重要的问题没有讨论,那就是在光栅化的时候我们之前的推导都没有考虑Z轴,也就是没有考虑三维物体离我们的远近,但是现实生活中我们看一个三维物体或者场景,由于物体离我们眼睛的距离不同,自然会产生遮挡现象。
比如一个立方体,在这样的视角下我们是看不到它的左平面、下平面和后平面的,但是在光栅化的过程中,我们依然会取这个立方体左平面上的三个点组成三角形并画在屏幕上,如果不考虑遮挡关系,那画出来的正方体显然和我们看到的就不一样了。
那如何在光栅化过程中考虑这种遮挡关系,并把这种关系正确的画出来呢?这就是这一节要讨论的内容。
在开始之前,要先明确一个概念,这一节所说的 Z ,并不是物体的 Z 坐标,而是代表物体离我们的远近,也就是深度,这个深度永远是正数,而且数值越小离我们越近。因为之前说了相机指向 -Z 方向,所以如果是 Z 坐标的话,离我们越近的反而数值上越大,这不符合我们的直觉。因此需要重新给出这个深度的概念。
1 画家算法
画家算法指的是我们像画家画画一样,从远处往近处画,这样近处的画面自然会遮挡住远处的画面,光栅化的时候也可以这样,我们先对三角形的深度排序,然后从远往近画在屏幕上。
但是这样的算法无法解决下面这种情况:
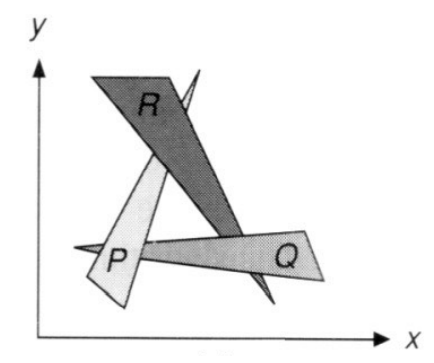
三角形的遮挡关系往往没有那么简单,因此画家算法大多情况下并不适用。
2 Z-Buffer
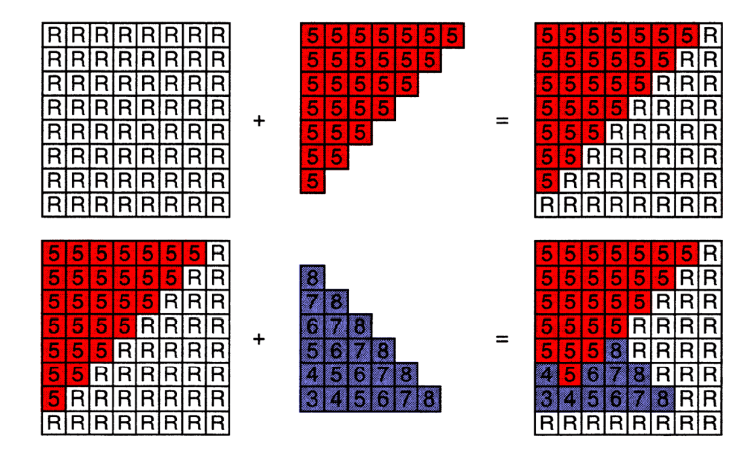
Z-Buffer的思想非常简单,那就是我们在渲染图形时,除了维护frame-buffer(显示在屏幕上的图)外,再维护一个Z-buffer(深度图),Z-buffer中存储屏幕上每一个像素当前的最小深度,在光栅化开始时,Z-buffer中每一个像素的深度都设为无穷大,之后渲染三角形的时候,每次都先判断当前渲染的三角形的深度和Z-buffer中当前像素的深度谁更小(谁离我们更近),如果三角形的深度更小,那么就把三角形的颜色存入frame-buffer中这个像素的位置,同时把Z-buffer中当前像素的最小深度更新一次,这样我们总能保证深度小的颜色遮挡深度大的颜色。
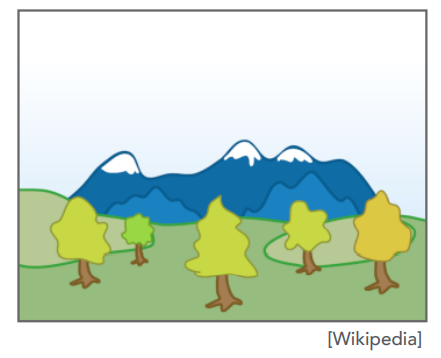
Z-buffer和frame-buffer总是同时渲染的,因此当我们生成一张图片的时候,也就生成了这张图片的深度图。

可以看到深度图中越远的地方像素值越大,越近的地方像素值越小。
Z-buffer的伪代码如下:

相比于画家算法 O(nlogn) ,Z-buffer只需要 O(n) 的时间复杂度。
为什么是O(n)?
假设每个三角形只覆盖常数个像素,那么Z-buffer做的就是对每一个三角形判断对应的深度,然后填充像素,因此只需要花费 O(1) 时间,那么有n个三角形,复杂度就是O(n).
最后说一下Z-buffer的优势,就是与画三角形的顺序无关,只要维护对了深度信息,画出来的一定是正确是遮挡关系,并且对硬件没有特殊需求,容易实现。