光栅化(Rasteriztion)
首先回顾一下MVP变换的过程(之前的文章中没有提到坐标系的概念,这里回顾的时候顺便提一下图形学中的各个坐标系的转换,其实就是之前的各种变换):
- 为了得到从某一个视角看到的物体的样子,我们首先要对相机和物体进行相机变换(View / Camera Transformation),将相机的三个方向轴与世界坐标系对齐,并移到坐标原点(这一步是将相机坐标系转换到世界坐标系,或者反着说,将世界坐标系转到相机坐标系,因为相机就是我们的眼睛,是观察物体的坐标系)
- 然后对物体做同样的变换以使得相机和物体不发生相对运动
- 最后进行投影变换,无论是正交投影还是透视投影,最终物体都被投影到一个单位立方体中(这个过程是从相机坐标系到透视坐标系的过程)
接下来的问题就是如何将这个投影绘制在屏幕上,形成图形,这个过程就是光栅化的过程。
1 屏幕的定义
屏幕可以看作是一个二维矩阵,矩阵中的每一个元素存储的是像素值,屏幕显示图形的过程,就是遍历整个数组,显示对应像素值的过程。这个二维数组的大小也就是常说的分辨率。
为了简化后面的推导,这里我们把每一个像素简单的抽象成为一个方格,并且这个方格中的颜色是一致的,如下图所示:
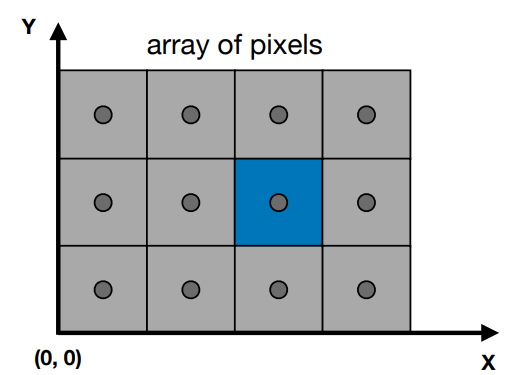
蓝色像素的坐标是 (2, 1) ,这个像素的中心点的坐标是 (2.5, 1.5) ,也就是像素 (x, y) 的中心点坐标是 (x+0.5, y+0.5) .
这里的屏幕坐标系原点定义在了左下角,通常计算机中屏幕原点在左上角,这个定义不影响后面的推导。
2 视口变换
有了屏幕的定义,我们想要把投影后的立方体显示在屏幕上,接下来要做的一步叫做视口变换,也就是将立方体转换到屏幕空间中,只有先转换到屏幕空间中,才能进一步计算屏幕空间中的点(像素)都应该是什么颜色。
这是一个3D空间到2D空间的转换,因此我们先考虑简化的情况,也就是不考虑Z方向,即不考虑3D空间中的远近、遮挡等关系,先只将XY平面转换到屏幕平面上,这个过程很简单,只要将立方体的XY平面映射到和屏幕一样的比例就可以。也就是把 [-1, 1] 映射到 [0, width] 和 [0, height]上。

同时还要进行平移,因为透视坐标系中原点是在 (0,0) 的位置,我们当然希望这个原点在屏幕的中央,而屏幕的左下角是原点,所以需要把透视坐标原点平移(width/2, height/2).
这样就完成了从透视坐标系到屏幕坐标系的转换。
3 光栅化
在介绍光栅化之前,有必要再次重申一下我们现在在干嘛。
我们的目标是把一个三维的物体显示在二维的屏幕上,那么我们首先做的就是坐标转换,之前的所有变换都是在做坐标转换,直到视口变换,我们终于完成了从三维坐标到二维坐标的映射;下一步就是计算三维物体顶点的颜色,我们得知道这个三维物体每个部分原来是什么颜色,才能把它显示在二维屏幕上,这个过程会通过UV贴图的颜色,结合光照,透明度等等,计算出模型每个顶点的具体颜色(R, G, B),这里我们先不管;最后就是在二维平面上绘制,所谓绘制也就是把这个二维平面填上颜色,前面说了,屏幕就是存储像素值的二维数组,所以绘制也就是计算每一个像素的颜色,然后屏幕根据这个数组就能显示出三维场景了。
OK,光栅化就是在屏幕上填充颜色的过程,但是根据什么来填颜色呢,就根据之前计算出来的三维物体上的顶点颜色来填。我们每次从三维物体上取三个点,映射到二维空间,形成一个三角形,这个三角形的颜色取决于三个顶点的颜色,具体有几种取法:
- 三个顶点颜色取平均值
- 取某一个顶点的颜色
- 三个顶点颜色渐变
使用哪种取法可以根据实际需求来定,不是我们目前讨论的关键。
为什么是三角形?
因为三角形是最最基本的几何图形,任何多边形都可以拆分成若干三角形,并且三角形有许多优秀的性质,比如对于图形的内外有严格的定义,再比如很好进行插值运算,上面三角形颜色取三个顶点颜色的渐变就是三角形优势的体现之一。
有了这个三角形之后,我们要做的事情就很简单了,判断每一个像素是否在这个三角形内部,如果在内部,就填上三角形的颜色。
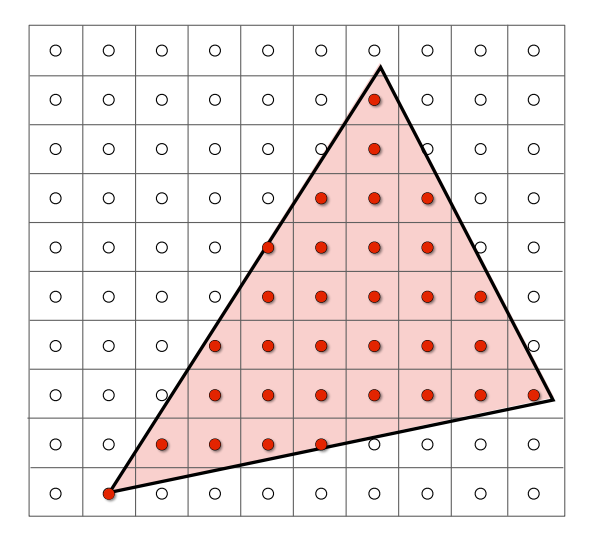
这个过程其实是一个采样的过程,采样这个概念非常重要,简单而不严谨的来说就是定义一个函数,计算每个采样点在这个函数上的值就是采样。这里的函数就是判断一个点 (x, y) 是否在给定的三角形内部,那么如何实现这个函数的功能呢?
最简单的方法就是向量叉乘,如下图所示:
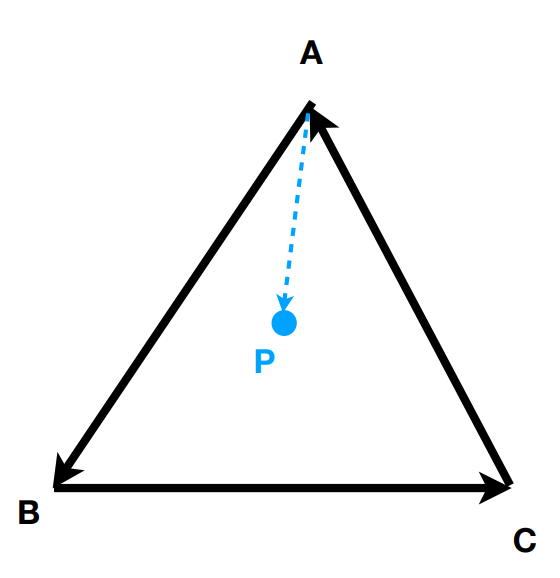
对于点 P,计算向量$\vec{AB}$与向量$\vec{AP}$的叉乘,得到的方向朝向屏幕外,这意味着点 P 在 AB 的左边,同理计算向量$\vec{BC}$与向量$\vec{BP}$的叉乘,得到的向量方向也是朝向屏幕外,这意味着点 P 在 BC 的左边,同样计算向量$\vec{CA}$与向量$\vec{CP}$的叉乘,得到的向量方向还是朝向屏幕外,这意味着点 P 在 CA 的左边,于是我们可以判定点 P 在三角形 ABC 的内部。
如果三个叉乘得到的某一个向量方向朝屏幕内,就说明点 P 在某一条边的右侧,那么点 P 一定在三角形ABC外部。这里给出C++版本代码:
1 | /* |
利用这个方法就可以判断任意一个点是否在三角形内部了,当然还可以算出三条边的方程,带入 P 点坐标得到三个值,判断同号异号,本质上和向量叉乘是一样的。
如果一个点在三角形边缘怎么算?
这个可以根据需求自己规定,而且几乎所有的图形API,比如OpenGL、DirectX都对这种情况有明确的规定,无需担心。
到此我们其实就完成了光栅化的过程。总结一下:
- 取三个点构成三角形并计算三角形颜色
- 判断屏幕上每一个像素是否在三角形内部,在则上色
这个过程很简单,但存在许多问题,比如按照上面的流程,我们的代码应该这样写:
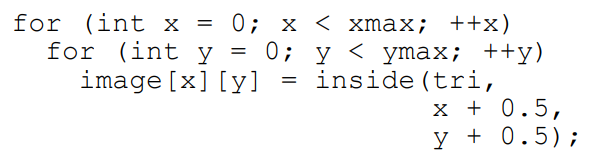
显然十分暴力,对于下大多数情况来说,我们完全不必遍历所有像素点,使用一个Bounding Box就可以大幅降低时间复杂度:
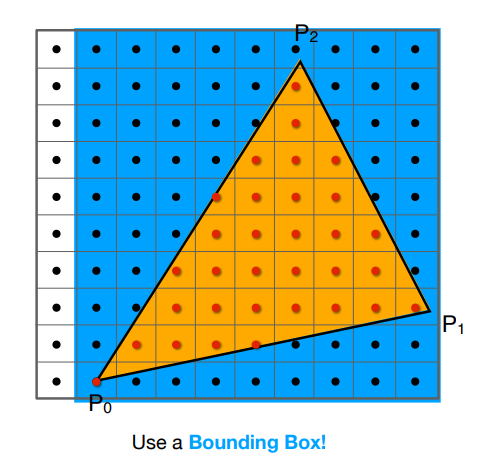
但这还不够,如果三角形非常细长,而且还刚好倾斜45°左右,那么实际上它也只占整个Bounding Box很少一部分,于是我们可以进一步改进:
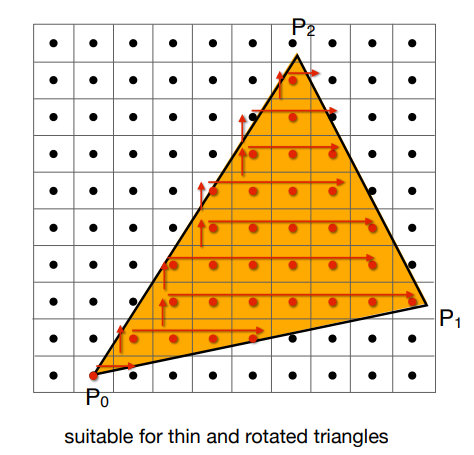
先算出每一行的起点坐标,逐行扫描,遇到不在三角形内部的点就开始扫描下一行。
现在我们来看一下光栅化之后的结果是什么样的:
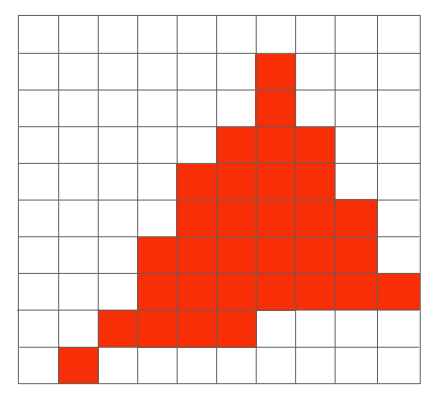
而我们想得到的样子却是这样:

不能说毫无关系,但确实不是一个东西,这是因为我们现在得到的光栅化结果有太多的锯齿了,更专业一点的说法就是我们的光栅化过程使得图形走样(Aliasing)了,因此我们必须对光栅化的过程进行抗锯齿,更准确的说法叫做反走样。关于反走样将在下一篇文章中进行详细介绍。